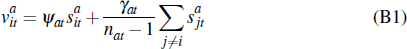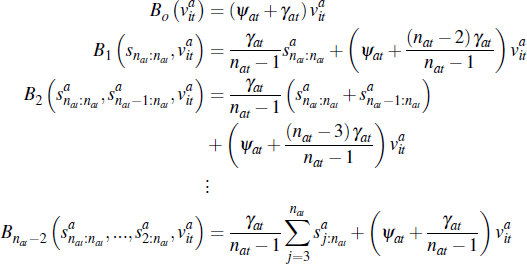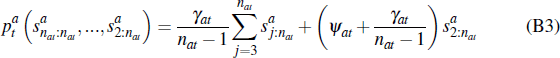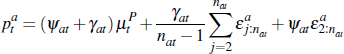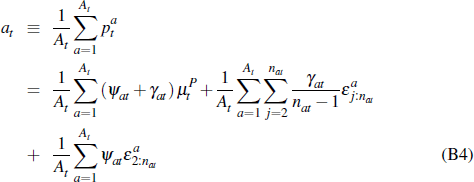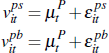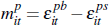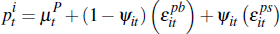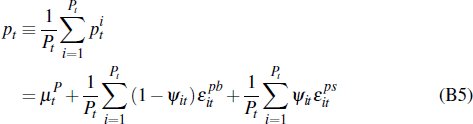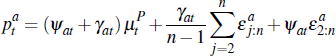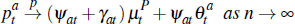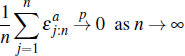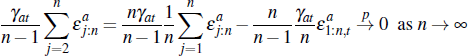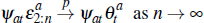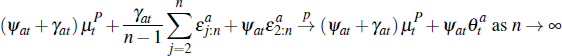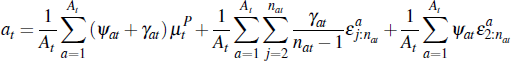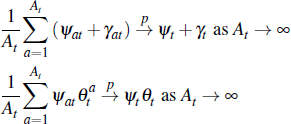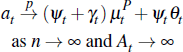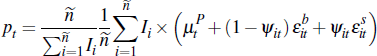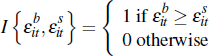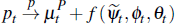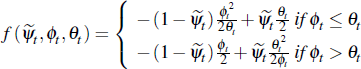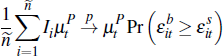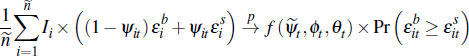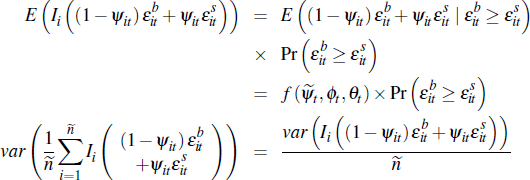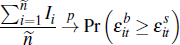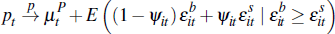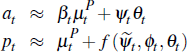RDP 2014-09: Predicting Dwelling Prices with Consideration of the Sales Mechanism Appendix B: A Theoretical Example
September 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 822KB
B.1 Auction Prices
For the auction price mechanism, we use a linear example of an affiliated values auction as discussed by Milgrom and Weber (1982) and Klemperer (1999). We assume each time period (quarter) t that multiple English auctions occur. Each auction (indexed by dwelling a at time t) has nat risk-neutral bidders (hereafter buyers). Buyers' valuations are given by:
where 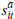 is buyer i's private signal (estimate) of the worth of dwelling a
in quarter t, and ψat ≥ 0 is the weight
attached to a buyer's own signal and γat >
0 is the weight attached to the mean of other buyers' signals.
is buyer i's private signal (estimate) of the worth of dwelling a
in quarter t, and ψat ≥ 0 is the weight
attached to a buyer's own signal and γat >
0 is the weight attached to the mean of other buyers' signals.
We assume that each buyers' own estimate of the worth of dwelling a in period t is given by a common component, 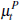 and an idiosyncratic
component
and an idiosyncratic
component 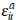 :
:
We assume that 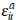 is uniformly distributed with support
is uniformly distributed with support 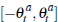 .
.
We assume buyers participate in an ascending bids English auction – the mechanism commonly used to sell dwellings in Australia – and we abstract from the possibility that sellers can post a reserve price.[28]
A bidding strategy is given by the prices at which buyers are no longer willing to remain in the auction. The following bidding strategy is consistent with a symmetric equilibrium:
where 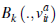 represents the price at which a buyer with valuation
represents the price at which a buyer with valuation 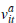 drops out given that
k players have previously dropped out of the auction, and
drops out given that
k players have previously dropped out of the auction, and 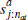 is the jth
highest signal of the value of dwelling a in period t (and
so
is the jth
highest signal of the value of dwelling a in period t (and
so 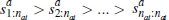 ).
Note that in this equilibrium other buyers' signals can be inferred as
they exit the auction. That is, information about the value of the dwelling
is revealed through the auction process.
).
Note that in this equilibrium other buyers' signals can be inferred as
they exit the auction. That is, information about the value of the dwelling
is revealed through the auction process.
That this is a symmetric equilibrium bidding strategy can be checked by noting that
all of the above exit points occur when the buyer with valuation 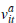 is indifferent to exiting and remaining in the auction, given the observed exit
of k players previously.
is indifferent to exiting and remaining in the auction, given the observed exit
of k players previously.
The equilibrium sale price in this auction is given by the point at which the second-last buyer drops out of the auction, and so there is only one remaining buyer:
Using Equation (B2) we can rewrite Equation (B3) as:
where 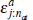 is the jth highest idiosyncratic component of the estimate of dwelling
a's value in period t.
is the jth highest idiosyncratic component of the estimate of dwelling
a's value in period t.
Taking an average price of all auctions that occurred in period (quarter) t, we have:
where At is the total number of successful auctions that occurred.
B.2 Private-treaty Prices
We now model price determination in private-treaty negotiations. In particular, we assume that the bilateral negotiation between a buyer and seller is consistent with a Nash bargaining outcome. We assume a single buyer and seller who have valuations for dwelling i in quarter t of:
where idiosyncratic components are drawn randomly from uniform distributions on the
intervals 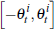 and
and 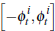 respectively. Again,
respectively. Again, 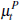 is the common valuation of the dwelling.
is the common valuation of the dwelling.
A valid sale requires 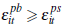 (we have a valid match) and the match surplus is given by:
(we have a valid match) and the match surplus is given by:
With Nash bargaining the negotiated private-treaty sale price is:
where ψit ∈ [0,1] is the bargaining weight of the buyer and (1– ψit ) is the bargaining weight of the seller.
The average private-treaty sale price given Pt successful private-treaty sales in a quarter will be:
B.3 An Unobserved Components Representation
To link the theoretical models to our empirical findings, we first show that average auction and private-treaty prices admit an unobserved components representation. We then show, given certain restrictions, this unobserved components representation admits a VECM representation with finite lags.
To derive the unobserved components representation of average auction and private-treaty prices, we take asymptotic approximations of each average price. For auctions, we take the approximation as both the number of buyers in each auction and the overall number of auction transactions become large. For private-treaty prices, the approximation is taken as the number of overall private-treaty negotiations (which includes successful and unsuccessful negotiations) becomes large.
B.3.1 Auction prices
Recall that 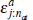 is the jth highest order statistic after nat random
draws from a uniform distribution with support
is the jth highest order statistic after nat random
draws from a uniform distribution with support 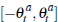 . To conserve notation,
we will assume nat = n for all a and
t, without loss of generality. We first discuss convergence of an
indiviudal auction price, as n →∞, and then convergence
of the average auction price as the number of auctions grows large (approaches
infinity).
. To conserve notation,
we will assume nat = n for all a and
t, without loss of generality. We first discuss convergence of an
indiviudal auction price, as n →∞, and then convergence
of the average auction price as the number of auctions grows large (approaches
infinity).
The equilibrium price for auction a at time t is given by:
Lemma 1. An individual auction converges to a weighted sum of the common component of valuations and the upper bound from which idiosyncratic signals are drawn. That is:
Proof. We begin studying the convergence of the term 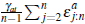 . First, note that:
. First, note that:
And so:
Next note that:
Finally, since ψat, γat and 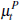 are not functions
of n, we obtain
are not functions
of n, we obtain
as required.
Turning to average prices, the average auction price is:
We study convergence of the average price as At → ∞; that is, the number of auctions is large. Applying the previous results and assuming that:
it is straightforward to verify:
B.3.2 Private-treaty prices
We next study the convergence of private-treaty prices as the number of bilateral
negotiations becomes large. Let 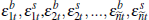 be
be 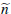 pairs of random draws with each buyer draw from a uniform distribution with support
pairs of random draws with each buyer draw from a uniform distribution with support
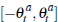 and each seller draw is from a uniform distribution with support
and each seller draw is from a uniform distribution with support 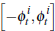 , where
, where 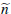 now refers to the
total number of private-treaty negotiations, including those that are successful
and those that are not. The average private-treaty price, based on successful
transactions, is:
now refers to the
total number of private-treaty negotiations, including those that are successful
and those that are not. The average private-treaty price, based on successful
transactions, is:
where 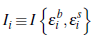 is an indicator function used to identify successful sales:
is an indicator function used to identify successful sales:
We are interested in the convergence of pt as 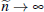 . That is, as the number of negotiations
becomes very large.
. That is, as the number of negotiations
becomes very large.
Lemma 2. Average private-treaty prices converge to a mixture of common and idiosyncratic components. The idiosyncratic components are a non-linear function of the dispersion of buyers and sellers, and the Nash bargaining parameter. Formally:
where
Proof. First notice that:
It is straightforward to show:
This follows since:
where 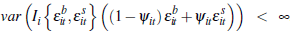 .
We have assumed
.
We have assumed 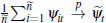 (note ψit is statistically
independent of the signals
(note ψit is statistically
independent of the signals 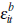 and
and 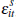 ) and applied Chebyshev's
inequality.
) and applied Chebyshev's
inequality.
Next note:
Bringing these results together and applying Slutsky's theorem:
where the final term is simply given by 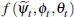 as required.
as required.
B.3.3 Summary of results
In sum, we have established that average auction and private-treaty prices can be approximated in large samples using the unobserved components model:
where 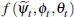 is defined in Lemma 2 and we define βt = ψt
+ γt.
is defined in Lemma 2 and we define βt = ψt
+ γt.
Footnote
See Appendix D for the inclusion of seller reserve prices. [28]