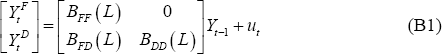RDP 2014-11: Exchange Rate Movements and the Australian Economy Appendix B: Estimation and Identification

To recover the structural shocks in Equation (1), we estimate the reduced form equation:

Where 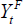is a vector of foreign variables, 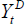is a vector of domestic variables and 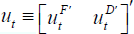is a vector of potentially correlated reduced form shocks with a variance-covariance matrix Σ.

The matrix Σ and the structural variance-covariance matrix, Ω, are related according to:

To identify the structural shocks, we need to place at least n(n − 1)/2 restrictions on the form of Ω and A, where n is the number of variables included in each VAR. We identify one structural shock – an exchange rate shock – and identify this shock using a recursive ordering. Specifically, we assume that the exchange rate responds to all other shocks contemporaneously but that exchange rate shocks affect other variables with a lag. To implement this identification, we assume that A is lower triangular and take a Choleski decomposition of Σ, ordering the exchange rate shock last.