RDP 2014-11: Exchange Rate Movements and the Australian Economy 2. Model and Data

This section outlines the statistical model that we use to examine exchange rate shocks and describes the data.

2.1 The VAR Model

We use the following VAR framework throughout our analysis. Let 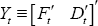be a vector of foreign (F_t) and Australian (D_t) economic variables. We are interested in analysing the structural VAR:

Where the matrix A summarises the contemporaneous relationships between the variables, Ã(L) is an autoregressive lag polynomial of order L and ε_t is a vector of independently and identically distributed structural shocks with a variance-covariance matrix Ω. Consistent with the small open economy assumption typically used in studies of the Australian economy, we restrict the parameters of A and Ã(L) so that Australian economic developments do not affect foreign variables either contemporaneously or with a lag.

We identify exchange rate shocks using a recursive ordering approach. Specifically, we identify an exchange rate shock as any movement in the real exchange rate that is not explained by changes in other macroeconomic variables.^[1]

This identification rests on two assumptions. First, that macroeconomic shocks affect the real exchange rate immediately. Second, that exchange rate shocks affect other macroeconomic variables with a lag. To justify the first assumption, we note that short-term movements in the real exchange rate largely reflect changes in nominal exchange rates. The Australian dollar floats freely and its nominal value is determined in highly liquid foreign exchange markets. Hence, its value can adjust rapidly to incorporate changes in macroeconomic fundamentals. The second assumption is consistent with the idea that it takes time for firms to alter pricing and production decisions in response to changed monetary conditions, including changes in exchange rate levels. At first glance, the case for a delayed monetary policy response to exchange rate movements might seem less plausible as movements in exchange rates are readily observable. However, numerous empirical studies have found that, in practice, exchange rate movements do not appear to have a large direct influence on monetary policy decisions in Australia (Lubik and Schorfheide 2007; Kam, Lees and Liu 2009).^[2] In Section 5 we demonstrate that our results are insensitive to the ordering of the exchange rate and interest rate variables in the VAR.

2.2 The Data

We estimate the model using seasonally adjusted data at quarterly frequencies for the period 1985:Q1 to 2013:Q2. The model includes two foreign and five domestic variables. The foreign variables are US real GDP and the Australian terms of trade.^[3] The Australian variables are real GDP, a measure of sectoral production (for example, manufacturing gross value added), trimmed mean inflation, the cash rate and the real TWI.^[4] We estimate a separate VAR for each sector of the Australian economy, as well as an aggregate model that excludes sectoral production measures.^[5]

The inclusion of output, inflation, interest rates and the real exchange rate in the domestic block is standard. For the international block, there are many additional variables that one ideally might like to include, such as foreign interest rates and inflation. Our choice of variables reflects a trade-off between including a sufficient number of variables to account for the major foreign influences on the exchange rate and a need to construct a parsimonious model given the relatively small number of observations available to us.

In the model, US output is intended to capture the impact of economic conditions in advanced economies on Australia. For the first half of our sample the US and Australian business cycles moved together closely, although the relationship has become less pronounced over the past decade (Beechey et al 2000).^[6] As well as the demand-side effects of foreign economic growth, US output also has a strong relationship with US monetary conditions, which may influence the value of Australia's real exchange rate through an uncovered interest rate parity relationship. We later show that our results are little changed when US output is replaced with major trading partner GDP.

We include the terms of trade to capture the impact of the prices of commodities, which account for a large proportion of Australia's exports, on the Australian economy. In addition, this variable may also account for some of the influence of economic conditions in emerging economies, especially China, which are significant commodity importers, on demand for Australian exports. Historically, there has been a close relationship between the level of Australia's terms of trade and the real exchange rate (Blundell-Wignall, Fahrer and Heath 1993; Gruen and Wilkinson 1994; Chen and Rogoff 2003; Stevens 2013). Failing to control for this relationship could lead us to mistakenly attribute the impact of commodity price movements to pure exchange rate shocks.

In the model, GDP and its components enter in log deviations from a quadratic trend.^[7] Inflation enters the model in quarterly percentage changes, the cash rate enters in levels, and the terms of trade and the real exchange rate enter in log levels. The specification of GDP and inflation are consistent with standard models in which monetary policymakers adjust interest rate settings in response to the output gap and deviations of inflation from its target level. Based on lag order selection tests, we include two lags of the endogenous variables in our VAR.

In Section 5 we demonstrate that our results are robust to alternative assumptions about VAR ordering, trends, lag lengths and dummy variables.

Footnotes

More formally, we identify exchange rate shocks by taking a Choleski decomposition of the variance-covariance matrix of the reduced form representation of Equation (1). Appendix B contains the technical details of our econometric approach and identification strategy. This is the same identification strategy used by Karagedikli et al (2013). [1]

Exchange rate movements may still have an indirect effect on monetary policy settings through their effect on inflation and output. [2]

We treat the terms of trade as a foreign variable because Australia is a price-taker in most export markets. Consequently, movements in the terms of trade largely reflect global rather than Australian prices. [3]

This choice of variables is similar to that of other Australian structural VARs, including Berkelmans (2005) and Lawson and Rees (2008). It is more parsimonious than Dungey and Pagan (2009), who include additional variables such as share prices. In the disaggregated models, our measure of aggregate output is real GDP less the gross value added of the industry that we include in each model. [4]

We include a dummy variable in all equations for the period 1993:Q1 to 2013:Q2 to account for the structural break in the monetary policy regime in Australia associated with the start of inflation targeting. We also include dummy variables for each of the four quarters starting with 2008:Q4 to control for the unusual period of financial market volatility associated with the global financial crisis. [5]

See Otto, Voss and Willard (2001) for a discussion of the causes and patterns of business cycle correlations amongst advanced economies. [6]

The quadratic trend helps to account for a decrease in the average pace of economic growth in the United States since the turn of the century. The results are almost identical if we use a linear trend for the GDP variables rather than a quadratic trend. [7]