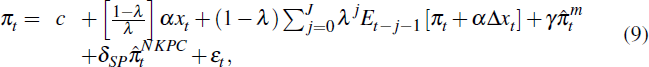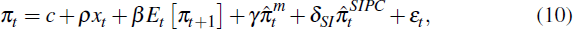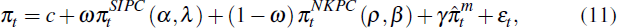RDP 2015-04: The Sticky Information Phillips Curve: Evidence for Australia 4. Results
April 2015 – ISSN 1448-5109 (Online)
- Download the Paper 738KB
4.1 Low-inflation Period
Table 3 reports estimates for the SIPC over the 1995–2013 period. Using RBA and Consensus forecasts for CPI inflation yields a negative estimate for λ, contradicting the SIPC model, which requires the degree of information rigidity to be between zero and one. There is no evidence of information rigidity, largely because CPI inflation over the low-inflation period has been dominated by idiosyncratic shocks, rather than inertial monetary policy shocks. Some of the evidence against a high degree of information rigidity comes from the tax changes associated with the introduction of the GST. The sharp rise and fall in CPI inflation was accurately incorporated into real-time RBA and Consensus forecasts, which is inconsistent with the inertial dynamics implied by a high degree of information rigidity. Much of the explained variation in CPI inflation for these SIPC equations is accounted for by the 1999/2000 period. For both the RBA and Consensus forecast versions of the SIPC, the estimated degree of real rigidity is very high, indicated by a small estimate for α.
| CPI inflation | Underlying inflation | |||||
|---|---|---|---|---|---|---|
| RBA | Consensus | Econometric | RBA | Econometric | ||
| Constant: c | 0.05 (0.06) |
−0.03 (0.05) |
0.47 (0.16) |
0.40 (0.10) |
0.38 (0.10) |
|
| [–1.49, 1.76] | [–0.51, 1.16] | |||||
| Real rigidity: α | −0.01 (0.03) |
0.02 (0.04) |
−0.58 (1.07) |
−0.02 (0.16) |
−0.30 (0.24) |
|
| [–5.03, 1.47] | [–1.09, 0.29] | |||||
| Information rigidity: λ | −0.45 (0.10) |
−0.18 (0.22) |
0.93 (0.07) |
0.87 (0.05) |
0.86 (0.06) |
|
| [–0.36, 1.75] | [–0.84, 2.04] | |||||
| Import prices: γ ×10 | −0.16 (0.09) |
−0.10 (0.12) |
−0.05 (0.11) |
0.07 (0.04) |
0.08 (0.05) |
|
| [–0.38, 0.15] | [–0.12, 0.18] | |||||
| Durbin-Watson | 1.63 | 1.77 | 1.75 | 1.30 | 1.30 | |
| R2 | 0.63 | 0.58 | 0.03 | 0.12 | 0.11 | |
| Impose α = 0.1 | ||||||
| Constant: c | −0.06 (0.07) |
−0.06 (0.10) |
0.51 (0.18) |
0.35 (0.11) |
0.39 (0.13) |
|
| [–1.13, 1.93] | [–0.84, 1.41] | |||||
| Information rigidity: λ | 0.25 (0.27) |
0.43 (0.21) |
0.94 (0.08) |
0.87 (0.06) |
0.87 (0.08) |
|
| [0.28, 1.41] | [–0.13, 1.46] | |||||
| Import prices: γ ×10 | −0.01 (0.17) |
0.02 (0.14) |
−0.03 (0.01) |
0.07 (0.04) |
0.11 (0.00) |
|
| [–0.31, 0.15] | [–0.02, 0.19] | |||||
| Durbin-Watson | 1.38 | 1.28 | 1.72 | 1.27 | 1.23 | |
| R2 | 0.36 | 0.42 | 0.01 | 0.11 | 0.07 | |
| Notes: Newey-West standard errors are reported in parentheses; where forecast series have been estimated, a 95 per cent bootstrap confidence interval is reported in brackets | ||||||
Using the econometric forecasts, which abstract from tax changes, the estimated SIPC indicates a high degree of information rigidity. But the estimated degree of real rigidity is negative, contradicting the assumption that α > 0. Furthermore, the amount of the variation in CPI inflation explained by the SIPC is negligible. For SIPC estimates using the econometric forecasts, bootstrap standard errors taking forecast uncertainty into account are reported in brackets and, as with the estimates using RBA and Consensus forecasts, ordinary standard errors are reported in parentheses. See Appendix A for details on the construction of the bootstrap standard errors. In general, the bootstrap standard errors are about an order of magnitude larger than the ordinary standard errors, indicating that the estimated parameters are sensitive to the forecasts.
The estimated SIPC for underlying inflation, using RBA and econometric forecasts, yields an estimated degree of information rigidity implying that firms on average update their information sets about once every seven quarters. Underlying inflation measures remove much of the idiosyncratic variability from CPI inflation, resulting in relatively inertial series that are more consistent with a high degree of information rigidity. However, the estimated degree of real rigidity using the underlying inflation measure remains theoretically inconsistent, and the proportion of variation in underlying inflation explained by the SIPC is modest.
The real rigidity estimates can in part be explained by the small contemporaneous correlation between quarterly inflation and the output gap over the low-inflation period, which implies that the term α [(1−λ)/λ] in Equation (2) is small. If the estimated degree of information rigidity is small (λ is close to zero), then the estimated degree of real rigidity must be high (α close to zero). This is the case for the CPI inflation SIPC using RBA and Consensus forecasts. In contrast, if the estimated degree of information rigidity is large, then the term (1−λ)/λ is small, and the degree of real rigidity is imprecisely estimated, as is the case for the SIPC estimated with underlying inflation.[7]
To the extent that weak identification affects the estimated output-inflation trade-off, imposing the degree of real rigidity may yield more accurate estimates of the degree of information rigidity. The bottom panel in Table 3 reports SIPC estimates imposing α = 0.1, the degree of real rigidity conjectured by Mankiw and Reis (2002). The estimated degree of information rigidity for the underlying inflation SIPC, and the CPI inflation SIPC using econometric forecasts, are largely unaffected by the imposition of α = 0.1. This is because the freely-estimated versions of these equations yielded a large estimate for λ, in which case the degree of real rigidity is imprecisely estimated. But for the CPI inflation SIPC estimates using RBA and Consensus forecasts, imposing the value of α has a substantial effect on the estimated degree of information rigidity. The estimated value of λ turns positive, and indicates that firms on average update their information sets about once every 1–2 quarters. But by making inflation more inertial, the rise in λ substantially worsens the fit of the model, indicated by the decline in the R-squared statistic when α = 0.1 is imposed.
4.2 Long Sample
The estimates presented thus far exclude the early 1990s disinflation. But an appealing theoretical aspect of the SIPC is its ability to generate costly disinflations, in contrast to the sticky-price model. In fact, Ball (1994) shows that the NKPC predicts a boom in output upon announcement of a credible disinflation. This occurs because firms that are able to adjust their price reset according to the expected new lower level of inflation, raising the real value of money holdings, and stimulating demand (Mankiw 2001). In practice, disinflations are typically contractionary.[8] Including the disinflationary period in the estimation period may improve identification of the SIPC model parameters, and provides a potentially informative sample period to distinguish between the sticky-price and sticky-information models.
Table 4 reports estimates of the SIPC using data for the period 1980–2013, over which only the econometric forecasts are available; estimates are presented for truncation of the SIPC at both a one- and two-year horizon.[9] In each case, the estimated degree of information rigidity is theoretically consistent. For CPI inflation, the estimated values for λ indicate that firms on average update their information set each 3–5 quarters. The estimated degree of information rigidity is larger over the 1980–2013 sample than the 1995–2013 sample largely because CPI inflation behaved inertially during the 1980s and the period of disinflation, which is consistent with the SIPC model. But despite the inertial behaviour of underlying inflation over the 1980–2013 period, the estimated degree of information rigidity is relatively low. This is because the long-horizon underlying inflation forecasts substantially overpredicted inflation during the disinflation (see Figure 2). A high degree of information rigidity would place substantial weight on these poorly performing long-horizon forecasts, reducing the empirical fit of the SIPC.
| CPI inflation | Underlying inflation | ||||
|---|---|---|---|---|---|
| J = 4 | J = 8 | J = 4 | J = 8 | ||
| Constant: c | 0.08 (0.08) |
0.02 (0.09) |
0.00 (0.05) |
−0.06 (0.03) |
|
| [−0.29, 0.33] | [−0.37, 0.24] | [−0.17, 0.10] | [−0.13, –0.02] | ||
| Real rigidity: α | 0.06 (0.09) |
−0.04 (0.24) |
0.03 (0.04) |
0.00 (0.01) |
|
| [−3.42, 1.09] | [−1.12, 0.75] | [−1.52, 0.54] | [−0.02, 0.02] | ||
| Information rigidity: λ | 0.65 (0.07) |
0.80 (0.05) |
0.50 (0.10) |
0.11 (0.14) |
|
| [−0.52, 1.17] | [−0.07, 1.40] | [−1.18, 1.64] | [−2.02, 0.75] | ||
| Import prices: γ ×10 | 0.19 (0.12) |
0.16 (0.12) |
0.16 (0.05) |
0.18 (0.06) |
|
| [−0.19, 0.49] | [−0.22, 0.45] | [0.04, 0.26] | [−0.02, 0.32] | ||
| Durbin-Watson | 1.54 | 1.47 | 1.11 | 1.25 | |
| R2 | 0.59 | 0.58 | 0.82 | 0.82 | |
| Davidson-MacKinnon non-nested model tests | |||||
| δSI | 0.25 (0.37) |
0.14 (0.27) |
0.54 (0.56) |
1.52 (1.01) |
|
| [−0.85, 0.89] | [−0.54, 0.48] | [−0.88, 1.43] | [−8.16, 7.46] | ||
| δSP | 0.56 (0.58) |
0.79 (0.13) |
−0.10 (0.06) |
−0.10 (0.06) |
|
| [−6.67, 5.55] | [−1.36, 2.48] | [−0.30, –0.05] | [−0.29, –0.03] | ||
| Impose α = 0.1 | |||||
| Constant: c | 0.10 (0.08) |
0.03 (0.09) |
0.05 (0.06) |
−0.08 (0.04) |
|
| [−0.19, 0.33] | [−0.31, 0.26] | [−0.25, 0.19] | [−0.18, –0.05] | ||
| Information rigidity: λ | 0.66 (0.07) |
0.80 (0.05) |
0.58 (0.09) |
0.51 (0.17) |
|
| [0.15, 1.04] | [0.44, 1.05] | [−0.02, 0.98] | [−0.06, 1.00] | ||
| Import prices: γ ×10 | 0.19 (0.12) |
0.17 (0.12) |
0.15 (0.05) |
0.19 (0.08) |
|
| [−0.06, 0.40] | [−0.01, 0.03] | [0.09, 0.19] | [0.04, 0.26] | ||
| Durbin-Watson | 1.52 | 1.44 | 1.03 | 0.92 | |
| R2 | 0.59 | 0.57 | 0.81 | 0.78 | |
| Notes: Newey-West standard errors are reported in parentheses; bootstrap 95 per cent confidence intervals that account for uncertainty associated with estimation of the forecasts are reported in brackets | |||||
Because of the weak contemporaneous correlation between inflation and the output gap, the estimated degree of real rigidity is large (α is small) for all SIPC specifications reported in Table 4. Imposing the degree of real rigidity to be α = 0.1 has little effect on the estimated degree of information rigidity or the fit of the SIPC, except for the underlying inflation SIPC truncated at a two-year horizon. As explained earlier, when the freely estimated degree of information rigidity is large, the coefficient on the output gap is insensitive to the parameter α. The share of the variation in inflation explained by the SIPC is high, largely because the model captures the mean shift in the early 1990s.
4.3 Comparing the SIPC and the NKPC
For the 1980–2013 period as a whole, the SIPC appears to provide a plausible model of inflation. But is the sticky-information model a better description of inflation dynamics than the sticky-price model? Because the SIPC and NKPC models are non-nested, discriminating between the two models is not as straightforward as imposing restrictions on the estimated parameters of the SIPC. The first set of tests used to discriminate between the two price-setting models are Davidson and MacKinnon (2002) non-nested model tests. Under the null hypothesis that the sticky-information model is correct, the SIPC is augmented with NKPC fitted values and re-estimated:
where  is the fitted values from estimation of the NKPC, Equation (7). Under the null hypothesis
that the SIPC is correct, the NKPC fitted values have no additional explanatory
power for inflation, and the coefficient δSP is insignificantly
different from zero. Rejection of the hypothesis δSP
= 0 provides evidence in favour of the NKPC. Similarly, under the null hypothesis
that the sticky-price model is correct, the NKPC model is augmented with SIPC
fitted values and re-estimated:
is the fitted values from estimation of the NKPC, Equation (7). Under the null hypothesis
that the SIPC is correct, the NKPC fitted values have no additional explanatory
power for inflation, and the coefficient δSP is insignificantly
different from zero. Rejection of the hypothesis δSP
= 0 provides evidence in favour of the NKPC. Similarly, under the null hypothesis
that the sticky-price model is correct, the NKPC model is augmented with SIPC
fitted values and re-estimated:
where 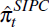 is the fitted values from estimation of the SIPC, Equation (4). Rejection of the
hypothesis δSI = 0 provides evidence in favour of
the SIPC model.
is the fitted values from estimation of the SIPC, Equation (4). Rejection of the
hypothesis δSI = 0 provides evidence in favour of
the SIPC model.
The middle panel of Table 4 reports estimates for these non-nested model tests. For each inflation measure and truncation length, we cannot reject the null hypothesis δSP = 0 in testing the null hypothesis that the SIPC is the correct model, or the hypothesis that δSI = 0 in testing the null hypothesis that the NKPC is the correct model. This is true even with ordinary standard errors, that do not allow for the fact that the forecasts are generated regressors. Thus, the Davidson and MacKinnon (2002) non-nested model tests provide inconclusive evidence.
Estimation of an encompassing model provides an alternative means to test the SIPC against the NKPC. This involves jointly estimating the parameters for each model:
where ω is the weight on the SIPC model, 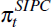 (α,
λ) is SIPC inflation, given by the right-hand-side of Equation
(4) excluding the import price term, and
(α,
λ) is SIPC inflation, given by the right-hand-side of Equation
(4) excluding the import price term, and  (ρ,β)
is NKPC inflation, given by the right-hand-side of Equation (7), excluding
the import price term. Because the encompassing regression is highly non-linear
in five parameters, the SIPC parameters are restricted to be theoretically
consistent, α > 0 and 0 < λ <
1, and the sum of the weights on the models is constrained to unity, 0 <
ω < 1.
(ρ,β)
is NKPC inflation, given by the right-hand-side of Equation (7), excluding
the import price term. Because the encompassing regression is highly non-linear
in five parameters, the SIPC parameters are restricted to be theoretically
consistent, α > 0 and 0 < λ <
1, and the sum of the weights on the models is constrained to unity, 0 <
ω < 1.
The first two columns of Table 5 report encompassing test results, for CPI and underlying inflation. The results suggest that the forward-looking NKPC is a better description of inflation dynamics over the 1980–2013 period than the SIPC model: the coefficient ω, the weight on the SIPC model relative to the NKPC model, is small. Because the estimated weight on the SIPC is small, the SIPC parameters α and λ are imprecisely estimated: as ω approaches zero, a wide range of coefficients for the SIPC fits the data almost equally well. Because the output gap enters both the SIPC and the NKPC when ω is above zero, the encompassing test cannot precisely pin down the output gap parameters α and ρ in each model: identification comes only via the non-linearity in the SIPC. This imprecision is evident for the underlying inflation encompassing model.
| Encompassing test | NKPC | Hybrid NKPC | ||||||
|---|---|---|---|---|---|---|---|---|
| CPI inflation |
Underlying inflation | CPI inflation |
Underlying inflation | CPI inflation |
Underlying inflation | |||
| J = 8 | J = 8 | |||||||
| Constant | 0.08 (0.07) |
0.05 (0.04) |
0.09 (0.07) |
0.07 (0.04) |
0.09 (0.07) |
0.06 (0.04) |
||
| [−0.15, 0.23] | [−0.04, 0.13] | [−0.15, 0.24] | [−0.08, 0.20] | [−0.12, 0.23] | [−0.07, 0.15] | |||
| α | 2.68 (204.6) |
0.75 (2.98) |
||||||
| [−∞, ∞] | [−25.28, 23.03] | |||||||
| λ | 0.95 (22.64) |
0.18 (1.14) |
||||||
| [−142.64, 112.51] | [−1.26, 1.53] | |||||||
| ρ | 0.02 (1.01) |
−0.62 (2.72) |
0.02 (0.03) |
0.00 (0.02) |
0.02 (0.03) |
0.00 (0.02) |
||
| [−2.04, 1.66] | [−2.14, 0.35] | [−0.11, 0.11] | [−0.07, 0.06] | [−0.10, 0.11] | [−0.08, 0.06] | |||
| β | 0.85 (2.71) |
0.89 (0.05) |
0.84 (0.06) |
0.90 (0.05) |
0.80 (0.16) |
0.82 (0.20) |
||
| [−6.01, 6.39] | [0.76, 0.98] | [0.61, 1.03] | [0.68, 1.03] | [0.11, 1.32] | [−0.61, 1.62] | |||
| γ × 10 | 0.12 (0.11) |
0.11 (0.04) |
0.12 (0.11) |
0.10 (0.04) |
0.12 (0.12) |
0.09 (0.04) |
||
| [−0.15, 0.36] | [0.01, 0.18] | [−0.14, 0.33] | [0.02, 0.16] | [−0.25, 0.35] | [0.03, 0.16] | |||
| ω | 0.01 (3.09) |
0.15 (0.42) |
||||||
| [−0.16, 0.11] | [−0.17, 0.41] | |||||||
| LDV | 0.05 (0.16) |
0.08 (0.18) |
||||||
| [−0.72, 0.51] | [−0.39, 0.47] | |||||||
| DW | 1.91 | 1.91 | 1.91 | 2.06 | 1.98 | 2.17 | ||
| R2 | 0.60 | 0.84 | 0.60 | 0.84 | 0.60 | 0.84 | ||
| Notes: Newey-West standard errors are reported in parentheses; bootstrap 95 per cent confidence intervals that account for uncertainty associated with estimation of the forecasts are reported in brackets; LDV denotes lagged dependent variable; DW denotes Durbin-Watson | ||||||||
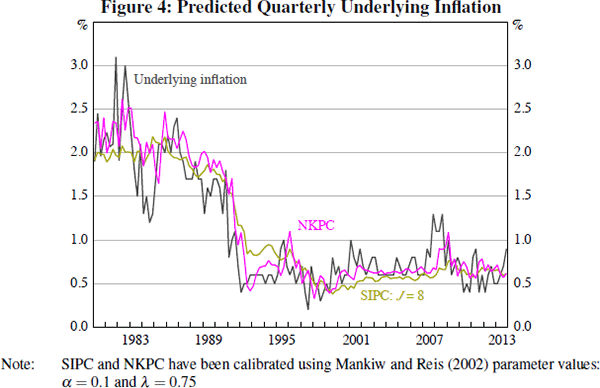
The NKPC model appears to fit the data better in part because, as shown in Figure 2, the long-horizon real-time forecasts substantially overpredicted inflation relative to the short-horizon forecasts during the early 1990s disinflation. The real-time forecast error was smaller for short-horizon forecasts because they place more weight on recent inflation outcomes and less weight on the estimated long-run mean inflation rate, which was slow to update during the disinflationary period. Thus, the SIPC model, which places weight on dated long-horizon forecasts, substantially overpredicts inflation during the disinflation, except with very low levels of information rigidity. This is particularly apparent with the calibration of the SIPC proposed by Mankiw and Reis (2002), as shown in Figure 4.
Separately estimated NKPC equations reinforce the evidence in favour of the sticky-price model. The estimated coefficient on forward-looking NKPC inflation is similar in the encompassing model and the NKPC model, and the fit of the NKPC model for CPI and underlying inflation is no worse than the encompassing model (see Table 5). The hybrid NKPC model augments the NKPC with a lagged dependent variable, providing a reduced-form means of capturing the inflation inertia that the SIPC builds in from microfoundations. The estimated weight on lagged inflation is small, consistent with the small estimated weight on the SIPC in the encompassing model.
4.4 Adaptive Expectations Phillips Curve
The previous section sought to distinguish between the non-nested SIPC and NKPC models, the two most prominent Phillips curve models in the literature. A nested alternative to the SIPC is the adaptive expectations Phillips curve (AEPC). The SIPC model reduces to a distributed-lag AEPC under the assumption that expected inflation is equal to current inflation, and expected changes in the output gap are equal to zero. Accordingly, the SIPC can be expressed as an AEPC plus expectational deviations between the two models:
Table 6 reports parameter estimates for Equation (12). Under the null hypothesis that the SIPC is correct ϕ = 1, and under the null hypothesis that the AEPC is correct ϕ = 0. Empirically distinguishing between the two models requires the SIPC rational expectations forecasts to substantially outperform the AEPC random walk forecasts; if the rational expectations forecasts are identical to the random walk forecasts, the SIPC model is indistinguishable from a distributed-lag AEPC. Particularly over the low-inflation period, the random walk benchmark has been shown to be difficult to improve upon: Atkeson and Ohanian (2001) find that Phillips curve-based forecasts do not outperform random walk forecasts for US inflation after 1984, and Heath et al (2004) report similar evidence for Australia. This means that tests seeking to distinguish between the SIPC and AEPC models have low power. Reflecting this, the bootstrap confidence intervals for the parameter ϕ in Equation (12) are wide enough to be consistent with both the SIPC and AEPC models.
| CPI inflation | Underlying inflation | ||||
|---|---|---|---|---|---|
| J = 4 | J = 8 | J = 4 | J = 8 | ||
| Constant | 0.07 (0.07) |
0.03 (0.06) |
0.02 (0.05) |
−0.02 (0.02) |
|
| [−0.11, 0.19] | [−0.24, 0.12] | [−0.14, 0.10] | [−0.07, –0.00] | ||
| α | 0.08 (0.05) |
0.13 (0.12) |
0.01 (0.03) |
0.04 (0.02) |
|
| [−0.20, 0.30] | [−1.64, 1.08] | [−0.13, 0.09] | [−0.83, 0.34] | ||
| λ | 0.60 (0.07) |
0.74 (0.06) |
0.52 (0.10) |
0.44 (0.10) |
|
| [0.26, 0.73] | [−1.23, 0.89] | [−2.02, 2.39] | [−2.75, 2.45] | ||
| γ × 10 | 0.13 (0.12) |
0.15 (0.12) |
0.15 (0.05) |
0.12 (0.04) |
|
| [−0.30, 0.46] | [−0.31, 0.47] | [0.03, 0.30] | [−0.04, 0.25] | ||
| ϕ | 0.54 (0.18) |
0.32 (0.20) |
1.80 (0.34) |
0.22 (0.13) |
|
| [−0.28, 1.24] | [−0.93, 0.97] | [−9.90, 13.00] | [−0.18, 0.58] | ||
| Durbin-Watson | 1.88 | 1.84 | 1.20 | 2.10 | |
| R2 | 0.61 | 0.61 | 0.83 | 0.86 | |
| Notes: Newey-West standard errors are reported in parentheses; bootstrap 95 per cent confidence intervals that account for uncertainty associated with estimation of the forecasts are reported in brackets | |||||
Although the SIPC and AEPC equations have similar fit, they have different theoretical implications for the behaviour of inflation. Mankiw and Reis (2002) show that, in response to a demand shock, inflation and output overshoot in the AEPC model, but behave inertially and do not overshoot in the SIPC model. Tests based on the dynamic response to shocks may be more informative for distinguishing between the SIPC and AEPC models than fit comparisons. This is left for further work.
Footnotes
This can be seen by inspection of the standard errors for α: when the estimate for λ is close to unity, the standard errors for α are large. [7]
One reconciliation of the theory and actual experience is to question the credibility of announced disinflations. But Mankiw (2001, p C57–58) argues that this feature of the NKPC cannot be so easily squared with the data: ‘Because monetary shocks have a delayed and gradual effect on inflation, in essence we experience a credible announced disinflation every time we get a contractionary shock. Yet we do not get the boom that the model says should accompany it. This means that something is fundamentally wrong with the model’. [8]
See Appendix B for estimates over the shorter 1980–1990 sample period. [9]