RDP 2015-10: The Life of Australian Banknotes 2. Background

2.1 The Life of a Banknote

A banknote's life begins with its production (Figure 1). Once produced, banknotes are held in storage until they are issued to the public. The elapsed time between production and issuance can vary considerably depending on the volume of banknotes produced in each banknote vintage (production year) and on fluctuations in the demand for banknotes. Once issued, banknotes may spend periods of time actively circulating or being held as a store of value.

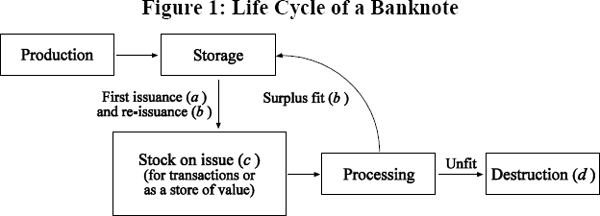
Demand for Australian banknotes broadly changes in line with the nominal growth of the economy, but also exhibits seasonal peaks in demand during December and Easter each year. Following these seasonal peaks, banknotes in excess of the general public's requirements (‘surplus fit’ banknotes) are returned to the Reserve Bank of Australia (RBA) to be reissued at a later date.

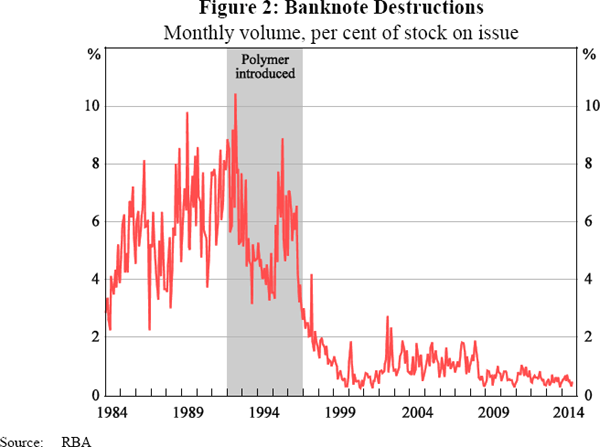
Over time, banknotes deteriorate in quality and become unfit for use in circulation. This can occur due to randomly occurring mechanical defects (including staple holes, dog-ears and tears) or gradually through the process of inkwear (where the ink wears off the banknote as a result of being handled). Banknotes returned to the RBA via the commercial cash system are assessed and validated. Fit banknotes are eventually reissued into circulation and unfit banknotes are destroyed.^[1] While the destruction of banknotes fluctuates widely from month to month, one clear trend is the large fall in the rate of destruction, from an average of 5.7 per cent of banknotes in circulation per month prior to 1992, to 1.0 per cent per month after the introduction of the polymer New Note Series (NNS) banknotes (Figure 2).

2.2 Parallels in Other Literature Areas

Examining the life of a banknote has parallels in many subject areas, including the study of the life expectancy of organisms, epidemiology, the reliability of equipment or products, and the duration of events. Each literature area draws on survival analysis as a means of exploring the proportion of a population that will survive to a particular age, the rate at which failure occurs, and the effect that different variables or treatments will have on the failure rate.^[2]

The difficulty in applying similar survival models to the study of the life of an Australian banknote is the absence of data that records a banknote's date of first issuance into circulation and date of destruction. Instead, the life of a banknote is examined through the aggregate variables commonly available to currency issuers. In Australia, stock variables include the number of banknotes on issue, banknotes that have not been previously issued and surplus fit banknotes, and flow variables include the number of banknotes issued and destroyed.

2.3 Characterising the Deterioration of Banknotes

The survival analysis literature uses specialist terms for precisely describing the duration of events, such as banknote life. These terms avoid the ambiguities that arise with everyday expressions such as ‘life’ or ‘destruction rate’. The survival function measures the probability that the terminal date (in this case, when the banknote becomes unfit and is destroyed), denoted by the random variable T, is greater than a particular time, t. For example, the probability that a $50 banknote will last at least 15 years is estimated to be around 40 per cent (see Figure 6). Formally, the survival function is given by:

The complement of the survival function is the lifetime distribution function, which measures the probability that a banknote will be destroyed before or at a particular point in time.

The derivative of the lifetime distribution function gives the event density function, which in this paper will be called the destruction function. Roughly speaking, the destruction function can be thought of as the rate at which banknotes are destroyed at a particular point in time.

The hazard function is defined as the event density at time t, given survival up to that point in time. This can be roughly interpreted as the rate at which banknotes will become unfit at a particular time, given survival up to that time. For example, 0.2 per cent of $50 banknotes that survive 20 years are then destroyed in that year.

Measures of the central tendency of a banknote's useful life, such as their mean and median life when issued, are important for decision-making and can be derived from the above functions. In particular, these measures can help to inform banknote production decisions that are typically made years in advance. It should be clear, however, that these measures of expected life at issuance are different to the mean or median age of banknotes that are currently in circulation.

2.4 The Expected Shape of Hazard Functions

A banknote's hazard function will be influenced by the two broad ways in which it can become unfit:

1. Mechanical defects are largely randomly occurring, or in other words, the probability that a banknote becomes unfit due to such a defect is invariant to the time that the banknote has been on issue. This corresponds with a constant hazard function.
2. Inkwear is a time-variant defect, since the probability that a banknote suffers sufficient levels of inkwear to be deemed unfit increases with the time spent in circulation. As such, inkwear gives rise to an increasing hazard function.

Given that these two categories of defects can occur, a banknote's hazard function is expected to increase with respect to time since first issuance.

The preceding discussion refers to the hazard function of a given banknote; however, the average hazard rate of a group of banknotes may behave differently. One important factor is heterogeneity in the use of banknotes. Even though Australian banknotes are homogeneous, in that they are all made with the same materials and production processes over time, banknotes can be used for different purposes that affect their survival characteristics. Banknotes used repeatedly for transaction purposes are likely to have relatively high hazard rates, consistent with the fact that they are likely to experience greater inkwear or be subject to a random hazard such as stapling. On the other hand, some banknotes are used as a store of value or kept for numismatic purposes, and are therefore held in a protected location where they are much less likely to suffer inkwear or a mechanical defect. Such banknotes are likely to have very low hazard rates and are unlikely to become unfit within the life of the banknote series. It is well-established in the survival analysis literature that if a population is composed of groups with differing hazard rates, even if the groups have constant or rising hazards, the aggregate hazard function could appear to be downward sloping, or rise then fall.^[3] More specific to the problem at hand, it has long been recognised in the medical literature (see Boag (1949) and Berkson and Gage (1952)) that having a proportion of long-term survivors in the population (i.e. individuals that don't suffer the event of interest within the period of study) induces a longer tail in the survival distribution and a downward bias in estimates of the aggregate hazard rate.

Another complicating factor is that the hazard rates observed by the currency issuer could be lower due to the process of detecting unfit banknotes in circulation. Unfit banknotes are predominantly detected when banknotes that are surplus to demand are returned to the commercial cash system and sorted, which means that detection rates will be affected by the rate at which banknotes return for processing. Banknotes may also continue to circulate while unfit since whether a banknote is considered no longer fit for purpose is subjective and can vary considerably from person to person.

Footnotes

For more information on the RBA's damaged banknote policy and sorting standards, see <http://banknotes.rba.gov.au/damaged-banknotes/damaged-banknotes-policy/>. [1]

This paper will refer to survival analysis; however, there are many synonyms across different fields of study. For instance, in the study of the expected length of periods of unemployment it is often referred to as duration analysis (see, for example, Lancaster (1979)). [2]

As a simple example, consider a population composed of two groups – one with a high constant hazard and one with a low constant hazard. If the two groups are not observed, on the aggregate level it will appear that the population's hazard rate is declining since the high hazard group will fail more quickly, and over time the surviving population will have a higher and higher ratio of low hazard individuals. [3]