RDP 2015-10: The Life of Australian Banknotes 3. Traditional Steady-state or Turnover Method
August 2015 – ISSN 1448-5109 (Online)
- Download the Paper 1.22MB
The most common method that currency issuers use to estimate banknote life is a simple formula: the stock of banknotes on issue (averaged over a 12-month period) relative to the total number of banknotes destroyed (in the same 12-month period). Referring to Figure 1, the formula corresponds to dividing c by d. It is commonly termed the ‘steady-state’ method since it was thought that after a banknote series had been in circulation for a number of years, the growth in banknote destructions and circulation would reach stable levels, allowing for a steady-state estimate of banknote life. The formula is analogous to a turnover rate and measures the average number of years required to replace the current stock of banknotes in circulation if the current rate of destruction continues, thus estimating the useful life of the current stock of banknotes on issue.
Table 1 shows the estimates of the average life for Australia's $5 to $50 denominations. As higher-value denominations are more likely to be used as a store of value, whereas lower-value banknotes are used more often in transactions, high-value denominations (such as the $50 or $100) turn over in the hands of the public far less frequently and hence, are expected to have longer useful lives than lower-denomination banknotes.[4] Second, the table shows that the average life of polymer banknotes has been consistently higher than that of paper banknotes. In the case of the low-value denominations, the average life of polymer banknotes is estimated at more than five years compared to less than one year for paper banknotes. In the case of the higher-value $50 denomination, the comparison is even more striking.
| Denomination | Paper | NNS polymer | |
|---|---|---|---|
| 1985–91 | Since issuance | 2000–14 | |
| $5 | 0.7 | 5.1 | 6.3 |
| $10 | 0.8 | 5.0 | 6.0 |
| $20 | 1.1 | 5.9 | 6.9 |
| $50 | 2.2 | 14.5 | 17.4 |
|
Sources: Author's calculations; RBA |
|||
The inverse of Equation (5) equals the rate that banknotes will become unfit and withdrawn in a given year, or in other words, their hazard rate. Given this method implicitly assumes that banknotes have a constant hazard rate, the median banknote life can be calculated based on the implied probabilities of survival.[5] The median is a useful measure since, compared to the mean, it will not be as affected by the long tail of the survival distribution. As expected, the median life of banknotes is consistently lower than the average for all denominations and substrates (Table 2; Figure 3).
| Denomination | Paper | NNS polymer | |
|---|---|---|---|
| 1985–91 | Since issuance | 2000–14 | |
| $5 | 0.5 | 3.5 | 4.4 |
| $10 | 0.5 | 3.5 | 4.1 |
| $20 | 0.7 | 4.1 | 4.8 |
| $50 | 1.5 | 10.0 | 12.0 |
|
Sources: Author's calculations; RBA |
|||
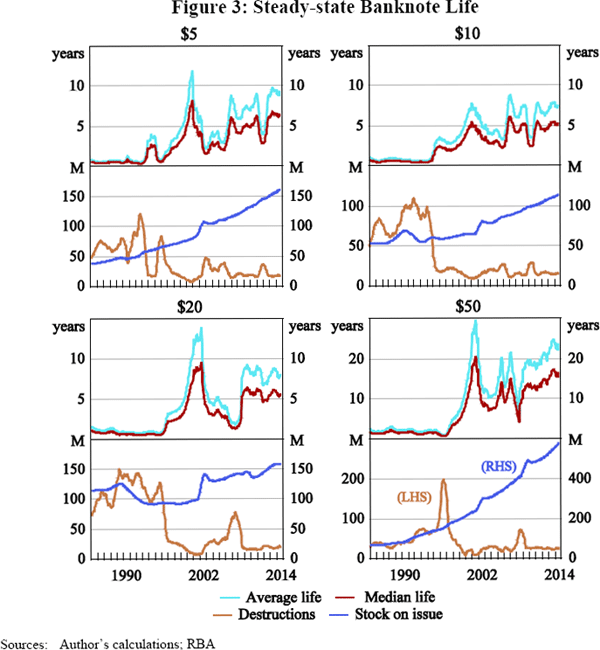
The life estimates resulting from the ‘steady-state’ formula display considerable volatility over time (Figure 3). The volatility in the estimated average life becomes more prominent as the life span of each banknote denomination becomes progressively greater than the 12-month periods included in the formula.[6] As a consequence, the estimates vary considerably over time, particularly for the larger denominations. This proposition is also supported by the contrast between the standard deviations around the mean estimates for paper and polymer banknotes (Table 3). In comparing the standard deviation of the estimated life spans of polymer banknotes since issuance to the standard deviation since 2000, it is also observed that the volatility of the estimates declines somewhat over time as the population increasingly includes banknotes across the full range of the survival distribution.
| Denomination | Paper | NNS polymer | |
|---|---|---|---|
| 1985–91 | Since issuance | 2000–14 | |
| $5 | 0.1 | 2.8 | 2.3 |
| $10 | 0.1 | 2.0 | 1.5 |
| $20 | 0.2 | 3.2 | 3.0 |
| $50 | 0.3 | 7.1 | 4.9 |
|
Sources: Author's calculations; RBA |
|||
Footnotes
Since $100 banknotes are generally held by the public as a store of value, they do not tend to actively circulate and with such little handling do not deteriorate significantly over time. Indeed, less than 10 per cent of $100 NNS banknotes ever issued have returned to the RBA as unfit banknotes. This suggests that the average life span of $100 NNS banknotes will be far longer than the NNS banknote series itself, given the decision to introduce a new banknote series in the near future. The lack of data also means that more specific estimates of the life of $100 banknotes are unreliable and have been excluded from this paper. [4]
Those familiar with survival analysis will be aware that the hazard function is constant when the survival time is exponentially distributed due to its memoryless property. [5]
To illustrate this point, consider studying a population of mice for a year. If the mice typically live for less than a year in the wild, comparing the number of deaths observed relative to the size of the population over the year may give a reasonable estimate of their average life. Now instead imagine studying a population of tortoises over a year. Since tortoises can live for more than 100 years, it may not always be accurate to estimate the average life span based on the deaths observed in one year relative to the population size. For example, if many old tortoises happened to die in a particular year, life span estimates that year are likely to be underestimated. The remaining population thereafter is much younger and therefore is likely to experience fewer deaths for a time, and so subsequent life estimates are likely to be overestimated for some time. [6]
