RDP 2015-11: Unprecedented Changes in the Terms of Trade: Online Appendix 5 The Posterior Sampler

To simulate from the joint posterior of the structural parameters and the date breaks, p(ϑ, T|Y), we use the Metropolis-Hastings algorithm following a strategy similar to Kulish et al. [2014]. As we have continuous and discrete parameters we modify the standard setup for Bayesian estimation of DSGE models. We separate the parameters into two blocks: date breaks and structural parameters. To be clear, though, the sampler delivers draws from the joint posterior of both sets of parameters.

The first block of the sampler is for the date breaks, T. As is common in the literature on structural breaks (Bai and Perron [1998]), we set the trimming parameter to 25 per cent of the sample size so that the minimum length of a segment has 20 observation. Within the feasible range we draw from a uniform proposal density and randomize which particular date break in T to update. This approach is motivated by the randomized blocking scheme developed for DSGE models in Chib and Ramamurthy [2010].

The algorithm for drawing for the date breaks block is as follows: Initial values of the date breaks, T₀, and the structural parameters, ϑ₀, are set. Then, for the j^th iteration, we proceed as follows:

1. randomly sample which date break to update from a discrete uniform distribution with support ranging from one to the total number of breaks, in our case two.
2. randomly sample the corresponding elements of the proposed date breaks, , from a discrete uniform distribution [T_mim, T_max] and set the remaining elements to their values in T_j−1
3. calculate the acceptance ratio
4. accept the proposal with probability min {, 1}, setting T_j = , or T_j−1 otherwise.

The second block of the sampler is for the n_ϑ structural parameters.^[1] It follows a similar strategy to the date-breaks-block described above – we randomize over the number and which parameters to possibly update at each iteration. The proposal density is a multivariate Student's t– distribution.^[2] Once again, for the j^th iteration we proceed as follows:

1. randomly sample the number of parameters to update from a discrete uniform distribution [1, n_ϑ]
2. randomly sample without replacement which parameters to update from a discrete uniform distribution [1, n_ϑ]
3. construct the proposed 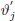by drawing the parameters to update from a multivariate Student's t– distribution with 10 degrees of freedom and with location set at the corresponding elements of ϑ_j−1, scale matrix based on the corresponding elements of the negative inverse Hessian at the posterior mode multiplied by a tuning parameter ι = 0.15.
4. calculate the acceptance ratio or set = 0 if the proposed 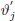includes inadmissible values (e.g. a proposed negative value for the standard deviation of a shock or autoregressive parameters above unity) preventing calculation of p(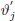, T_j|Y)
5. accept the proposal with probability min {, 1}, setting ϑ_j = 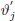, or ϑ_j−1 otherwise.

We use this multi-block algorithm to construct a chain of 575,000 draws from the joint posterior, p(ϑ, T|Y), throwing out the first 25 per cent as burn-in. Trace plots show that the sampler mixes well.

Footnotes

In our application n_ϑ = 37. [1]

The hessian of the proposal density is computed at the mode of the structural parameters. [2]