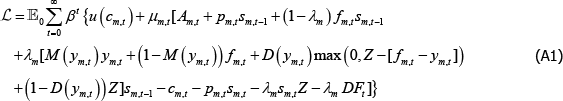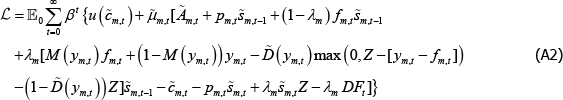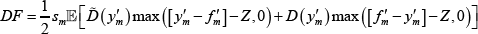RDP 2016-07: The Efficiency of Central Clearing: A Segmented Markets Approach Appendix A: Trader Behaviour and Solution Method
October 2016
- Download the Paper 2.00MB
A.1 Lagrangians
The Lagrangian for the long trader is:
where μm,t is the Lagrange multiplier on the period t budget constraint for a long trader in market m. This equation is maximised by choice of cm,t and sm,t.
The short trader is similar:
The first-order conditions from these problems yield Equations (17) and (20) in the main text.
A.2 Numerical Methods
We solve the system by first picking a scalar sm and then solving each pricing equation for a stationary price vector. Restricting attention to equilibria where the quantity of trade is not state contingent considerably simplifies the computational burden of the problem. We approximate the expectation on the right-hand side of the pricing equation using Gauss-Hermite numerical integration. The price vector is the discretised numerical approximation of the state-dependent price function. We use 35 quadrature nodes for both Am,t and ym,t, which means we have a total of 1,225 states. We use such large numbers because most of the action in our model occurs in the tails. This means that we need a large state space to ensure smooth coverage of the tails, particularly when we vary parameters like margin requirements: smaller state spaces mean that there are large discrete jumps as margin requirements or default bounds move past one of the tail quadrature nodes.
Solving the system then amounts to finding a scalar value of sm such that price vector solutions to the two pricing equations are approximately the same. We find this value of sm using a numerical nonlinear solver. In all cases we assume λm = λ for all m. This greatly simplifies the solution method, because all markets are identical. We need to solve for only one sm, because this will be a solution for all the markets.
The equilibrium solution to our model (without collateral) is always an sm
such that the price for both agents is zero. This is consistent with real-world practice: most
OTC derivatives have zero net present value when agreed on.[32] This is an intuitive
result, traders are trading the contract so that their consumption (which depends on
sm) is uncorrelated with the payoff of the contract. Because of the symmetry
in long and short traders' optimisation programs, the sm that ensures
this is the case for both traders is the same (noting that 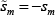 ).
).
In some cases we need to evaluate integrals across all markets, for example, for the stationary equilibrium CCP default fund fee (Equation (24)). We do so by relying on the fact that draws of ym and Am are independent of sm and that both ym and Am are independent and identically distributed and uncorrelated with other markets (i.e. corr(Am, An) = 0). These assumptions allow us to use a law of large numbers such that:
which we evaluate by a Gauss-Hermite quadrature rule in the same way as outlined above.
In principle, we can also solve for a state-contingent vector for sm, and focus on the first moment of this distribution. Numerically, this is a much more computationally demanding problem because we quickly run into the curse of dimensionality when jointly maximising welfare over λm and Z. Nevertheless, to see if our results are sensitive to our simpler solution method we compared the first moment of the solution with a given distribution for sm with the non-state-contingent solution. The results are similar in this case.
Footnote
There are a few exceptions, such as market-agreed coupon interest rate swaps and standardised credit index derivatives. [32]