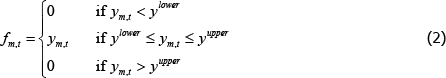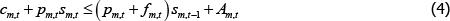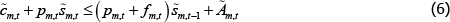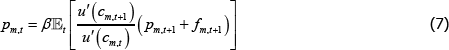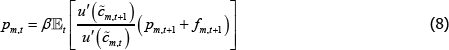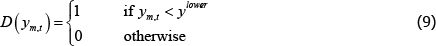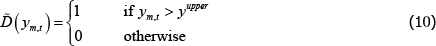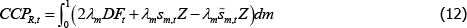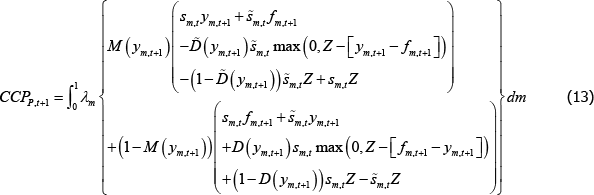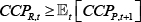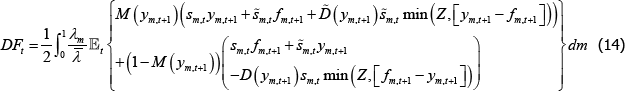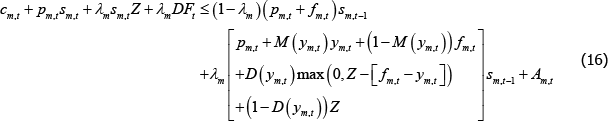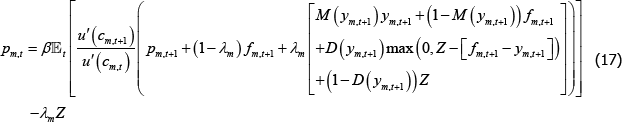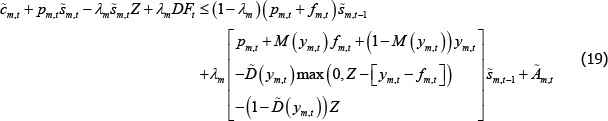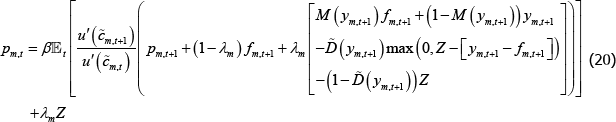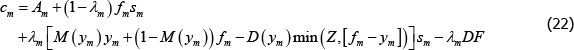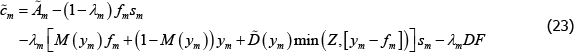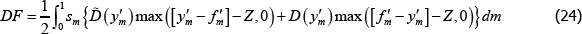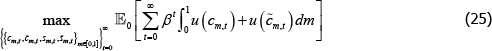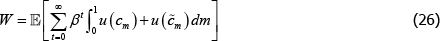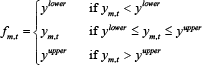RDP 2016-07: The Efficiency of Central Clearing: A Segmented Markets Approach 3. The Model
October 2016
- Download the Paper 2.00MB
We use a consumption-based asset pricing model with market segmentation, in the spirit of Edmond and Weill (2012), to study central clearing and OTC derivatives. Our core modifications are to: introduce default to provide a motive for counterparty insurance; model bilateral zero-sum financial trade explicitly; and include a modelling device for central clearing through a CCP.
In brief, our model has a continuum of markets for OTC derivatives, each of which contains two types of traders who can trade only in that market. Traders enter into OTC derivatives contracts to offset an idiosyncratic risk they face – that is, to hedge – but they can only do so imperfectly because markets are incomplete and the contract that traders have access to is not perfectly negatively correlated with their endowment risk. The pay-offs on a contract are symmetric around zero – traders are equally likely to owe money on a contract as they are to receive it. The OTC derivatives contract is the only way traders can manage endowment risk. This assumption is designed to capture the specific nature of financial risks that we have in mind when financial market participants engage in OTC market trade. It is different from other incomplete markets models, such as Bewley models, where traders can self-insure (for example, through savings) against endowment risk. The structure of our model is designed to be akin to the trades between banks and other large financial firms, but abstracts from the actual source of the risk – that is, we do not model the dealer-client structure explicitly.
Traders also face counterparty credit risk. That is, when extreme price movements occur one of the parties to the trade is assumed to default and no contract payment is made. In such a state, the marginal utility of the holder of the hedge (who is expecting, but not receiving, payment) is likely to be high, because of the low payout on the underlying asset they are trying to hedge. This makes default costly. The only way traders can mitigate counterparty credit risk in our model is to novate contracts with the CCP. We do not consider other ways of managing bilateral counterparty credit risk, such as bilateral margin or CDS. To the extent that these alternative mechanisms are used, they might reduce the value of insurance provided through a CCP. However, both bilateral margin and CDS provide only partial insurance and, thus, even in these cases it is likely that the insurance benefits from central clearing will exist.[9]
The advantages of using a consumption-based asset pricing model are threefold. First, it allows for optimising behaviour on the part of traders, so that traders can endogenously respond to changes in the regulation of OTC derivatives markets. This is an important benefit relative to much of the existing literature on OTC derivatives markets because market participants' behaviour is unlikely to remain constant in the face of such policy changes. Second, our approach allows quantitative statements to be made about the relative efficiency of alternative policies. In the existing literature, it is often the case that one policy can be ranked qualitatively relative to other policies, but quantitative statements such as the optimal level of margin or the optimal level of mandatory clearing are much more difficult to infer. Third, our model has an appealing theoretical interpretation in terms of sharing counterparty risks, which are a fundamental reason CCPs exist.
Of course, our approach has limitations as well. In particular, we must abstract from many of the important features of OTC derivatives that the existing literature has studied. For instance: we do not consider how networks affect the structure of risk and the efficiency of netting arrangements (e.g. Duffie and Zhu 2011; Heath et al 2015); the relationship between clients and dealers (Neklyudov and Sambalaibat 2015); or the role of market information and opacity (Acharya and Bisin 2014). These are important considerations for policymakers, but are beyond the scope of our paper.
The rest of this section sets out the model formally. We first introduce our traders and the model structure without the CCP to illustrate the underlying decision problem (Sections 3.1 to 3.4). We then introduce the CCP and show how that affects traders' maximisation problems (Section 3.5). Next, we characterise the equilibrium of our model, along with an alternative ‘constrained-efficient’ benchmark (Section 3.6). Section 3.7 details how we calibrate the model.
3.1 The Markets and Contracts
There is a continuum of markets on the unit interval, indexed by m. Each market could represent a particular product: one market might represent 10-year Australian dollar-denominated fixed-for-floating interest rate swaps; another, 1-year Japanese yen-denominated overnight index swaps; and another, 3-month Australian dollar-US dollar forwards.
There are two types of traders within each market – a ‘long trader’ and a ‘short trader’. We assume a unit mass of identical long traders and, separately, short traders within each market. This implies that each trader takes the price of the contract as given. Because all long traders within a market are identical and are price takers, we use a representative long trader (and likewise for short traders).
All long traders in market m receive a market-specific endowment Am,t. All short traders in the same market m receive Ãm,t. Endowments between the two types offset exactly, such that there is no aggregate risk in a market:
where εm,t is independently and identically distributed 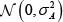 across markets.[10]
across markets.[10]
The OTC derivatives contract is an agreement to pay an amount determined by a market-specific
random variable ym,t, which is distributed 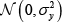 and
is negatively correlated with the stochastic component of the endowment payment,
corr(εm,t, ym,t) < 0.[11]
OTC derivatives contracts are infinitely lived, and pay out in period t + 1 based on
the volume held from period t.
and
is negatively correlated with the stochastic component of the endowment payment,
corr(εm,t, ym,t) < 0.[11]
OTC derivatives contracts are infinitely lived, and pay out in period t + 1 based on
the volume held from period t.
3.2 Default
We model counterparty credit risk by assuming that obligations on the contract are capped – that is, default is exogenous, not strategic, and depends only on the realised value of ym,t.[12] Specifically: if ym,t is negative and below a given threshold (requiring a large payment from the long trader to the short trader in market m), long traders will default and not pay what they owe to short traders. Similarly, if ym,t is sufficiently positive (i.e. above a given symmetric threshold), short traders will default on their obligations to long traders. The default thresholds are exogenous and, in the event of default, no payment is made.[13] Exogenous default is common in the literature on CCPs, although Acharya and Bisin (2014) is a notable exception.
Formally, the payments traders actually make to or receive from their counterparty are given by:[14]
This pay-off structure creates a pay-off distribution that would otherwise be normal, but where traders receive zero for any draw outside the default bounds. Figure 2 shows the density of ym,t and shades the regions where default events occur.
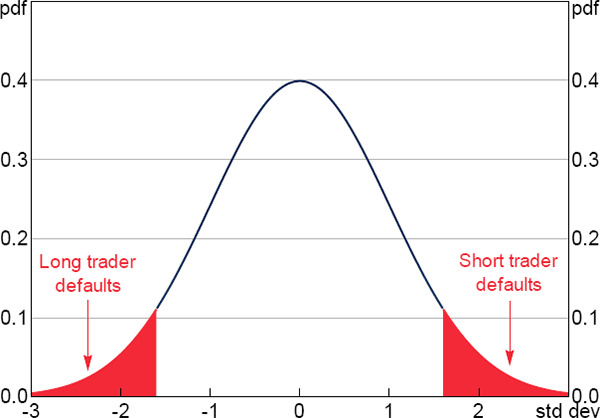
Although our representation of default is stylised, it has the advantage of being simple and highly tractable. These are important in a general equilibrium environment. We do not view our assumptions as entirely devoid of empirical content given that: traders are more likely to default when they have large obligations; the pay-off function is likely to be discontinuous; and the liability of the defaulting trader is typically limited (and the CCP's or counterparty's recovery is likely to be costly and include partial recovery at best). Notwithstanding, endogenous default would be a worthwhile extension to the extent that micro-foundations about the strategic incentive to default would more fully capture the link between wealth, price movements and the likelihood of default.
3.3 Traders' Maximisation Problems without a CCP
In the absence of a CCP, the long trader in market m maximises its lifetime utility by
choosing consumption, cm,t, and how many OTC derivatives to trade,
sm,t, in each period. We impose the usual restrictions on the utility
function: 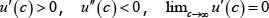 and
and 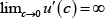 .
.
Formally, the long trader solves:
subject to the flow budget constraint:
The flow budget constraint implies that expenditure on consumption, cm,t, and purchases of OTC derivatives, pm,t sm,t, must be less than or equal to the net value of previous OTC derivatives held, pm,tsm,t − 1, the payment flow received from those OTC derivatives, fm,t sm,t, and the long trader's endowment draw for the period, Am,t.
The short trader in market m solves:
subject to the budget constraint:
3.4 First-order Conditions without a CCP
Solving the two maximisation problems presented in Section 3.3 yields two pricing equations: one for long traders and one for short traders in market m:
and:
These are similar to standard consumption-based asset pricing equations. The price in period
t – for both traders – is equal to the expected discounted value of the OTC
derivative in period t + 1 – namely, pm,t + 1 +
fm,t + 1. This pay-off is discounted by the discount rate
(β) and the stochastic discount factor 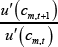 . The
stochastic discount factor measures the relative value of a unit of consumption in the next
period (for a given state) versus a unit of current consumption.
. The
stochastic discount factor measures the relative value of a unit of consumption in the next
period (for a given state) versus a unit of current consumption.
3.5 The CCP
There is one CCP that, unlike traders, has access to all markets. The CCP guarantees full payment of all obligations on OTC derivatives contracts that it clears – in effect, it provides default insurance in the event that a counterparty defaults. Because we assume a continuum of markets and that contract payouts are independent (and statistically independent of λm), a law of large numbers can be applied so that the CCP can correctly forecast its total required payout and is able to collect sufficient resources from participants to cover this payout.[15]
3.5.1 Novation
Traders in market m must centrally clear a market-specific exogenous proportion of their contracts – denoted by λm ∈[0,1]. We model central clearing by having both types of traders sell a proportion λm of their contracts to the CCP in exchange for an exactly offsetting contract with the CCP. That is, the CCP becomes the buyer to every seller and the seller to every buyer (novation). Figure 3 shows the post-novation contractual relationships between long traders, short traders and the CCP.
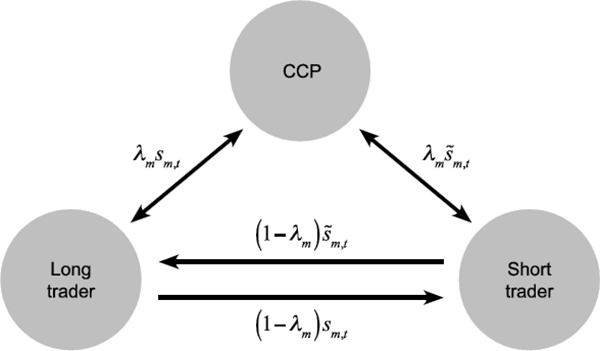
The assumption of a fixed proportion of trades with central clearing partly reflects the G20 commitment to centrally clear all standardised OTC derivatives. At face value, this implies λm = 1. However, in practice, not all derivatives are standardised enough to be centrally cleared, and not all participants are covered by mandates.[16] Nonetheless, the proportion of OTC derivatives covered by existing mandates is substantial in some markets – up to 80 per cent of new trades in the United States (CFTC 2016). In other markets, regulatory mandates are still being developed and so the proportion of trades that are centrally cleared is much lower. The modelling device of a fixed proportion of centrally cleared trades allows us to consider the full spectrum of what might eventually be able to be centrally cleared, including both boundary cases – that is, no central clearing (λm = 0), as was largely the case before the global financial crisis, and full central clearing (λm = 1).[17] Although we consider the full range of λm, we acknowledge that reality is likely to be much closer to 1 than to 0.
3.5.2 The CCP's resources
The CCP must be able to meet its obligations on OTC derivatives it clears. To do so, the CCP charges per-contract initial margin requirements (hereafter margin requirements) and collects default fund contributions from all traders.[18]
The important distinction is that margin posted, λmsm,tZ, is proportional to the number of contracts novated through the CCP, and is returned to a trader if they do not default. In the event of default, only the margin in excess of that required by the CCP to cover the loss is returned to the trader.[19] In contrast, the default fund contribution, λmDFt, does not depend on the number of contracts novated, and can be used to meet losses in cases where the margin posted is insufficient.[20]
In our model, traders do not earn a return on the margin they post. This makes margin costly. This is a realistic feature because CCPs only take high-quality assets to meet margin requirements, typically cash and government bonds. These assets have low yields, and thus posting margin carries an opportunity cost. Having collateral earn no return in our model captures this cost. In Australia, cash and government bonds comprise the majority of margin posted at ASX Clear (Futures) – a domestic derivatives CCP (Cheung, Manning and Moore 2014). These assets have comparatively low yields.
It is useful to define two indicator functions – D and 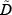 – that indicate whether the long or short trader
defaults:
– that indicate whether the long or short trader
defaults:
It is also helpful to keep track of the direction of payment flows. To this end, we define an indicator function M that denotes whether the long trader is in or out of the money:
The resources that the CCP receives in period t are given by:
There is a negative sign on the 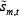 because the CCP collects
margin on both long and short positions.[21]
The gross payments the CCP makes in period t + 1 are given by:
because the CCP collects
margin on both long and short positions.[21]
The gross payments the CCP makes in period t + 1 are given by:
Although a long expression, Equation (13) is intuitive. On contracts in the money for the long trader, the CCP pays out on all contracts that the long trader has novated and collects payments from short traders, except those short traders that default. This captures the first three lines of Equation (13). The next three lines capture the measure of contracts for which the opposite happens – that is, short traders are in the money.
The CCP's budget constraint implies that the resources collected across all markets in period t must be sufficient to meet the CCP's obligations across all markets in t + 1:[22]
Using the CCP budget constraint, an appropriate law of large numbers, and Equations (12) and
(13), we can solve for the period t default fund contribution for any set of
allocations sm,t and 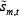 :
:
where 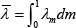 – that is, the average proportion of central
clearing across all markets.
– that is, the average proportion of central
clearing across all markets.
3.6 First-order Conditions and Equilibrium Conditions
We study two solutions to our model. The first is a decentralised solution in which traders choose their own allocations to maximise their utility taking OTC derivative prices, the proportion of OTC derivatives that must be centrally cleared, margin requirements and default fund contributions as given. The second is what we call a ‘constrained-efficient’ solution in which a planner chooses allocations on behalf of all traders in order to maximise social welfare (taking the proportion of trade that must be centrally cleared and margin requirements as given).
As we will show below, the constrained-efficient solution and the decentralised solution are not necessarily the same.[23] The constrained-efficient solution gives us a relevant benchmark for understanding how close different market structures come to the constrained optimum of the economy. Intuitively, one can think of a planner who is choosing the socially optimal level of trade and consumption, subject to the constraints that prices are market determined (markets must clear), that the planner cannot invent new contracts that better hedge risk, and cannot enforce payment in the event of default.
3.6.1 Decentralised equilibrium
The traders' problems are similar to the versions presented in Section 3.3, except that traders must now centrally clear an exogenous fraction of their OTC derivatives contracts. A long trader in market m maximises expected discounted utility by choosing consumption, cm,t, and how many OTC derivatives to trade, sm,t:
subject to the flow budget constraint:
That is, expenditure on consumption, purchases of OTC derivatives, margin requirements and the CCP default fund contribution must be less than or equal to the (net) resources received from OTC derivatives held from the previous period (including the return of margin) and the endowment.
The first-order condition is now:
Although more cluttered than the asset pricing equation without a CCP (Equation (7)), the intuition underlying the long trader's pricing equation is similar: the period t price is the expected discounted value of the contract in period t + 1. This future value comprises:
- the value of the OTC derivative in the next period: pm,t + 1
- payments from the proportion of OTC derivatives that are not centrally cleared: (1 −λm)fm,t + 1
- the net payments to or from the CCP, which depends on whether the long trader is in or out of the money: λm[M(ym,t+1)ym,t+1+(1−M(ym,t+1))fm,t+1]
- the return of margin posted, which is contingent on whether the long trader defaults or not: D(ym,t+1)max(0,Z−[fm,t+1 − ym,t+1])+(1−D(ym,t+1))Z.
Finally, margin requirements reduce the value of the contract today, because every extra contract entered into requires long traders to give up λmZ units of consumption, per contract purchased.
Similarly, the short trader in market m solves:
subject to the flow budget constraint:
where the short trader's budget constraint is slightly different: the signs on margin
requirements are reversed, because the short trader will have 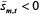 in
equilibrium and the CCP collects margin on the absolute number of contracts sold.[24]
The short trader's pricing equation is thus:
in
equilibrium and the CCP collects margin on the absolute number of contracts sold.[24]
The short trader's pricing equation is thus:
These asset pricing equations nest the non-CCP versions presented in Section 3.4 as a special case; if λm = 0, these conditions collapse to Equations (7) and (8) for the long and short trader respectively.
We now define the conditions that characterise the decentralised equilibrium. Formally, a
decentralised equilibrium is a vector of prices pm,t for each market
m and each time t, a vector of allocations 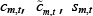 ,
and
,
and 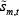 for each market m and each time t,
and a default fund contribution DFt such that:[25]
for each market m and each time t,
and a default fund contribution DFt such that:[25]
- Long and short traders' first-order conditions are met (Equations (17) and (20) respectively).
- The net supply of contracts traded in each market is zero:
- Traders' budget constraints (Equations (16) and (19)) are satisfied.
- The default fund contribution DFt satisfies the CCP's budget constraint (Equation (14)).
We further restrict our attention to time-invariant stationary equilibria, such that sm,t = sm and pm,t = pm∀t. Because the problem is recursive, the stationary equilibrium is the natural one to focus on. Moreover, doing so is consistent with the approach used for other incomplete market models, such as Bewley models.
Dropping the t subscript and denoting variables for the period ahead by primes, we solve for consumption for long traders in market m using the budget constraint (Equation (16)):
For short traders in market m:
For tractability, we assume that all markets have the same λm. This means all markets have the same solution sm. The default contribution charged by the CCP reduces to:
By combining these equations with stationary-equilibrium versions of the pricing equations, we are left with two equations (the two pricing equations) in two unknowns – sm and pm.[26] To solve the system we pick a scalar value of sm and solve for the two state-dependent price vectors pm implied by the two pricing equations (Equations (17) and (20)). This approximation implies that the quantity of contracts traded in each market is not state contingent.[27] Following Edmond and Weill (2012), we use Gauss-Hermite quadrature to approximate the pricing equations. We repeat this process for different values of sm until we find an sm such that the two pricing equations solve for the same price vector. Appendix A.2 contains further details. Because we employ a discrete approximation, many of our results have a step-like shape. We believe this is the result of the approximation, not an underlying feature of the solution. Increasing the granularity of the approximation can mitigate this problem somewhat; however, our baseline calibration with 1,225 states is already computationally expensive.
3.6.2 Constrained-efficient equilibrium
For the constrained-efficient equilibrium, a planner maximises all traders' utility
across all markets by choosing allocations 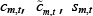 and
and 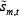 .
The maximisation problem is:
.
The maximisation problem is:
subject to the traders' budget constraints (Equations (16) and (19)), the expression for the default fund contribution (Equation (14)), and the constraint set that all markets must clear. Although the pricing equations for long and short traders are now different to the decentralised case, the approach used to numerically solve for the equilibrium is otherwise identical. Appendix B contains the Lagrangian, pricing equations and solution method for this problem. It should be noted that this benchmark is constrained-efficient in the sense that it is optimal subject to constraints of imperfect contracting (reflected in the non-unitary negative correlation between contract payouts and endowment risk), and that payment in the event of default cannot be enforced.
3.7 Calibration and Welfare
The model is calibrated to quarterly data because the majority of interest rate OTC derivatives – by far the largest and most important product in the Australian OTC derivatives market – have quarterly coupon payments. Table 1 outlines the baseline calibration.
We choose β= 0.9975 to match a 1 per cent annual rate of time preference, as in Edmond and Weill (2012); we use a constant relative risk aversion utility function, with a coefficient of risk aversion γ= 4, as is common in asset pricing literature. We choose σA to match the standard deviation of Australian aggregate household final consumption expenditure growth (0.8 per cent) to the standard deviation of trader consumption in the no-clearing version of the model. We set σy = σA without loss of generality. Traders would simply scale up or down their purchases of contracts if we changed the variance of the payout of OTC derivatives.
| Parameter | Value | Description |
|---|---|---|
| γ | 4.0 | Risk aversion |
| β | 0.9975 | Discount rate |
| σA | 0.0106 | Standard deviation in endowment payments |
| σy | 0.0106 | Standard deviation in OTC derivatives contract payments |
| corr(ym,t,Am,t) | −0.7 | Correlation between endowment and financial contract payments |
| Ā | 1.0 | Mean endowment payment |
| yupper | 2.57σy | Upper threshold, above which long traders default |
| ylower | −2.57σy | Lower threshold, below which short traders default |
| λm | 0.5 | Mandatory fraction of contracts novated through CCP |
| Z | 2.33σy | Margin required per contract |
We choose the correlation between ym,t and Am,t as −0.7 for the baseline. This implies that the OTC derivative payout will move in the same direction as the endowment payout about 25 per cent of the time, in which case the hedge will be ineffective. In the absence of detailed proprietary data it is very difficult to ascertain the average level of basis risk traders face when hedging with OTC derivatives. Accordingly, we explore a range of basis risk scenarios with correlations ranging from -1 (no basis risk/a perfect hedge) to zero (the hedge is completely ineffective).
For the mean endowment payment, Ā, we normalise this value to 1. Since default is only linked to price movements relative to the default thresholds (and is unrelated to Ā), the mean endowment payment has no effect on prices or trade allocations once we condition on the variance of consumption growth through σA, and given the assumption of constant relative risk aversion.
We set baseline margin, Z, at 2.33 standard deviations of Am,t. This level of margin coverage is consistent with the Principles for Financial Market Infrastructures (PFMI) requirement that CCPs collect margin sufficient to cover a single-tailed confidence level of at least 99 per cent of estimated future price movements (CPSS-IOSCO 2012).
For the default thresholds, we choose upper and lower bounds at ±2.57 standard deviations of Am,t, implying a quarterly rate of default of about 1 per cent (half comprising long trader defaults, half short trader defaults). Again, actual default rates are very difficult to calculate without good data. In the analysis that follows, we explore a range of default rates.
In our baseline we set λm = 0.5, implying that half of all OTC derivatives must be centrally cleared. This choice is guided by the fact that roughly half of all OTC interest rate derivatives are currently centrally cleared globally. The proportion is a bit lower in Australia – around a quarter of outstanding interest rate derivatives denominated in Australian dollars were centrally cleared as of August 2015, but more than half of outstanding interest rate derivatives denominated in G4 currencies were. A much higher proportion of new trades is centrally cleared (APRA et al 2015). In the United States – which has mandatory central clearing requirements in effect – around 80 per cent of all new interest rate derivatives are centrally cleared (CFTC 2016). We also experiment with different values for mandatory clearing in the analysis that follows.
We measure social welfare by the unconditional mean of aggregate welfare, and equally weight the utility of all traders:
In the results that follow, it is measured as the percentage lump-sum consumption transfer each period that makes traders indifferent between welfare in the relevant equilibrium we are studying (i.e. W) and a constant mean consumption stream (i.e. absent any risk).
Footnotes
Bilateral margin may not cover the full extent of the loss; CDS have counterparty credit risk associated with respect to the protection seller. [9]
We use a normal distribution, rather than a log-normal distribution (as is common in asset pricing literature), because long and short traders are on opposite sides of the distribution, and so we need a symmetric distribution. However, it does imply a very low probability of negative consumption. In practice, our calibration is such that this would be in the order of a 100 standard deviation event. Our numerical approximation ignores such unlikely events. [10]
Without loss of generality, we restrict attention to corr(εm,t, ym,t) < 0. The negative correlation implies that long traders will want to buy OTC derivatives to offset their Am,t risk; short traders will want to sell (i.e. have negative holdings) to offset their Ãm,t risk, hence our ‘long’ and ‘short’ terminology. [11]
Consistent with our incomplete markets set-up, we do not permit traders to agree on contracts that would otherwise circumvent our default mechanism. [12]
In addition, we do not assume explicit bankruptcy costs; nonetheless, as we will show, default is still welfare reducing because it reduces the effectiveness of the OTC derivatives hedge. [13]
This did not substantially change the qualitative results, although it naturally affected the quantitative results.
[14]Alternatively, if one implicitly assumes that a CCP has a small residual of its own equity, this will be sufficient to cover any deviation between the expected payout and the actual payout without affecting the CCP's viability. [15]
For instance, in Australia only internationally active dealers are covered by the current mandate. [16]
In effect, we assume that the regulatory mandate binds, and that traders would choose to clear fewer contracts in the absence of the mandate. There may be other equilibria where traders optimally choose to clear more than the regulatory mandate, but we do not focus on these because any proposed change in regulation would not affect allocations or welfare. A richer model, in which traders could choose whether to clear a contract not covered by regulatory mandates, could shed further light on whether the regulatory constraint is likely to bind in the first place. [17]
Because we calibrate our model to quarterly data, we abstract from high frequency changes in variation margin. [18]
In our model, the possibility of having more margin than loss only occurs when the margin requirement is set higher than the default threshold. We consider parameter values where this is and is not the case in our analysis. Both have occurred in recent practice: SwapClear was able to close out the Lehman Brothers portfolio in 2008 without exceeding margin; KRX had to use some of its default fund in handling the default of HanMag Securities in 2014 (although this was a futures default, not an OTC derivatives default). [19]
In reality, CCPs scale default fund requirements based on traders' activity through the CCP. However, re-sizing occurs much less frequently than initial margin is called for, and so has less immediate incentive effects. [20]
And, in equilibrium, it will be the case that 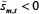 .
[21]
.
[21]
We will assume that this constraint binds in equilibrium. In effect this will imply that the CCP cannot earn positive economic profits in equilibrium (i.e. cannot extract a monopoly rent through its default contribution charge). As we note below, the CCP can exactly forecast required payouts because there is a continuum of markets. [22]
However, the constrained-efficient solution can be implemented in a decentralised equilibrium by taxing contracts on a market-by-market basis. This can be seen formally in Section 4.2.2, Equation (27). [23]
The market clearing constraint together with constant relative risk aversion utility and
the sign normalisation corr(εm,t,ym,t)<0
ensure that 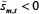 in equilibrium.
[24]
in equilibrium.
[24]
This is an abuse of notation, but reflects that we discretise the problem to solve it
numerically. More formally, prices and allocations at time t and market
m are time invariant functions: 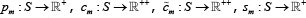 and
and 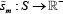 , where the state space
, where the state space 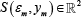 is defined for each market m ∈[0,1].
[25]
is defined for each market m ∈[0,1].
[25]
Strictly, we have infinitely many equations, because we have two equations for each market. However, all markets are identical; solving one market solves all of them. [26]
Numerically, the errors from using a non-state-contingent solution are small; see Appendix A. [27]