Research Discussion Paper – RDP 2021-09 Is the Phillips Curve Still a Curve? Evidence from the Regions
1. Introduction
As the labour market recovers from the effects of the COVID-19 shock, a key policy question facing the Reserve Bank of Australia (RBA) Board is at what point spare capacity in the labour market will be absorbed and, as a result, when will there be a sustained increase in wages growth (Lowe 2021). In other words: how strong is the relationship between unemployment and wages growth (often referred to as the wage Phillips curve), and does the nature of that relationship change as the unemployment rate falls to lower and lower levels?
Despite the importance of this question to the RBA (as an inflation-targeting central bank), the way in which aggregate wages would respond at rates of unemployment below those observed in recent history remains a key source of uncertainty, both in Australia and in other countries. In the Australian case, much of the uncertainty stems from the lack of evidence to draw upon. In the lead up to the global financial crisis (GFC), the unemployment rate declined steadily for a number of years (ultimately falling to a low of 4 per cent) and wages growth rose strongly in response. However, this was the only time over the past four decades the unemployment rate reached such a level (Figure 1).
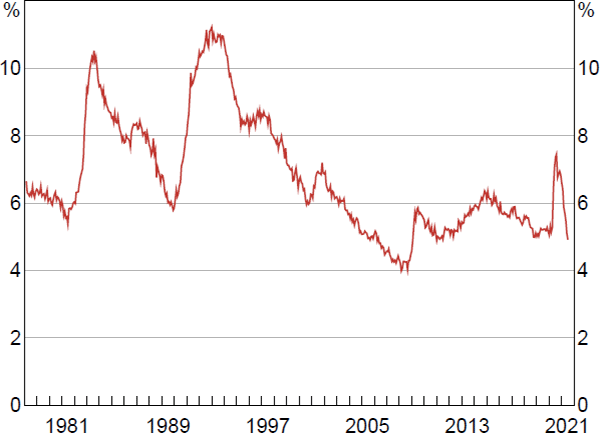
Source: ABS
This paper attempts to overcome this lack of historical experience by examining the relationship between the unemployment rate and wages growth across 291 local labour markets in Australia over the past two decades. In contrast to the national data, a panel of local labour markets provides many more observations on what happens to wages growth when the unemployment rate falls to very low levels. For example, in our dataset, more than one-fifth of all region–year observations have an unemployment rate below 4 per cent.
In examining whether the wage Phillips curve relationship is stronger at lower levels of unemployment, we contribute to a well-established literature on nonlinearities in the Phillips curve. Economists have long believed the Phillips curve to be a curve, rather than a straight line. Indeed, Phillips's (1958) original paper, as well as many introductory textbooks, show the relationship with a steeper slope when the unemployment rate is low and a flatter slope when the unemployment rate is high. This nonlinearity in the inflation–unemployment trade-off has been explicitly incorporated into the RBA's wage and price inflation models since the late 1990s, following a research discussion paper by Debelle and Vickery (1997).[1]
The question of whether the Phillips curve is a curve rather than a straight line in Australia has not been thoroughly revisited since Debelle and Vickery (1997). We believe that the time has come to re-examine the shape of the Phillips curve and test whether the functional form that underpins the RBA's current suite of Phillips curve models remains suitable. This is particularly important in light of the remarkably strong recovery in the labour market over the past 12 months and the RBA's baseline forecast for an unemployment rate approaching 4 per cent by end 2023 (RBA 2021b).
Using regional data also allows us to overcome the biases that can arise in identifying the slope of the Phillips curve using national data. These biases can arise from the endogenous response of monetary policy to economic conditions or changes in long-run inflation expectations, both of which can hinder identification of the Phillips curve in national time series data. The literature covering the US Phillips curve has demonstrated that it is important to account for these biases, and often exploits regional data to do so (Fitzgerald et al 2020; Hazell et al 2020; McLeay and Tenreyro 2020). Although the recent literature largely deals with the price Phillips curve, the same intuition applies when estimating the wage Phillips curve, which is our focus. A key advantage of using regional data to estimate the Phillips curve is that demand-driven variations in unemployment and wages that are specific to particular regions should be free from the biases that can plague estimates of the Phillips curve. However, using regional data to estimate the Phillips curve does present some challenges, most notably the task of translating regional estimates into aggregate ones.
As a benchmark, we first estimate a linear wage Phillips curve using data from 291 local labour markets over a 20-year period. Our estimates are broadly consistent with previous linear estimates for Australia and elsewhere; when the unemployment rate falls by 1 percentage point, annual wages growth increases by 0.2–0.3 percentage points on average. We then allow the slope of the Phillips curve to vary with the unemployment rate by allowing it to have a series of kinks. We strongly reject the hypothesis that the Phillips curve is a straight line – it is a curve. When the unemployment rate exceeds 7½ per cent, we cannot reject the hypothesis that the Phillips curve is flat. However, we find that the slope of the Phillips curve steepens when the unemployment rate falls below 5½ per cent, and steepens further when the unemployment rate falls below 4 per cent. Importantly, our estimates are stable over time; we find no evidence that the slope or curvature of the wage Phillips curve has changed since 2012 despite the slowdown in wages growth that has occurred since then.
Our estimates of the slope and curvature of the Phillips curve are remarkably similar to those inherent in the RBA's aggregate wage Phillips curve model, suggesting that the nonlinearity assumptions adopted following Debelle and Vickery (1997) remain broadly appropriate. The only meaningful difference emerges at unemployment rates below 3½ per cent, where the RBA's aggregate model assumes a much sharper increase in wages growth and inflation than our estimates based on regional variation.
These findings have important implications for policy. According to the RBA Board (RBA 2021a), the cash rate will not be raised until inflation is sustainably within the 2 to 3 per cent target range. The relationship between unemployment, wages growth and inflation is important for understanding how inflation will evolve. While endogenous policy makes it difficult to extrapolate from regional evidence to draw conclusions about outcomes at the aggregate level, our paper provides evidence as to the underlying relationship between unemployment and wages growth. This relationship is a key component of the broader equilibrium between unemployment, wages growth and inflation, and understanding it is crucial given the RBA's policy objectives.[2]
2. Background on the Phillips Curve and the RBA's Modelling Approach
2.1 The Phillips curve
The intuition underlying the Phillips curve is that ‘[w]hen the demand for labour is high and there are very few unemployed we should expect employers to bid wages rates up quite rapidly’ (Phillips 1958, p 283), and firms to raise prices.
Although much of the Phillips curve literature relates to the relationship between price inflation and unemployment, similar intuition applies to the wages growth–unemployment relationship. Notably, both the RBA and Australian Treasury use versions of a Phillips curve as their preferred models for forecasting nominal wages growth. In this and the following section we largely deal with wage and price Phillips curves interchangeably. However, from Section 4 on we limit our empirical analysis to the wage Phillips curve, which is the relationship we are most interested in.[3]
Since Phillips (1958), a vast amount of theoretical work has built on and formalised this basic intuition. Milton Friedman's (1968) expectations-augmented Phillips curve is:
where is inflation, is expected inflation, ut is unemployment, is the non-accelerating inflation rate of unemployment (NAIRU), and et is an error term.[4],[5] The difference between ut and is the ‘unemployment gap’. This basic framework was also extended to include supply shocks by Gordon (1982). Because neither expected inflation nor the NAIRU can be directly measured, they need to be estimated.[6]
An equation like the expectations-augmented Phillips curve also appears in many New Keynesian DSGE models, and is called the New Keynesian Phillips curve. In these macroeconomic models with sticky prices, there is a positive relationship between the rate of inflation and the level of demand, and therefore a negative relationship between the rate of inflation and the rate of unemployment.
2.2 Sources of nonlinearity
The Phillips curve above (Equation (1)) assumes the relationship between the unemployment gap and inflation is linear: a 1 percentage point increase in the unemployment gap has the same effect on inflation when the labour market is tight as it does when the labour market has plenty of spare capacity. However, Phillips (1958) himself argued that the relationship between unemployment and wages growth is likely ‘highly non-linear’ as ‘workers are reluctant to offer their services at less than the prevailing rates when the demand for labour is low and unemployment is high so that wage rates fall only very slowly’. This explanation relates to the notion of downward nominal wage rigidity - that firms are either unwilling or unable cut nominal wages. During recessions these rigidities become more binding and labour market adjustment disproportionately occurs via higher unemployment rather than via lower wages. During expansions, where rigidities bind less, more of the adjustment can occur via wages.[7] This is an important argument for a nonlinear (convex) Phillips curve, especially in a low inflation environment.
Evidence from job-level microdata up until 2018 suggests that downward nominal wage rigidity is a binding constraint for Australian employers. A histogram of job-level annual wages growth outcomes from the wage price index (WPI) shows clear evidence of a scarcity of wage cuts and an abundance of wage freezes, consistent with downward nominal wage rigidity (Figure 2). In fact, only 1 per cent of all jobs experience a wage cut in any given year, compared with around 22 per cent experiencing a wage freeze.[8]
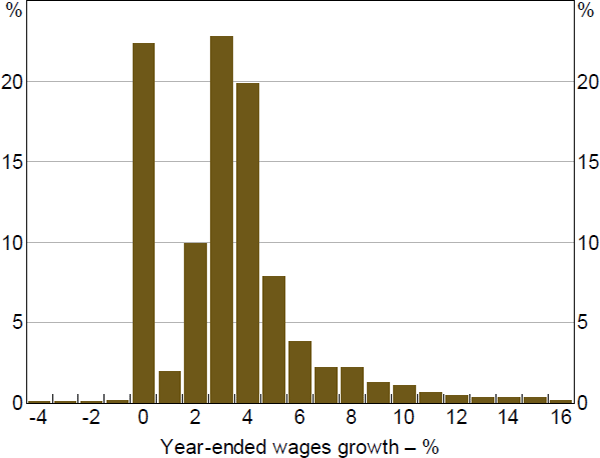
Sources: ABS (job-level wage price index microdata); Authors' calculations
Another common explanation for a convex Phillips curve is the presence of capacity constraints. This argument supposes that firms find it difficult to increase their production capacity in the short run. So, when an economy experiences a strong rise in demand, more firms will run up against capacity constraints which will push up wages and prices. Further, inflation becomes increasingly sensitive to demand; each additional increase in demand leads to ever-increasing rises in inflation. Debelle and Laxton (1997), Debelle and Vickery (1997) and Kumar and Orrenius (2016) suggest that these ‘bottlenecks’ arise when the unemployment rate falls below the NAIRU or natural rate of unemployment.[9]
Other explanations for a convex Phillips curve include menu costs and relative prices (Ball and Mankiw 1994) and efficiency wages (Shapiro and Stiglitz 1984); see Dupasquier and Ricketts (1998) for a summary of these arguments. Standard models of the labour market also imply such nonlinearity (Petrosky-Nadeau and Zhang 2017).[10]
2.3 The RBA's modelling approach
This nonlinearity in the inflation–unemployment trade-off was explicitly incorporated into the RBA's wage and price inflation models in the late 1990s, following a research discussion paper by Debelle and Vickery (1997). Prior to that, the RBA's Phillips curves were estimated in a linear framework; that is, assuming that the effect on inflation of each percentage point change in unemployment is the same regardless of the level of unemployment.
From an empirical standpoint, Debelle and Laxton (1997) and Debelle and Vickery (1997) argued that a nonlinear relationship between inflation and the unemployment gap provided a better fit to the national time series data for the United Kingdom, the United States, Canada and Australia. The equation they estimated essentially replaced the linear unemployment gap in Equation (1), , with the unemployment gap relative to the level of unemployment:
This specification implies a short-run slope equal to:
In this specification, a change in the unemployment rate has a different effect on inflation depending on both the current level of the unemployment rate and the NAIRU. Since Debelle and Vickery (1997), the RBA's workhorse wage and price Phillips curve models for policy analysis and forecasting have assumed this nonlinear relationship between inflation and the unemployment gap (Cassidy et al 2019; Ballantyne et al 2019).[11] In practice, the RBA's current models also control for other determinants of wage and price inflation, including lagged inflation and controls for supply shocks. In this paper, our discussion of the RBA's aggregate Phillips curve models focuses on the set of single-equation Phillips curve models used in constructing the RBA's central forecasts for wage and price inflation. The specifications of these models are set out in Appendix A (for wage inflation) and Cassidy et al (2019) (for price inflation). In practice, the RBA also maintains a full-system economic model for risk and scenario analysis, which adopts a similar nonlinear unemployment gap in its wages equation (Ballantyne et al 2019). Recent analysis, including the forecast scenarios for price inflation presented in RBA (2021b), has also incorporated a nonlinear unemployment gap in the inflation equation.
The functional form used in the RBA's current forecasting models for wages growth and underlying price inflation implies a high degree of nonlinearity in the Phillips curve (Figure 3). The estimates of from the RBA's model of price inflation are –2.74 and –1.90 for wage inflation. If we substitute these estimates into the expression for the slope of the Phillips curve, along with the current level of the unemployment rate (ut = 4.6 per cent) and an assumption for the NAIRU ( = 4.5 per cent), it implies that the slope of the price Phillips curve (at tangency) is –0.58, that is, a 1 percentage point change in the unemployment rate from its current level would lead to a 0.51 percentage points change in inflation. For wages growth, the slope is slightly flatter at –0.40. If we instead assumed Australia had an unemployment rate of 4 per cent, as currently forecast for the end of 2023, the RBA's preferred models imply that the Phillips curve would be 30 per cent steeper (holding and fixed).[12]
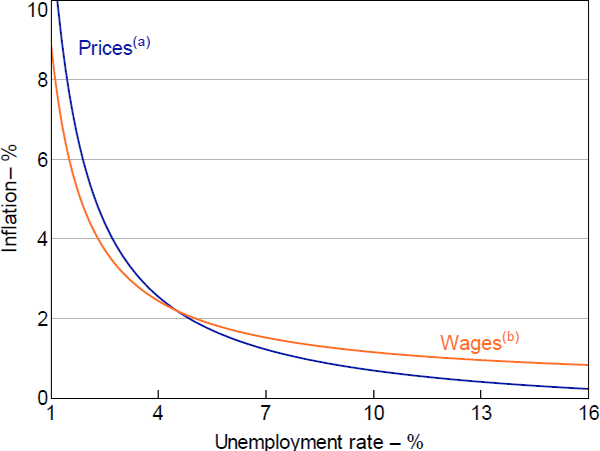
Notes:
Short run; annualised; assumes NAIRU at 4.5 per cent; the vertical position of the curves is set by assuming that when the unemployment rate equals 4.5 per cent, both wage and price inflation equal 2.2 per cent
(a) Trimmed mean consumer price index inflation; estimated over 1993:Q2–2019:Q4
(b) Private sector wage price index inflation; estimated over 1998:Q1–2019:Q4
Sources: ABS; Authors' calculations; RBA
As a consequence of this nonlinearity, the RBA's models imply that the responsiveness of wage and price inflation to a percentage point change in the unemployment rate has changed over time as the economy has moved along the Phillips curve (Figure 4).[13] Based on the estimated wage Phillips curve coefficients, inflation was increasingly responsive to changes in unemployment during the 1990s and during the resources boom, as the unemployment gap steadily declined and the economy moved to a steeper part of the curve. This gradual tightening in the labour market meant that by 2008, the economy was at a point on the wage Phillips curve that was seven times as steep as it was in the aftermath of the early 1990s recession. This trajectory reversed with the GFC, as the rise in spare capacity moved Australia to a much flatter segment of the Phillips curve.
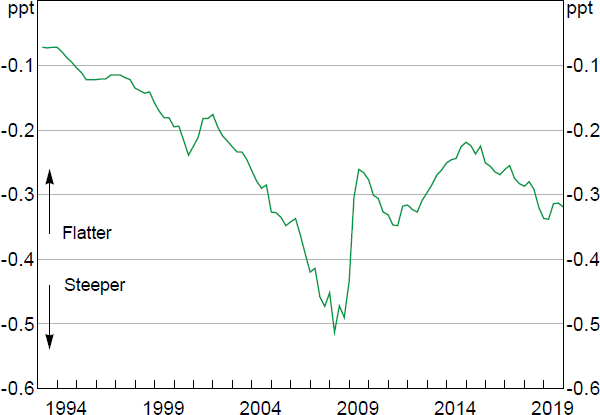
Notes: Short run; annualised; as implied by the RBA's wage Phillips curve model; assumes the NAIRU is fixed at 4.5 per cent
Sources: ABS; Authors' calculations
3. Is the Phillips Curve Still a Curve?
The question of whether the Australian Phillips curve is a curve rather than a straight line has not been properly revisited since Debelle and Vickery (1997). While Debelle and Vickery's models were originally run over a largely pre-inflation-targeting sample (1959–97), the RBA's current models use a post-1993 sample (or post-1998 in the case of wages growth due to the shorter history for the WPI). It is uncertain whether the nonlinearities that Debelle and Vickery explored for the earlier period still exist under the inflation-targeting regime. Moreover, as Debelle and Vickery (1997) noted, their results ‘should only be regarded as indicative of the presence of non-linearities’ because the aim of their paper was ‘not to estimate a definitive model’ of the Phillips curve. In light of this, it is important to examine whether the RBA's modelling assumptions remain appropriate.
There are several candidate approaches for examining nonlinearities in the Phillips curve. One approach would be to update Debelle and Vickery's time series analysis using more recent data. This would involve running a series of horse races between a linear model (e.g. Equation (1)) and nonlinear ones (e.g. Equation (2)) to gauge which perform best.[14] However, the time series data since the 1990s have few episodes of the unemployment rate going well below 5 per cent (the only case being the 2006–07 period; Figure 1). The lack of observations on tight labour markets echoes a broader challenge facing time series studies: those that try to estimate nonlinearities in the Phillips curve using national-level time series data usually find that variation in national data on unemployment and inflation is too limited to yield robust and statistically significant evidence of nonlinearity (Hooper, Mishkin and Sufi 2019).
Given the limitations of aggregate data for examining nonlinearities in the Phillips curve, a number of recent studies for the United States use state-level data instead (e.g. Kumar and Orrenius 2016; Babb and Detmeister 2017; Hooper et al 2019). These studies exploit the fact that some US states experience very tight labour market conditions even when aggregate US unemployment is elevated, and vice versa. States with unusually tight labour markets shed light on the slope of the Phillips curve when unemployment is very low. Similarly, states with high levels of unemployment shed light on the Phillips curve slope when there is spare capacity. These studies tend to find strong evidence of nonlinearity in US data. Levy (2019) finds similar results for the euro area.
In a similar vein, we explore nonlinearities in the Australian Phillips curve using data on wages growth and unemployment rates across local labour markets. This contrasts with most previous investigations of the Phillips curve in Australia, which use national time series data (e.g. Debelle and Vickery 1997; Gruen, Pagan and Thompson 1999; Lim, Dixon and Tsiaplias 2009; Norman and Richards 2010; Bullen et al 2014; Gillitzer and Simon 2015; Chua and Robinson 2018; Ruberl et al 2021). We focus on the wage Phillips curve rather than the price Phillips curve. Our data cover 291 local labour markets at annual frequency over a 20-year period. We focus on small regions, rather than states as in the US literature, because Australia has few states and labour market conditions often vary substantially within each state. This sub-state variation provides us with additional useful information for estimating how the slope of the Phillips curve varies with the level of labour market slack.
3.1 Identification of the Phillips curve
Another important development in the literature in recent years is the increasing awareness of the identification problems affecting estimates of the slope of the aggregate Phillips curve. There is a growing recognition that estimating the parameters of Equation (2) using OLS will yield biased estimates of the ‘true’ Phillips curve parameters. By ‘true’ Phillips curve, we mean the underlying structural (or causal) relationship between unemployment and inflation in the economy.
In particular, Phillips curve identification can be complicated due to three main endogeneity issues:
- the systematic response of monetary policy to economic conditions
- imperfect controls for inflation expectations
- measurement error in the unemployment gap.
Regional variation provides a way of dealing with these endogeneity issues and thus obtaining an unbiased estimate of the Phillips curve slope. This provides a second motivation for our use of regional data, in addition to the greater power it provides for detecting nonlinearities. While these issues are usually framed in the context of linear New Keynesian Phillips curve models (microfounded formulations of the Phillips curve based on rational expectations and staggered price and wage setting), the same intuition applies to nonlinear Phillips curves. In what follows, we seek only to convey the broad intuition for each issue and how it is addressed using regional data.
3.1.1 The systematic response of monetary policy
The first issue is the bias that can be introduced into Phillips curve estimates by the endogenous response of monetary policy to economic conditions. This issue is discussed in several recent papers (Fitzgerald et al 2020; McLeay and Tenreyro 2020; Hazell et al 2020), all of which were motivated by the observation that the US Phillips curve appears to have ‘flattened’ in recent decades. These papers argue that the true Phillips curve has not flattened to the extent that a simple regression of aggregate inflation on the aggregate unemployment gap would suggest. Rather, they argue that the observed inflation and unemployment data have been affected by changes in the conduct of monetary policy in a way that simply makes it appear as though the Phillips curve has become flatter. Specifically, several studies have argued that this bias is large enough to account for all of the apparent flattening of the US Phillips curve over time, and that the true Phillips curve is steeper and more stable than time series data suggest (Fitzgerald et al 2020; McLeay and Tenreyro 2020).[15]
The intuition provided by McLeay and Tenreyro (2020) is as follows.[16] A central bank with a dual mandate for achieving full employment and inflation at some target level will respond to the various shocks that hit the economy by weighing up these two objectives. Optimal stabilisation policy tries to fully offset the effects of demand shocks, because these shocks do not create a trade-off between the central bank's objectives. For example, a negative demand shock that causes inflation to fall below target and unemployment to rise above target can be addressed by expansionary policy which will help to return both variables to the desired levels. If the central bank succeeds in offsetting the effects of demand shocks, most of the remaining variation in the data for inflation and unemployment will reflect the effects of cost-push shocks.[17] Cost-push shocks move the economy away from the central bank's inflation target without necessarily moving the economy away from full employment. Because cost-push shocks induce a trade-off between the central bank's objectives, optimal policy does not attempt to fully offset them.
A central bank's response to demand shocks will make it harder to find evidence of a Phillips curve in the data, because demand-driven variations are precisely what we need to trace out the slope of the true Phillips curve (demand shocks lead to movements along a Phillips curve, while cost-push shocks lead to deviations from the Phillips curve). The central bank's reaction to cost-push shocks exacerbates this identification issue. Cost-push shocks move inflation independently of demand, and optimal policy may involve leaning against these shocks rather than ‘looking through’ them. For example, in response to a persistent negative supply shock a central bank may tighten policy to prevent inflation straying too far from target (tolerating a higher unemployment rate to achieve this).[18] In this case, the data may show a positive correlation between inflation and unemployment. If the variation used to estimate the slope of the Phillips curve is contaminated like this, a simple regression of inflation on the unemployment gap will yield a slope estimate that is biased, and could even have the ‘wrong’ sign. The extent of the bias will depend on the extent of the cost-push shocks (and whether policy responded), relative to any residual variations in demand that policy was not able to offset.
One solution to this endogeneity problem is to include controls for cost-push shocks (and other trade-off-inducing shocks) in the model. The price Phillips curve model used by the RBA controls for import prices, and also uses a measure of inflation (trimmed mean) that filters out the effects of large cost-push shocks. As such, the RBA's preferred models control for at least some of the potential bias due to endogenous monetary policy. However, there are many trade-off-inducing shocks that monetary policy could respond to that are not controlled for (e.g. changes in trend labour productivity and financial frictions), so it is possible that the model estimates are still affected by endogenous policy.
Using regional variation as we do in this paper is another solution to the identification problem. Because monetary policy only responds to aggregate shocks, region-specific variation can be used to identify the true causal relationship between inflation and unemployment (Fitzgerald et al 2020; McLeay and Tenreyro 2020). Since monetary policy does not offset region-specific demand shocks, region-level data can provide us with the variation we need to trace out the slope of the Phillips curve even when policy is fully stabilising demand at the national level. Moreover, including time fixed effects in a regional panel model will account for the endogenous response of monetary policy to aggregate trade-off-inducing shocks that would otherwise bias our estimates of the Phillips curve.[19]
3.1.2 Inflation expectations
Another issue facing national time series estimates of the Phillips curve is that direct measures of long-term inflation expectations are often poorly measured or not available. This can bias estimates of the slope of the Phillips curve if movements in long-run inflation expectations are correlated with changes in the unemployment rate. Hazell et al (2020) point to the disinflation in the United States in the early 1980s as an important example of this. The authors argue that the willingness of the Federal Reserve under Chairman Volcker to allow unemployment to rise to a high level sent a credible signal to the public about its commitment to reducing inflation. In turn, this caused a decline in long-run inflation expectations which contributed to the fall in inflation. Because long-run inflation expectations and inflation were declining at the same time that unemployment was rising, failing to control for the former in a Phillips curve model would lead one to overestimate the steepness of the Phillips curve.
Studies focusing on the flattening of the Phillips curve after the 1980s clearly need to address this issue. However, this is less of a concern for the RBA's current estimates of the Phillips curve. First, the RBA's existing suite of Phillips curve models control for long-term inflation expectations directly, which minimises the bias discussed by Hazell et al (2020).[20] Second, the estimation samples for the RBA models span a stable monetary policy regime.[21] Inflation targeting substantially reduced the variability of expectations, anchoring them at the RBA's target of 2 to 3 per cent. If true long-run inflation expectations did not vary much over the inflation-targeting period, any confounding effect of shifting long-run expectations would be small even if the measure used to proxy those expectations is not perfect.
Regional data provide a stronger approach to controlling for shifts in long-run inflation expectations (Hazell et al 2020). While short-run inflation expectations can differ across Australian regions due to differences in local economic conditions, long-run inflation expectations should evolve uniformly across regions to the extent they are determined solely by the credibility of the RBA's inflation target (which is common to all regions). When estimating the Phillips curve using a panel of regions, all changes in long-run inflation expectations will be absorbed by time fixed effects.[22] Hazell et al (2020) argue that this ability of regional models to control for long-run expectations partially explains why estimates of the slope of the US Phillips curve for the pre-1990s period are much ‘flatter’ using regional data than using aggregate data. Notwithstanding this, given that the RBA's existing models are estimated over a period with stable long-run inflation expectations, we do not expect that they are significantly affected by this issue and, as such, we do not expect this to lead to our regional estimates being significantly different to existing aggregate estimates.
3.1.3 Measurement error in the unemployment gap
Like inflation expectations, another variable we cannot directly observe is the NAIRU. There is evidence that the NAIRU has fallen over the past 20 years or so, in line with the general decline in the unemployment rate over the same period (Cusbert 2017; Cassidy et al 2019). In saying that, there are various reasons to be cautious about estimates of the NAIRU, including their wide confidence intervals and sensitivity to model specification and estimation window.[23] Any measurement error in the NAIRU will bias the estimated slope of the Phillips curve towards zero (Ball and Mazumder 2011).[24]
Again, regional data can provide a partial solution. Using regional data, it is possible to adopt a specification which uses the unemployment rate instead of the unemployment gap and relies on time fixed effects to sweep out any movements in the aggregate NAIRU over time. Region-specific time trends can also be included in the model to account for the possibility that the NAIRU has a different time trend across different regions.
4. Data
4.1 Local labour markets
We assume that Australia can be carved up into a number of distinct local labour markets. Theory tends to define local labour markets as geographic areas with similar wages, unemployment rates and housing costs, along with strong commuting links within the area (Moretti 2011). The challenge is to translate this notion into classifications suitable for empirical analysis. As mentioned earlier, one option would be to use states to represent local labour markets as is often done in the US literature. However, as there are only eight states and territories in Australia this would leave us with little cross-regional variation.
Another option would be to use the ABS ‘Statistical Area’ classifications to represent local labour markets. However, these classifications have a number of drawbacks. Namely, ‘Statistical Area Level 4’ regions (SA4s), although designed to represent local labour markets, have a minimum population limit (100,000 people) that can result in several distinct labour markets being grouped together, particularly outside of the major cities. At the other end of the spectrum, ‘Statistical Area Level 2’ regions (SA2s) (the smallest areas for which data on wages and unemployment are available) are so small (roughly 3,000 to 25,000 people) that people in cities are likely to live in a different SA2 to the one in which they work. This inter-regional commuting would muddy our analysis.
This suggests that an optimal classification of local labour markets is some combination of SA2s (in regional areas) and SA4s (in major cities).[25] Rather than simply classifying local labour markets based on whether they are located in major cities or regional areas, we apply a cluster analysis algorithm to data on intra-regional commuting patterns from the Census to group together SA2s with the strongest commuting ties. This approach is similar to the ‘commuting zones’ commonly used in US research dealing with local labour markets. Our approach provides more than three times the number of distinct labour markets than SA4s, without compromising on the notion that local labour markets should have a high degree of overlap between where people live and where they work. We end up with 291 local labour markets covering the entire continent. Our approach is described in Appendix B.
4.2 Unemployment and wages growth
The building blocks of our regional dataset are the many SA2s in Australia, which are the smallest areas for which data on wages and unemployment are available. We collect annual data on average wage income and unemployment rates for each of these SA2s from 1998/99 to 2017/18. We then aggregate these areas into 291 local labour markets using the classification approach outlined above.
4.2.1 Wages growth
Our measure of wages growth is derived from the ABS ‘Personal Income in Australia’ release, which provides regional data on average employee income based on the tax records of 12 million–14 million people each year. Specifically, it provides the total employee income per employee in each SA2 for each financial year from 1995/96 to 2017/18.[26] We use these data to construct wages growth in a region as the percentage change in average employee income in that region relative to the previous year.[27]
Because our measure of wages growth is sourced from administrative data covering most employees, it is accurately measured even for fine geographic areas like SA2s. Other measures of inflation such as the WPI, average earnings from the national accounts (AENA) per hour and the consumer price index (CPI) are only available at the state and territory or capital city level.
Employee income is a broad measure of labour costs that includes wages, bonuses, allowances, superannuation and redundancy payments. This contrasts with narrower measures of wages growth, such as WPI growth, which is limited to wage payments.[28] Another difference is that, unlike the WPI, our measure of average employee income is affected by changes in hours worked per employee and changes to the composition of the workforce. We discuss this issue in Section 8.2. While we refer to our measure as ‘wages growth’ for brevity, these measurement and conceptual differences should be kept in mind.
4.2.2 Unemployment rates
Our data on regional unemployment rates are from the ‘Small Area Labour Markets’ statistics published by the National Skills Commission. Being available at the SA2 level, these data provide a finer geographic disaggregation of unemployment rates than available in the Labour Force Survey (LFS) (at the SA4 level), making it relatively easy to map them across to our 291 local labour markets.
The National Skills Commission construct these data based on Newstart Allowance/JobSeeker and Youth Allowance payment data along with data on SA4-level unemployment rates from the LFS. They measure the average unemployment rate in each region over each financial year from 1998/99 onward. Although these measures make use of reliable administrative data, the administrative data are primarily used to interpolate the LFS SA4 data, so the SA2-level data will inherit some of the sampling variability of the LFS estimates. To the extent that our data on regional unemployment rates are measured with error, this would generally be expected to bias our estimates of the slope of the Phillips curve towards zero.
4.2.3 Variation in unemployment rates
As discussed earlier, a key advantage of using regional data is that it provides more observations with very tight labour markets compared to the national time series data. This can be seen in Figure 5, which shows the distribution of unemployment rates in both the national time series and our regional panel. Over the inflation-targeting period there have been only seven quarters (2007:Q2–2008:Q4) in which the national quarter-average unemployment rate was below 4½ per cent, and in no instance did it fall below 4 per cent. For this reason, the power of tests for nonlinearities would be low when using aggregate data. In contrast, there is substantial variation in unemployment rates at the local labour market level; more than one-fifth of all region–year observations have unemployment rates below 4 per cent.[29]
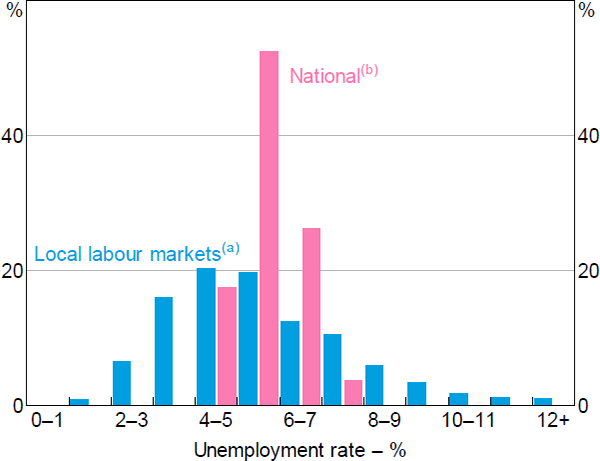
Notes:
(a) Weighted by the number of wages and salary earners in each labour market, annual
(b) Seasonally adjusted, quarterly
Sources: ABS; Authors' calculations; National Skills Commission
4.2.4 Graphical evidence
Before moving to the regression analysis, we first present a visual inspection of the wage Phillips curve relationship in our regional dataset. Figure 6 shows a binned scatter plot of unemployment rates (x-axis) against annual wages growth (y-axis) based on the 5,639 region–year observations in our data.[30] Each unemployment rate ‘bin’ is 10 basis points wide (e.g. all unemployment rates ≥5 per cent but <5.1 per cent constitute a single bin), and for each of these bins we calculate the sample average wages growth for all region–year observations within that bin.[31] The size of the markers in the figure is proportional to the number of region–year observations in the respective bin. Because the sample sizes for these narrow bins becomes very small for unemployment rates above 10 per cent, in Figure 6 we exclude all observations above that level.
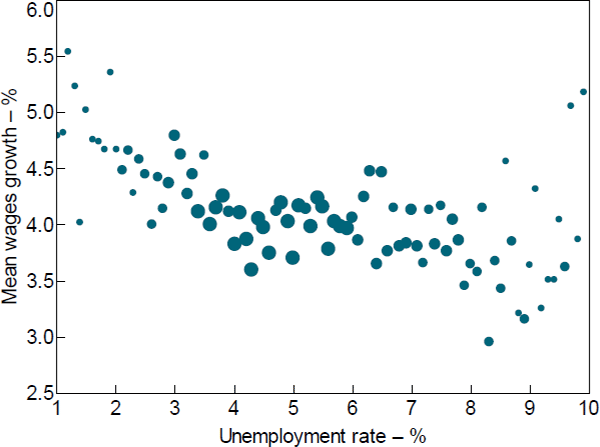
Notes: Grouped to nearest 0.1 percentage point by unemployment rate; the size of each dot is proportional to the employee-weighted number of region–year observations in each unemployment rate bin; in the figure unemployment rates are bottom-coded at 1 per cent and unemployment rates above 10 per cent are not shown
Sources: ABS; Authors' calculations; National Skills Commission
Figure 6 provides strong visual evidence of potential nonlinearity in the relationship between unemployment and wages growth in our dataset. More specifically, the data suggest a convex wage Phillips curve that is quite flat for unemployment rates above 5 per cent, but negative and steep for unemployment rates below 5 per cent, and particularly below 4 per cent. In the next section, we examine if this relationship holds when we control for a range of region-specific and aggregate-level factors.
5. Benchmark Linear Model
To provide a benchmark, we first estimate a linear wage Phillips curve that ignores the nonlinearity in Figure 6. This benchmark model also aids with comparison to the international literature, which typically uses a linear specification.
5.1 Specification
We estimate the following linear wage Phillips curve model:
where is annual wages growth in region i in year t and uit is the region's average unemployment rate during the year. The main coefficient of interest is , which is the slope of the wage Phillips curve in the short run.[32] In this model, there is no nonlinearity: the slope of the Phillips curve is the same irrespective of labour market conditions. We relax this assumption in the next section.
The model also includes lagged wages growth, which helps to control for the observed persistence in wages growth. The model includes region fixed effects to control for any permanent differences in wages growth and labour market conditions across regions. The model also has time fixed effects to capture any factors that vary across time but are constant across regions - for example, a change in federal industrial relations policy that has an equal effect on all regions. Importantly, the time fixed effects address the biases discussed in Section 3.1. Due to the well-known bias in dynamic panels and the relatively short time series dimension in our sample, we estimate the model using the Arellano-Bond procedure.
A key variable that is not explicitly included in the model is inflation expectations. Unfortunately, measures of inflation expectations are not available at the region level. However, the lagged wages growth term partially controls for region-specific inflation expectations to the extent that expectations are formed adaptively. Moreover, the region fixed effects control for permanent differences in inflation expectations across regions, while the time fixed effects control for any trends in inflation expectations that are common to all regions over time. We discuss the implications of omitting direct controls for short-term inflation expectations in Section 7.2.3.
Our model also omits an explicit control for the NAIRU. Again, the region and time effects will control for permanent differences, and common changes, in the NAIRU across regions. The main sources of omitted variable bias that could affect our results are changes in the NAIRU and inflation expectations that occur within regions over time. We can partly account for these variations by also allowing for region-specific time trends, which we do as a robustness test. To the extent that the fixed effects capture most variations in region-specific NAIRUs, the can be interpreted as capturing the effect of a 1 percentage point change in the unemployment gap.
5.2 Results
Results for the linear model are shown in Table 1. We present results from three versions of the model, all of which include region fixed effects and lagged wages growth. Column (A) shows results from a specification without time fixed effects. In this case, we find that the Phillips curve is negatively sloped; the coefficient on the unemployment rate is negative and statistically different from zero. The point estimate suggests that a 1 percentage point decline in the unemployment rate is associated with a 0.27 percentage points increase in annual wages growth.
| (A) | (B) | (C) | (D) | |
|---|---|---|---|---|
| Unemployment rate | −0.274*** (0.039) |
−0.227*** (0.045) |
−0.309*** (0.053) |
−0.220*** (0.046) |
| Lagged wages growth | 0.305*** (0.035) |
0.247*** (0.039) |
0.194*** (0.038) |
0.248*** (0.039) |
| Unemployment rate × post_2012 | −0.023 (0.031) |
|||
| Region fixed effects | Yes | Yes | Yes | Yes |
| Time fixed effects | No | Yes | Yes | Yes |
| Region-specific trends | No | No | Yes | No |
| Observations | 5,639 | 5,639 | 5,639 | 5,639 |
|
Notes: Standard errors (in parentheses) are clustered by region; ***, **, and * denote statistical significance at the 1, 5, and 10 per cent levels, respectively; estimation is done using the Arellano-Bond estimator, and weighted by the number of employees in each region Sources: ABS; Authors' calculations; National Skills Commission |
||||
In column (B) we add time fixed effects, which purge our estimates of any aggregate-level variation, including changes in monetary policy, long-run inflation expectations and the aggregate NAIRU. Surprisingly, this makes little difference to our results. If anything, the Phillips curve is estimated to be flatter (at around –0.23) when time fixed effects are included, the opposite of what we would expect if identification of the Phillips curve has been blurred by endogenous monetary policy.
The robustness of our estimates to the inclusion of time fixed effects provides tentative evidence that the endogeneity issues discussed in Section 3.1 are not relevant to Phillips curve estimation in Australia, at least for the wage Phillips curve over the post-1998 period. McLeay and Tenreyro (2020) found that the slope of the post-1990 US price Phillips curve more than doubled after adding time fixed effects to their panel model of US states. This may reflect that McLeay and Tenreyro were examining price inflation rather than wages growth, with the former being more susceptible to endogeneity than the latter.[33] It could also reflect differences in the conduct of monetary policy between the United States and Australia, or differences in the nature of the shocks that the respective central banks have faced. In any case, we proceed to use the robust version of the model – with the full set of region and time fixed effects – for the remainder of this paper.
The slope of the Phillips curve is estimated to be slightly steeper (at around –0.30) if we include region-specific linear time trends in the model (column (C)). This may suggest that region-specific NAIRUs or productivity exhibited different linear time trends over the course of our sample period.
Overall, estimates from the linear specification imply a slope of between –0.2 and –0.3, which is within the range of previously reported estimates of the slope of the wage Phillips curve. For Australia, the RBA's time series wages growth model (with a nonlinear Phillips curve specification) implies a slope of –0.29, when averaged over the 1999-2018 period. Using US state-level data, Kumar and Orrenius (2016) estimated the slope of the US wage Phillips curve to be –0.33 and Levy (2019) estimated a slope of –0.3 when using variation across regions within the euro area.[34]
Our estimates are also in line with the (more voluminous) literature on the price Phillips curve. Using data for US metropolitan statistical areas (MSAs), Fitzgerald et al (2020) estimate the slope of the price Phillips curve to be close to –0.3 across a range of specifications and sub-periods. McLeay and Tenreyro (2020), also using MSA-level data, report a preferred point estimate of –0.379. The main exception to this pattern of findings is Hazell et al (2020), who estimate a much flatter slope of the price Phillips curve at –0.006; the main reason for this is that, in their framework, they make an adjustment for the persistence of unemployment when going from their empirical specification to their estimated slope. We discuss the implications of Hazell et al's framework in Section 7.2.3 and also Appendix D.
Column (D) in Table 1 explores the stability of the estimated Phillips curve relationship over time. We examine this by interacting the unemployment rate variable in Equation (3) with a dummy variable that equals one for the period 2012-18 and zero for the pre-2012 period. A positive coefficient on the interaction term would indicate that the wage Phillips curve flattened after 2012. We choose 2012 to divide our sample because it splits our sample into the upswing and downswing phases of the resources investment boom. The extent of the slowdown in wages growth over the post-2012 period has also been somewhat of a puzzle (Harper et al 2019). We find no evidence that the slope of the Phillips curve changed between these two periods: we do not reject the hypothesis that the coefficient on the interaction term is zero (p-value = 0.451).
6. Allowing for Kinks in the Phillips Curve
6.1 A single kink
The linear specification provides a useful benchmark. However, as we will show, the assumption of linearity is strongly rejected by the data (as might be expected based on Figure 6). The simplest way of allowing the slope of the Phillips curve to vary with the level of unemployment is to use a linear spline. This lets us include a kink in the Phillips curve at some threshold unemployment rate, . To estimate a linear spline with a single kink, we only need to add a single new variable to the linear specification,
The additional term allows the slope of the Phillips curve to differ when uit is above or below the kink point, (which is specified before estimation). The slope of the curve below the kink point is given by and the slope of the curve above the kink point is given by . The Phillips curve is downward sloping and convex if and . The key decision is where to place the kink point. Guided by the visual relationship that is apparent in Figure 6, our starting point is to assume that the kink in the Phillips curve (if any) will occur at an unemployment rate of 4 per cent.
The first three columns of Table 2 show results from estimating Equation (4) with set equal to 4 per cent. The three specifications are labelled (B), (C) and (D) and are the same as specifications (B), (C) and (D) in Table 1, albeit after adding the linear spline term to the equation.
Our estimates of and in specification (B) are –0.73 and 0.56, respectively (both statistically significant at the 1 per cent level). This suggests that a 1 percentage point fall in the unemployment rate is associated with an increase in wages growth of 0.73 percentage points when the unemployment rate is below 4 per cent, and 0.17 percentage points when it is above 4 per cent. The statistically significant coefficient estimate for means that we can reject the null hypothesis that the Phillips curve is a straight line.
| Linear spline with single kink | Restricted cubic spline with three kinks | ||||||
|---|---|---|---|---|---|---|---|
| (B) | (C) | (D) | (B) | (C) | (D) | ||
| Unemployment rate | −0.734*** (0.206) |
−0.774*** (0.213) |
−0.733*** (0.215) |
−0.484*** (0.106) |
−0.515*** (0.109) |
−0.512*** (0.102) |
|
| Linear spline term | 0.561*** (0.200) |
0.512** (0.203) |
0.579*** (0.219) |
||||
| Restricted cubic spline term | 0.300*** (0.087) |
0.239*** (0.088) |
0.357*** (0.088) |
||||
| Lagged wages growth | 0.236*** (0.040) |
0.186*** (0.038) |
0.238*** (0.040) |
0.239*** (0.039) |
0.188*** (0.038) |
0.241*** (0.039) |
|
| Unemployment rate × post_2012 | −0.095 (0.265) |
0.097 (0.082) |
|||||
| Linear spline term × post_2012 | 0.048 (0.303) |
||||||
| Restricted cubic spline term × post_2012 | −0.183 (0.111) |
||||||
| Region fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | |
| Time fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | |
| Region-specific trends | No | Yes | No | No | Yes | No | |
| Observations | 5,639 | 5,639 | 5,639 | 5,639 | 5,639 | 5,639 | |
|
Notes: Standard errors (in parentheses) are clustered by region; ***, **, and * denote statistical significance at the 1, 5, and 10 per cent levels, respectively; estimation is done using the Arellano-Bond estimator, and weighted by the number of employees in each region Sources: ABS; Authors' calculations; National Skills Commission |
|||||||
Again, the estimated Phillips curve is slightly steeper – both above and below the kink point – when we allow for region-specific time trends in column (C). And once again, there is no evidence that the slope (or convexity) of the Phillips curve changed after 2012 (specification in column D). In all three specifications, we reject the null hypothesis of linearity at the 1 per cent level of significance. The estimated Phillips curve is convex to the origin, consistent with the assumption in the RBA's aggregate workhorse models following Debelle and Vickery (1997).
6.2 Allowing more curvature
A single-kinked spline may not be flexible enough to capture the curvature of the Phillips curve. To allow for more curvature, we also estimate the wage Phillips curve using a linear spline with three kinks: at unemployment rates of 4 per cent, 5.5 per cent and 7.5 per cent. The locations of these kink points are consistent with similar research for the United States (Leduc, Marti and Wilson 2019; Hooper et al 2019), and correspond to the 23rd, 53rd and 80th percentiles of the distribution of observed unemployment rates in our sample. We plot the estimated Phillips curve using this triple-kinked specification in Figure 7.[35] The estimated Phillips curve is convex to the origin, and the null hypothesis of linearity is rejected at the 1 per cent level of significance (based on a joint test of significance of all three spline terms).
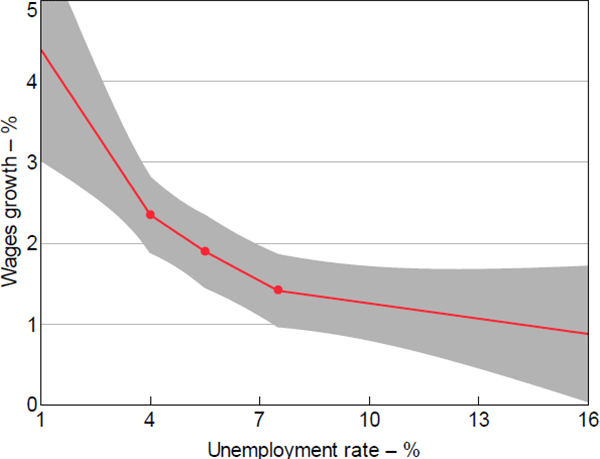
Notes: 95 per cent confidence intervals estimated using the Delta method; dots denote kinks at 4.0, 5.5 and 7.5 per cent
Sources: ABS; Authors' calculations; National Skills Commission
In Figure 7, the slope of the Phillips curve at unemployment rates below 4 per cent is –0.68 (p-value = 0.002), which is only slightly smaller than our estimates at similar levels of unemployment in the single-kink specification. The slope is flatter at –0.30 for unemployment rates between 4 per cent and 5.5 per cent, and flatter still at –0.24 for unemployment rates between 5.5 per cent and 7.5 per cent. When the unemployment rate exceeds 7.5 per cent, the Phillips curve is almost completely flat; the point estimate of –0.06 is not statistically different from zero (p-value = 0.200).
It is important not to get too hung up on the vertical position of the curve in Figure 7, as this is not something that is pinned down by our modelling framework. For example, the figure should not be read as indicating that wages growth will be 2.2 per cent at an unemployment rate of 4.5 per cent. The vertical intercept of the curve in the figure (and similar figures below) is purely illustrative and based on an assumption that wages growth will equal 2.2 per cent when the unemployment rate is 4.5 per cent. In reality, the vertical position of the curve in the wages growth–unemployment space will depend on the NAIRU, inflation expectations and trend productivity growth. While our approach controls for the confounding effects of these variables, it does not estimate them. In other words, our model tells you about the slope and curvature of the Phillips curve, but it does not tell you everything you need in order to make a wages growth forecast based on the unemployment rate. The Phillips curve will shift over time as either the NAIRU, inflation expectations or productivity growth changes.[36]
To allow for even more curvature, we adopt a restricted cubic spline specification, which was used by Kumar and Orrenius (2016) in their study of the US wage Phillips curve. This method approximates the curvature of the Phillips curve between the first and third kinks (4 per cent and 7.5 per cent respectively) using a cubic polynomial. The Phillips curve is again assumed to be linear below 4 per cent unemployment and above 7½ per cent unemployment.[37] The advantage of this approach is that it can flexibly capture any curvature in a parsimonious way (e.g. Harrell 2001, p 23; Kumar and Orrenius 2016). In fact, the approach involves adding just one additional variable (a cubic spline term) to the linear model shown in Equation (3).
The results are shown in the final three columns of Table 2. The coefficient on the cubic spline term is statistically significant at the 1 per cent level across all three specifications, which once again means that linearity is strongly rejected. Figure 8 plots the estimated Phillips curve using the restricted cubic spline (specification in column (B)), along with the 95 per cent confidence intervals. This provides further evidence that the Phillips curve is nonlinear and convex. (We have not imposed this convexity on the model, we are letting the data speak). The estimated Phillips curve is very similar to the linear spline in Figure 7. The estimates in Figure 8 are our preferred estimates of the wage Phillips curve using regional data, given the flexibility and parsimony of the model.
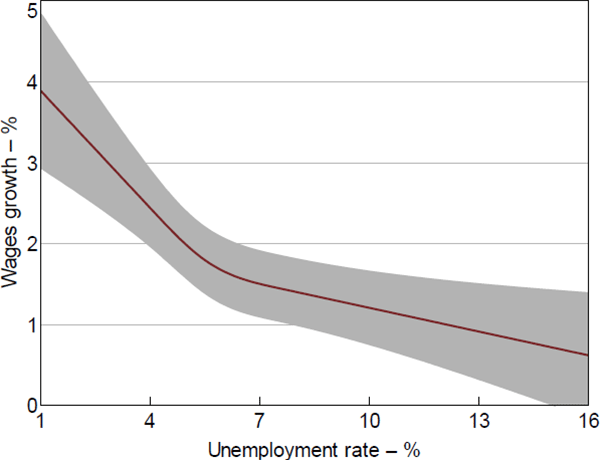
Notes: 95 per cent confidence intervals estimated using the Delta method; kinks set at 4.0, 5.5 and 7.5 per cent
Sources: ABS; Authors' calculations; National Skills Commission
7. Comparison to Aggregate Models
7.1 The RBA wage Phillips curve
One of the motivations for this paper was to test whether the functional form that underlies the RBA's Phillips curves is sensible. To examine this, Figure 9 compares our estimates of the slope and curvature of the Phillips curve using the cubic spline (regional data) to the RBA's estimates using the Debelle and Vickery (1997) functional form (aggregate data). The ‘RBA aggregate’ line in Figure 9 plots the curve implied by plugging the annualised estimated model coefficient, , from the RBA's current aggregate wage Phillips curve equation set out in Appendix A into Equation (2) for each level of unemployment.[38] The ‘Regional data’ line plots the curve implied by the results from our preferred cubic spline specification. In this figure, the vertical positions of both curves are arbitrarily pinned down based on an assumption that wages growth will equal 2.2 per cent when the unemployment rate is 4.5 per cent.
For unemployment rates above 3½ per cent, the slopes of the two curves are virtually identical. The fact that the estimates are so close is perhaps surprising, given that they are based on data at different levels of aggregation and use different sources of variation. It is only when the unemployment rate falls below 3½ per cent that a gap between the two sets of estimates opens up - in the RBA's aggregate model, wages growth starts to increase rapidly, whereas in our model the response of wages growth is more muted.
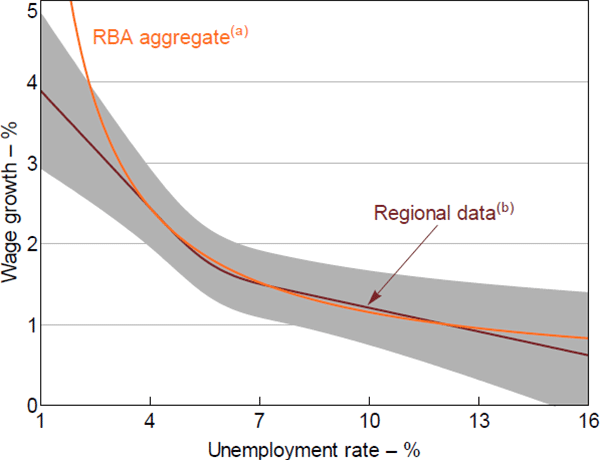
Notes:
Short run; annualised; assumes NAIRU at 4.5 per cent; the vertical position of the curves is set by assuming that when the unemployment rate equals 4.5 per cent, wage growth equals 2.2 per cent
(a) Private sector wage price index inflation; estimated over 1998:Q1–2019:Q4
(b) Restricted cubic spline; 95 per cent confidence intervals estimated using the Delta method
Sources: ABS; Authors' calculations; National Skills Commission; RBA
Overall, our results provide support for the RBA's existing modelling framework at the current juncture. The nonlinearity assumptions imposed by the RBA's wage Phillips curve model, together with the aggregate data, do a relatively good job of capturing the relationship at national unemployment rates above 3½ per cent. However, this assessment would need to be re-evaluated if the labour market were to tighten materially and the unemployment rate were to fall below 3½ per cent. If this were to happen, then our results would suggest caution in generating inflation forecasts using the highly nonlinear response of wages growth and inflation currently embodied in the Debelle and Vickery (1997) specification. While wages growth and inflation would increase, our results suggest they would not rise exponentially.[39]
Implicit in this comparison between the RBA's aggregate model and our regional model is the assumption that estimates from the latter can be reliably compared to the former. We turn to this below.
7.2 Aggregation issues
Does it make sense to infer the slope of the aggregate Phillips curve based on regional variation in wages and prices?
This question has been posed by other papers in this field. To clarify thinking around this issue, a number of these papers develop theoretical frameworks that link the parameters estimated using regional variation (in a panel model with time fixed effects) to the structural parameter that policymakers ultimately care about – the slope of the national Phillips curve. These papers take a typical single economy New Keynesian model and adapt it to the case where there are many distinct regions. In these models, each region is part of a monetary union – for example, individual states within the United States, or individual countries within the euro area. Hazell et al (2020) and Fitzgerald et al (2020) develop this type of model for the price Phillips curve, while Levy (2019) does the same for the wage Phillips curve.
These models clarify that estimates of the Phillips curve based on regional variation are informative about the slope of the ‘structural’ Phillips curve facing policymakers. Indeed, as discussed in Section 3.1, these models highlight how regional variation helps to overcome the endogeneity issues that can face an econometrician when using national time series data. However, the models also show that there are some factors we need to keep in mind when translating regional estimates into aggregate ones.
7.2.1 Nationally-set wages
One key insight from Hazell et al's (2020) model is that it is important to distinguish between tradeable and non-tradeable inflation when estimating the price Phillips curve using regional variation. By definition, non-tradeable goods and services are only consumed in the region in which they are produced, while the market for tradeable goods and services is fully integrated across regions. This means that consumers in different regions can face different prices for non-tradeables, but the same prices for tradeables. An implication is that the slope of the regional Phillips curve for overall inflation (aggregating both tradeables and non-tradeables) will understate its aggregate counterpart because the prices of tradeable goods at the regional level are insensitive to slack at the regional level. In other words, the regional CPI is less sensitive to regional unemployment than the aggregate CPI is to aggregate unemployment, because tradeable inflation is only affected by aggregate unemployment. For this reason, Hazell et al (2020) focus on non-tradeable inflation as the dependent variable in their analysis of regional data, and then use their estimates to make inferences about the slope of the Phillips curve for overall CPI at the national level.
The implications of Hazell et al's analysis are less clear when examining regional variation in wages. If labour is mobile across the tradeable and non-tradeable sectors within a region, then in theory wages should equalise within that region even if prices do not (Moretti 2011). In saying that, it could be that some wages are set at the national level and are not tailored to local economic conditions. For example, some large firms which employ workers across multiple regions of Australia can pay geographically uniform wages. The minimum wage and Australia's detailed system of award wages also apply uniformly across regions, and as such are largely set in response to conditions in the national labour market. All else being equal, this would imply that regional estimates of the wage Phillips curve underestimate the strength of the wages growth–unemployment relationship at the national level.
To explore this, we looked at whether the regional Phillips curve is flatter in regions where a larger share of wages are set at the national level, rather than locally. While we do not have a reliable measure of nationally-set wages, as a proxy we use the estimated share of employees whose wage is set according to an award, based on the region's industrial mix of employment and data on rates of award reliance by industry at the national level. We then take Equation (3) and add an interaction between this ‘award share’ variable and the local unemployment rate. The coefficient of interest is the coefficient on the interaction term, which tells us whether the Phillips curve slope is different between regions that have a larger share of their wages set according to awards, rather than local conditions, vis-à-vis regions with less award reliance. We find the coefficient on this interaction term in the linear model is positive and statistically significant, suggesting that the regional Phillips curve is flatter in regions with a larger award share.[40] However, this is a very rough proxy for the prevalence of nationally-set wages in a region, because ‘award share’ is not a direct measure of award reliance in the region and because award reliance is only one way that wages can be set nationally.
Exploring this issue in further detail using linked employee–employer data would be a fruitful area for future research. Alternatively, we could simply concede that a bias from nationally-set wages probably does exist, and apply a scaling factor to correct for it. Again, Hazell et al's (2020) theoretical model provides guidance here. It implies that the slope of the Phillips curve estimated using regional consumer prices (capturing both tradeables and non tradeables) is smaller than the slope of the aggregate Phillips curve, by a factor equal to the expenditure share on non-tradeable goods. If we carry this intuition across to the case of the wage Phillips curve, and if we think that, say, 70 per cent of all wages in Australia are set at the local rather than national level, this implies that our regional estimate needs to be scaled up by a factor of around 1.4 (= 1 / 0.7).
7.2.2 Labour mobility
Another challenge of estimating Phillips curves using regional data is that workers can migrate to different regions within Australia to improve their wages or job prospects. Standard theory suggests that a positive demand shock in a local labour market will raise local wages relative to other regions, thus encouraging workers to move in from those regions. If labour is highly mobile in this way, it could potentially complicate inferences about the aggregate Phillips curve based on regional regressions.
Theory does not provide a strong guide in this case. Leading papers that use regional variation to estimate Phillips curves generally assume that labour is immobile across regions, in both their theoretical models and empirical analyses (Hazell et al 2020; Fitzgerald et al 2020). What is clear, however, is that labour migration is an adjustment mechanism for reducing differentials in labour market conditions across regions.[41] In the absence of any rigorous theoretical guidance, we treat this adjustment mechanism as a factor that reduces the dispersion in unemployment rates across regions, but not one that influences the relationship between unemployment rates and wages growth. In other words, we assume that labour migration reduces the precision of our estimation (by reducing the extent of cross-sectional variation) but is not a key source of bias. In any case, although slow-moving forces such as migration and labour mobility are important for pinning down the precise location of the Phillips curve (via unobservables such as the NAIRU), they should be less relevant for identifying of the slope of the curve itself (which in theory relies on shorter-term business cycle variation).
7.2.3 Persistence in unemployment fluctuations
Due to data limitations, regional Phillips curve studies (including ours) generally do not control for changes in short-run inflation expectations at the region level. In contrast, most aggregate studies of the Phillips curve (particularly those in the United States) do control for short-run inflation expectations. Hazell et al (2020) argue that this difference has implications for the interpretation of regional estimates of the Phillips curve, particularly if fluctuations in unemployment are persistent.
The logic is as follows. It is widely understood that unemployment is a persistent variable. So, if a region faces an idiosyncratic demand shock that pushes its unemployment rate up, people expect it will take several years for unemployment to fall back to pre-shock levels. As a result, they expect the region's inflation rate to be lower in the short term (compared to the no-shock baseline) due to the regional Phillips curve, so they revise down their expectations for inflation in the short run. In turn, this leads to lower actual inflation as predicted by a rational expectations model of the Phillips curve. It follows that, in the absence of controls for short-term expectations, regional estimates can overstate the true slope of the Phillips curve because the observed variation in inflation will reflect not only contemporaneous unemployment, but also an additional anticipatory effect. In contrast, time series estimates that control for short-term inflation expectations will ‘partial out’ the latter effect, and, as a result, the estimated coefficient on contemporaneous unemployment should only reflect the effect of current unemployment on current inflation. Hazell et al argue that this can help account for why regional studies tend to estimate steeper Phillips curves than aggregate studies.
Hazell et al (2020) also propose an estimation approach, consistent with their theoretical framework, which provides a way to account for persistence in unemployment fluctuations in a regional regression. We explain and implement this approach in Appendix D. In brief, we find that the slope of the linear wage Phillips curve is flatter – by a factor of 2 – when we account for unemployment persistence. Following the logic of Hazell et al, this suggests that our baseline estimates of the slope of the wage Phillips curve should not necessarily be interpreted as the true slope of the New Keynesian wage Phillips curve (a structural parameter), unless we scale them down by an appropriate amount (2). Rather, our baseline estimates of the slope of the Phillips curve will capture not only the effects of current unemployment on current wages growth, but also any additional effects that come about through the influence of current unemployment rates on short-run inflation expectations.
It should be noted that, unlike much of the US literature, the RBA's Phillips curve models control for long-run inflation expectations.[42] However, like our regional specifications, they also omit an explicit control for short-run inflation expectations. As such, all else being equal, our regional approach and the aggregate RBA wage Phillips curve model should (roughly speaking) be identifying the same slope parameter. In that sense, while neither approach can be directly interpreted as the slope of the New Keynesian wage Phillips curve, it makes sense to compare our estimates with those from the RBA's aggregate wages model as we do in Section 7.1
8. Robustness
8.1 Geographic classifications
We examine if our results are robust to the way we define ‘local labour markets’. As discussed earlier, our baseline results use our preferred classification of local labour markets derived from cluster analysis on journey to work data from the 2011 Census. Appendix C demonstrates that our results are robust to the level of geographic aggregation used in the regressions. We do this by re-estimating our preferred specification using a range of different geographic classifications as the unit of observation, including local labour markets based on the 2016 Census, SA4s, states and functional economic regions. Our estimates of the slope and curvature of the Phillips curve are remarkably insensitive to using different aggregations of the data, although precision is lower in several cases.
8.2 Compositional effects
Our measure of wages growth is based on annual employee income per wage earner. This measure of wages growth is potentially affected by changes in the composition of employment. This could affect our results if these compositional effects vary with the degree of labour market slack. For example, if average hours worked per employee tend to rise when demand for labour is strong (Bishop, Gustafsson and Plumb 2016), then the increase in annual earnings growth that we observe in a tight labour market may simply reflect people working more hours on average, not increases in hourly wages. That is, it may put an upward bias (in absolute value) into our estimates.
Unfortunately, measures of compositionally adjusted hourly wages growth are not available at the region level. The best available measure of ‘pure’ wages growth in Australia is the WPI, which tracks the hourly wages of a fixed basket of jobs over time and thus controls for changes in hours worked and changes in the composition of the workforce. The WPI (excluding bonuses) is available at the state and territory level from 1997 onward, but not at the sub-state level.[43]
To explore the extent of compositional bias in our estimates, we compare our state-level estimates using growth in average employee income per worker (Appendix C) to state-level estimates that replace the dependent variable with growth in the WPI. A large difference in the coefficient estimates between these two models may indicate that compositional effects are important to our results. Our estimates suggest that the Phillips curve is slightly flatter using the WPI than using average employee income (–0.20 versus –0.27).[44] This may suggest that compositional effects are biasing our estimates. However, this finding could also reflect the fact that average employee income is a broader measure of labour costs than the WPI, and that the income components excluded from the WPI – such as promotions, bonuses, travel allowances and fringe benefits – are more sensitive to slack (Leal 2019).
8.3 Speed limit effects
Our baseline specification relates wages growth to the level of the unemployment rate (the latter can be thought as the unemployment gap when fixed effects are included). In contrast, in the RBA's aggregate model, wages growth depends on both the level of the unemployment gap and the change in the unemployment rate (see Appendix A). The rate-of-change effect is commonly referred to as the ‘speed limit effect’ and is intended to capture the inflationary impact of rapid changes in demand.
We examine if our baseline results are robust to including the change in the unemployment rate as an additional regressor in Equation (3). The results of this robustness check are shown in the second column of Table 3, while the first column shows the baseline results for comparison. The coefficient on the change in unemployment term is close to zero and not statistically significant, and the coefficient on the unemployment rate is little changed relative to the baseline. This suggests that our results are robust to controlling for speed limit effects.[45] We arrive at a similar conclusion for our preferred specification using the restricted cubic spline; the findings are robust to adding controls for the change in the unemployment rate and the change in the spline term (column 4 of Table 3).
| Linear baseline | Linear speed limit | Restricted cubic spline baseline | Restricted cubic spline speed limit | |
|---|---|---|---|---|
| Unemployment rate | −0.227*** (0.045) |
−0.208*** (0.053) |
−0.484*** (0.106) |
−0.464*** (0.107) |
| Unemployment rate | 0.008 (0.033) |
0.016 (0.060) |
||
| Restricted cubic spline term | 0.300*** (0.087) |
0.305*** (0.090) |
||
| Restricted cubic spline term | −0.010 (0.066) |
|||
| Lagged wages growth | 0.247*** (0.039) |
0.243*** (0.043) |
0.239*** (0.039) |
0.237*** (0.042) |
| Region fixed effects | Yes | Yes | Yes | Yes |
| Time fixed effects | Yes | Yes | Yes | Yes |
| Region-specific trends | No | No | No | No |
| Observations | 5,639 | 5,639 | 5,352 | 5,352 |
|
Notes: Standard errors (in parentheses) are clustered by region; ***, **, and * denote statistical significance at the 1, 5, and 10 per cent levels, respectively; estimation is done using the Arellano-Bond estimator, and weighted by the number of employees in each region Sources: ABS; Authors' calculations; National Skills Commission |
||||
9. Conclusion
Understanding the nature of the Phillips curve relationship at very low rates of unemployment is of first-order importance to the RBA, particularly at the current juncture with a central forecast for the unemployment rate to fall to a four-decade low over the next few years (RBA 2021b). The lack of historical experience of very low unemployment rates means that studying local labour markets in Australia is a fruitful way of understanding the nature of the Phillips curve at low rates of unemployment. Regional data provides richer variation in inflation and unemployment rates, allowing for more accurate estimation of the slope of the Phillips curve at unemployment rates rarely seen in the aggregate data.
The main finding of this paper is that the Phillips curve is indeed a curve, rather than a straight line. This is consistent with the earlier work by Debelle and Vickery (1997) and findings in the international literature. The Phillips curve is a lot steeper when the unemployment rate is very low, and flatter when there is more spare capacity. Our estimates suggest that the wage Phillips curve is around three times steeper when the unemployment rate is below 4 per cent than it is when it is above 5½ per cent. At even higher rates of unemployment, the wage Phillips curve is almost completely horizontal.
Our estimates of the slope and convexity of the Phillips curve are remarkably close to those from the RBA's current models using the Debelle and Vickery specification. However, at very low rates of unemployment – that is, below 3½ per cent – our estimates suggest that wages growth may not accelerate to the same extent as implied by the RBA's published aggregate Phillips curve models. As such, caution should be exercised when interpreting forecasts and scenarios that reach these very low levels. Reflecting these findings, the forecast scenarios for wage and price inflation presented in RBA (2021b) were constructed using a relationship with a degree of curvature in between that implied by the Debelle and Vickery (1997) functional form and our regional estimates.
Another important finding from our analysis is that there is no evidence that estimates of the wage Phillips curve for Australia are contaminated by the types of biases that have been found to matter in the US literature. However, an important qualifier here is that we have only explored these biases for the wage Phillips curve, and only for the wage Phillips curve estimated over an inflation-targeting period. It's possible that these issues become more pertinent when using a longer historical sample or when modelling price inflation, which in theory is more affected by endogeneity. Although reliable CPI data are not available at the local labour market level, future work could extend our analysis using city-level CPI data to further examine these issues. Although city-level data provide less cross-sectional variation, they are available over a longer time period, making them more suited to analysing the impact of monetary policy regime change on the slope of the Phillips curve. Preliminary analysis using these price data yields qualitatively similar results to those described above for the wage Phillips curve and provides tentative evidence that the slope of the regional price Phillips curve has not changed significantly following the introduction of inflation targeting.
Our paper should not be the final word on these issues for Australia. In addition to studying other measures of wage and price inflation and different historical samples, future research could also turn to exploring some of issues that we have not fully resolved. Notably, how can we account for the fact that some wages are set at the national or international level in these regional approaches? And, is regional labour migration something that may influence the results and in what way? Emerging data sources, such a linked employee–employer data, could be particularly useful for this.
Another useful exercise for future work would be to translate our partial equilibrium analysis into a broader setting by taking our estimate of the slope of the wage Phillips curve and using it in a model with a monetary policy rule (or some other form of endogenous monetary policy). In that model one could then trace out more completely the relationship between unemployment, wages and inflation.
Appendix A: RBA Aggregate Wage Phillips Curve Specification, Coefficients and Implied Slope
The current RBA wage Phillips curve forecasting model is specified as[46]:
where:
| Quarterly growth in the wage price index (WPI) (hourly rates excluding bonuses); seasonally adjusted. | |
| ut | Quarter-average unemployment rate; seasonally adjusted. |
| Non-accelerating inflation rate of unemployment (NAIRU; described in Cusbert (2017)); two-sided smoothed quarterly estimate. | |
| Quarterly change in the unemployment rate; seasonally adjusted. | |
| Year-ended growth in the domestic final demand implicit price deflator. | |
| Trendt | Trend inflation expectations estimated using a Kalman filter (described in Cusbert 2017); two-sided smoothed quarterly estimate. |
| Dependent variable = WPI excluding bonuses | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Constant | −0.240 (0.243) |
|||||||||||||||||||||||||||||||
| 0.354*** (0.103) |
||||||||||||||||||||||||||||||||
| −0.476*** (0.122)(a) |
||||||||||||||||||||||||||||||||
| −0.151** (0.061) |
||||||||||||||||||||||||||||||||
| 0.097 (0.074) |
||||||||||||||||||||||||||||||||
| 1.070*** (0.404)(a) |
||||||||||||||||||||||||||||||||
| Adjusted R2 | 0.73 | |||||||||||||||||||||||||||||||
|
Notes: Standard errors in parentheses; ***, **, and * denote statistical significance at the 1, 5, and 10 per cent levels, respectively (a) The standard errors on these variables do not account for the generated regressor problem Sources: ABS; Authors' calculations |
||||||||||||||||||||||||||||||||
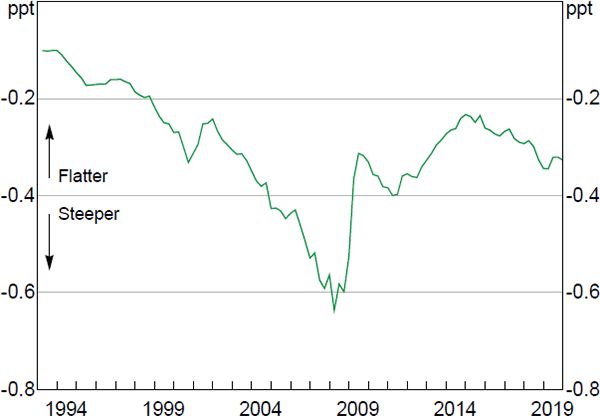
Notes: Short run; as implied by the RBA's wage Phillips curve model; uses time-varying two-sided NAIRU estimate
Sources: ABS; Authors' calculations
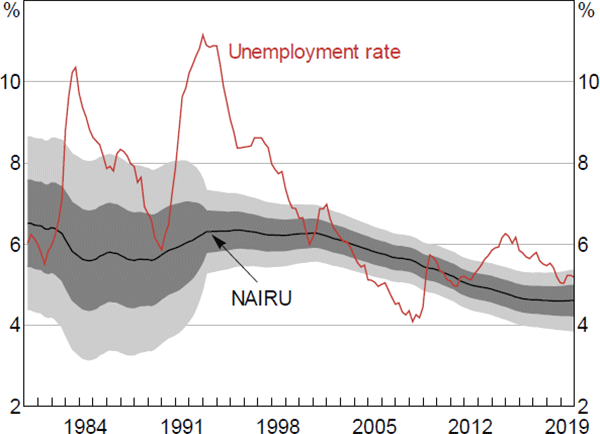
Notes: Two-sided smoothed estimates; shaded areas represent one and two standard error bands around central estimates
Sources: ABS; RBA
Appendix B: Local Labour Market Definitions
US studies often use ‘commuting zones’ to represent local labour markets across the United States (see Foote, Kutzbach and Vilhuber (2017) for a review). Commuting zones are areas with a high degree of overlap between where people live and where they work. We develop similar classifications by following the methodology used to construct US commuting zones (Tolbert and Sizer 1996), with a few modifications. Our steps are below.
Step 1: Data matrix
The building blocks of our classifications are 2,089 SA2s (at the 2011 Census), which cover the entire continent.[47]
The 2011 Census provides employment counts by ‘place of usual residence’ cross-tabulated by ‘place of work’. These cross-tabulations – in the form of a 2,089 by 2,089 matrix – provide a detailed snapshot of movements of people to and from work in 2011. Each row of the matrix represents a place of usual residence (origin), each column represents a place of work (destination), and each cell is the number of people who travel from a particular origin to a particular destination for work.
We use this data matrix to construct a 2,089 by 2,089 ‘dissimilarity matrix’. Each element Dij measures the dissimilarity of SA2 i from SA2 j :
where fij is the number of commuters who live in i and work in j, and (including fii) is the resident workforce in SA2 i .[48] Values of Dij close to zero indicate strong commuting ties between areas i and j, while values close to one indicate weak commuting ties. The main diagonal of the dissimilarity matrix is set to zero.
Step 2: Cluster analysis
The next step is to group the SA2s into a set of ‘clusters’, with each cluster representing a distinct local labour market (otherwise known as a commuting zone). To do this we perform a hierarchical cluster analysis using the dissimilarity matrix constructed in Step 1.[49] The clustering algorithm groups together SA2s based on the strength of their commuting ties.[50]
The most important decision in the procedure is at what point to stop merging clusters together. The algorithm starts out by treating each SA2 as its own cluster, and then continues to group these together – in order of how strong their commuting ties are – until we tell it to stop. If we stop the procedure too early, only the SA2s with the strongest commuting links will be merged into clusters. If we stop the procedure too late, even clusters with relatively weak commuting ties will be merged together.
The eventual number of clusters formed will depend on the ‘height’ of allowable clusters (i.e. the average between-cluster dissimilarity). As an example, at a height of 0.7 very few SA2s have been merged together – that is, most clusters will comprise a single SA2 (Figure B1). However, this changes rapidly as the height of allowable clusters is increased beyond this point: more and more SA2s are merged to form clusters and the average number of SA2s per cluster increases.
Sources: ABS; Authors' calculations
The commuting zone classifications commonly used in the United States are based on a rule that allows clusters to form that are no higher than a height of 0.98 (Tolbert and Sizer 1996). In other words, clusters that form at the 0.98 threshold are deemed to exhibit sufficiently strong commuting ties such that they should not be divided into multiple commuting zones, while clusters that form above this cut-off are deemed sufficiently distant from one another to warrant separation. This choice of cut-off value, which results in 741 commuting zones for the United States, was based on Tolbert and Sizer's (1996, p 14) observation that it ‘produced reasonable and consistent results across the wide variety of U.S. counties’.
We also define local labour markets based on a cut-off value of 0.98, to be consistent with the US research and because this cut-off value produces geographic groupings that look broadly sensible.[51]
Our local labour markets exhibit roughly the same amount of live–work overlap as SA4s (Table B1). Although higher cut-offs would increase the extent of live–work overlap, it would come at the cost of a smaller cross-sectional sample size and less integration within each labour market.
| Number of areas | Mean population (‵000s) |
Mean land area (‵000 km2) |
Mean inter-area commuting rate(a) (%) |
Mean inter-area mobility rate(b) (%) |
|
|---|---|---|---|---|---|
| SA2 | 2,196 | 10 | 4 | 65.1 | 10.2 |
| SA3 | 333 | 65 | 23 | 45.1 | 7.1 |
| SA4 | 88 | 244 | 87 | 26.9 | 4.7 |
| GCCSA | 16 | 1,344 | 480 | 4.3 | 3.5 |
| State/Territory | 9 | 2,390 | 854 | 2.5 | 3.2 |
| FERs – CofFEE | 159 | 135 | 48 | 14.7 | 5.4 |
| FERs – PC | 88 | 244 | 87 | 6.6 | 4.9 |
| Local labour markets | 291 | 74 | 26 | 29.9 | 6.8 |
|
Notes: As at 2011 Census; excludes Norfolk Island; greater capital city statistical areas (GCCSAs) include the greater capital city region of each state and the ‘rest of state’; functional economic regions (FERs) developed by the Centre of Full Employment and Equity (CofFEE) and the Productivity Commission (PC) are described in Appendix C (a) Average of the mean outbound commuting rate and the mean inbound commuting rate (b) Average of the mean annual outbound mobility rate and the mean annual inbound mobility rate (for the year to September 2011); excludes overseas arrivals and departures Sources: ABS; Authors' calculations; Centre of Full Employment and Equity; National Skills Commission; Productivity Commission |
|||||
Appendix C: Geographic Classifications and Robustness
As discussed in Section 8.1, we examine if our baseline results are robust to the way we define ‘local labour markets’. In this appendix, we discuss the results of that robustness test in more detail.
First, we examine if our results are robust to using journey to work data from the 2016 Census to define local labour markets, rather than the 2011 Census as in our baseline. This accounts for any changes in commuting patterns between 2011 and 2016 due to, say, changed transport or communications infrastructure. The estimates of the key parameters are largely unaffected by this, suggesting that changes in commuting patterns are not influencing our baseline estimates (second column of Table C1).
| Baseline | 2016 Census | SA4 | FER (CofFEE) | FER (PC) | GCCSA | State or Territory | |
|---|---|---|---|---|---|---|---|
| Unemployment rate | −0.734*** (0.206) |
−0.645*** (0.195) |
−0.804*** (0.240) |
−0.705*** (0.249) |
−0.713*** (0.253) |
−1.206*** (0.341) |
−0.883* (0.484) |
| Linear spline term | 0.561*** (0.200) |
0.490** (0.194) |
0.640*** (0.223) |
0.487** (0.243) |
0.499** (0.253) |
0.961*** (0.356) |
0.612 (0.462) |
| Lagged wages growth | 0.236*** (0.040) |
0.265*** (0.035) |
0.325*** (0.048) |
0.283*** (0.044) |
0.346*** (0.069) |
0.408*** (0.080) |
0.448*** (0.089) |
| Observations | 5,639 | 5,404 | 1,745 | 2,620 | 1,679 | 300 | 160 |
| Fraction of region-year observations with unemployment rate ≤4.0 per cent | 0.23 | 0.23 | 0.19 | 0.18 | 0.08 | 0.06 | 0.05 |
|
Notes: Standard errors (in parentheses) are clustered by region; ***, **, and * denote statistical significance at the 1, 5, and 10 per cent levels, respectively; estimation is done using the Arellano-Bond estimator, and weighted by the number of employees in each region; all models include region and time effects Sources: ABS; Authors' calculations; Centre of Full Employment and Equity; National Skills Commission; Productivity Commission |
|||||||
Our estimates are also robust to using SA4s to represent local labour markets (third column of Table C1). The main difference is in precision, with the standard errors in the SA4-level model 15–20 per cent larger than in the baseline. This may reflect that the number of cross-sectional units is more than three times larger in the latter.
Our baseline results are also robust to using ‘functional economic regions’ (FER) instead of our own approach to classifying local labour markets (fourth and fifth columns of Table C1). These alternative classifications were developed by the Centre of Full Employment and Equity (CofFEE) (Stimson et al 2016) and the Productivity Commission (2017) respectively, and are also based on the strength of commuting ties between areas.[52] While these classifications differ in a number of ways from our own, we find that using functional economic regions as the unit of analysis yields similar results to our baseline model. Again, however, estimation is less precise, which may reflect differences in sample size.
Using broad areas such as GCCSA or states and territories as the unit of analysis suggests the Phillips curve is steeper than in our baseline when the unemployment rate is both above or below 4 per cent (final two columns of Table C1). However, it is important to note that only around 5 per cent unemployment rate observations at the GCCSA or state level were below 4 per cent over our sample period. In contrast, 23 per cent of region–year unemployment rate observations were below 4 per cent using our baseline classification. Reflecting this, the null hypothesis that the Phillips curve is linear is not rejected at the 10 per cent level in the state-level model.
Overall, our estimates of the slope and curvature of the Phillips curve are remarkably insensitive to using different aggregations of the data, although precision is lower in several cases.
Appendix D: Persistence in Unemployment Fluctuations
As discussed in Section 7.2.3, Hazell et al's (2020) framework suggests that both the RBA's aggregate model and the baseline regional estimates in this paper may overstate the slope of the New Keynesian wage Phillips curve because they do not account for the persistence in unemployment fluctuations. To explore the importance of this point, we follow Hazell et al by estimating a regional panel regression that replaces the contemporaneous unemployment rate term in Equation (3) with the present discounted sum of realised unemployment rates over a five-year horizon into the future,
where the discount factor is calibrated to be 0.99. We instrument the forward sum of the unemployment rate with the first lag of the unemployment rate The forward sums in Equation (D1) mean that we lose five years of observations at the end of our sample, and the instrument means we lose one observation at the start of our sample. We estimate Equation (D1) using 2SLS.[53] We find that the lagged unemployment rate is not a weak instrument, with a first-stage F value of 59.75.
We estimate to be –0.093 (p = 0.000), which is smaller than our estimate for of –0.227 using Equation (3) (Table 1).[54] Based on the framework of Hazell et al, the larger absolute size of the slope in Equation 3 reflects the fact that the unemployment rate is standing in for the entire future sum in Equation (D1). Since unemployment is persistent, time variation in the future sum is larger than the time variation in the unemployment rate, which leads to a smaller coefficient in Equation (D1) compared to Equation (3). Note, however, that this estimation approach is based on a theoretical model of the price Phillips curve, and we have not attempted to adapt Hazell et al's theory to the context of wage inflation. In that sense, the estimates in this appendix are only suggestive of a role for persistence.
Overall, this suggests that while our regional estimates are helpful for examining the modelling assumptions in the RBA's aggregate models (as they both identify the same parameter), we should be cautious in interpreting these estimates as the structural slope of the New Keynesian wage Phillips curve.
References
Akerlof GA, WT Dickens, GL Perry, RJ Gordon and NG Mankiw (1996), ‘The Macroeconomics of Low Inflation’, Brookings Papers on Economic Activity, 1996(1), pp 1–76.
Babb NR and AK Detmeister (2017), ‘Nonlinearities in the Phillips Curve for the United States: Evidence Using Metropolitan Data’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2017-070.
Ball L and NG Mankiw (1994), ‘Asymmetric Price Adjustment and Economic Fluctuations’, The Economic Journal, 104(423), pp 247–261.
Ball LM and S Mazumder (2011), ‘Inflation Dynamics and the Great Recession’, NBER Working Paper No 17044.
Ballantyne A, T Cusbert, R Evans, R Guttman, J Hambur, A Hamilton, E Kendall, R McCririck, G Nodari and D Rees (2019), ‘MARTIN Has Its Place: A Macroeconometric Model of the Australian Economy’, RBA Research Discussion Paper No 2019-07.
Bishop J, L Gustafsson and M Plumb, ‘Jobs or Hours? Cyclical Labour Market Adjustment in Australia’, RBA Research Discussion Paper No 2016-06.
Bullen J, J Greenwell, M Kouparitsas, D Muller, J O'Leary and R Wilcox (2014), ‘Treasury's Medium-Term Economic Projection Methodology’, Treasury Working Paper 2014-02.
Cassidy N, E Rankin, M Read and C Seibold (2019), ‘Explaining Low Inflation Using Models’, RBA Bulletin, June.
Charlton A (2003), ‘Nominal Wage Rigidity in the Australian Labour Market: Evidence from Household Data’, Australian Journal of Labour Economics, 6(1), pp 25–36.
Chua CL and T Robinson (2018), ‘Why Has Australian Wages Growth Been so Low? A Phillips Curve Perspective’, Economic Record, 94(S1), pp 11–32.
Cusbert T (2017), ‘Estimating the NAIRU and the Unemployment Gap’, RBA Bulletin, June, pp 13–22.
Daly MC and B Hobijn (2013), ‘Downward Nominal Wage Rigidities Bend the Phillips Curve’, Federal Reserve Bank of San Francisco Working Paper 2013-08, January 2014.
Debelle G and D Laxton (1997), ‘Is the Phillips Curve Really a Curve? Some Evidence for Canada, the United Kingdom, and the United States, IMF Staff Papers, 44(2), pp 249–282.
Debelle G and J Vickery (1997), ‘Is the Phillips Curve a Curve? Some Evidence and Implications for Australia’, RBA Research Discussion Paper No 9706.
Debelle G and J Vickery (1998), ‘Labour Market Adjustment: Evidence on Interstate Labour Mobility’, RBA Research Discussion Paper No 9801.
Dupasquier C and N Ricketts (1998), ‘Non-Linearities in the Output-Inflation Relationship: Some Empirical Results for Canada’, Bank of Canada Working Paper 98-14.
Dupont WD (2002), Statistical Modeling for Biomedical Researchers: A Simple Introduction to the Analysis of Complex Data, Cambridge University Press, Cambridge.
Dwyer J and K Leong (2000), ‘Nominal Wage Rigidity in Australia’, RBA Research Discussion Paper No 2000-08.
Fitzgerald TJ, C Jones, M Kulish and JP Nicolini (2020), ‘Is There a Stable Relationship between Unemployment and Future Inflation?’, Federal Reserve Bank of Minneapolis Staff Report No 614.
Foote A, MJ Kutzbach and L Vilhuber (2017), ‘Recalculating ... : How Uncertainty in Local Labor Market Definitions Affects Empirical Findings’, U.S. Census Bureau, Center for Economic Studies Working Paper No CES 17-49.
Friedman M (1968), ‘The Role of Monetary Policy’, The American Economic Review, 58(1), pp 1–17.
Gillitzer C and J Simon (2015), ‘Inflation Targeting: A Victim of Its Own Success?’, RBA Research Discussion Paper No 2015-09.
Gordon RJ (1982), ‘Inflation, Flexible Exchange Rates, and the Natural Rate of Unemployment’, in MN Bailey (ed), Workers, Jobs, and Inflation, Brookings Institute, Washington DC, pp 89–152.
Gordon RJ (1997), ‘The Time-Varying NAIRU and Its Implications for Economic Policy’, Journal of Economic Perspectives, 11(1), pp 11–32.
Gruen D, A Pagan and C Thompson (1999), ‘The Phillips Curve in Australia’, RBA Research Discussion Paper No 1999-01.
Harper I, J Borland, A Charlton and S Richardson (2019), ‘Wrap-up Panel Discussion’, Discussion held at the annual Reserve Bank of Australia Conference on ‘Low Wage Growth’, Sydney, 4–5 April.
Harrell FE Jr (2001), Regression Modeling Strategies: With Applications to Linear Models, Logistic Regression, and Survival Analysis, Springer Series in Statistics, Springer, New York.
Hazell J, J Herreño, E Nakamura and J Steinsson (2020), ‘The Slope of the Phillips Curve: Evidence from U.S. States’, NBER Working Paper No 28005, rev May 2021.
Hooper P, FS Mishkin and A Sufi (2019), ‘Prospects for Inflation in a High Pressure Economy: Is the Phillips Curve Dead or Is It Just Hibernating?’, NBER Working Paper No 25792.
Kumar A and PM Orrenius (2016), ‘A Closer Look at the Phillips Curve Using State-Level Data’, Journal of Macroeconomics, 47(Part A), pp 84–102.
Leal H (2019), ‘Firm-Level Insights into Skills Shortages and Wages Growth’, RBA Bulletin, March.
Leduc S, C Marti and DJ Wilson (2019), ‘Does Ultra-Low Unemployment Spur Rapid Wage Growth?’, FRBSF Economic Letter No 2019-02.
Levy A (2019), ‘The Euro Area Phillips Curve: Identification with Regional Data’, Unpublished manuscript, Department of Economics, Massachusetts Institute of Technology, 9 September.
Lim GC, R Dixon and S Tsiaplias (2009), ‘Phillips Curve and the Equilibrium Unemployment Rate’, Economic Record, 85(271), pp 371–382.
Lowe P (2018), ‘Regional Variation in a National Economy’, Address to the Australia-Israel Chamber of Commerce (WA)), Perth, 11 April.
Lowe P (2021), ‘The Labour Market and Monetary Policy’, Address to the Economic Society of Australia (Qld), Online, 8 July.
Lucas RE Jr (1973), ‘Some International Evidence on Output-Inflation Tradeoffs’, The American Economic Review, 63(3), pp 326–334.
Mankiw NG and R Reis (2002), ‘Sticky Information versus Sticky Prices: A Proposal to Replace the New Keynesian Phillips Curve’, The Quarterly Journal of Economics, 117(4), pp 1295–1328.
McLeay M and S Tenreyro (2020), ‘Optimal Inflation and the Identification of the Phillips Curve’, in MS Eichenbaum, E Hurst and JA Parker (eds), NBER Macroeconomics Annual 2019, 34, University of Chicago Press, Chicago, pp 199–255.
Moretti E (2011), ‘Local Labour Markets’, in D Card and O Ashenfelter (eds), Handbook of Labor Economics: Volume 4B, Handbooks in Economics, Elsevier, Amsterdam, pp 1237–1313.
Norman D and A Richards (2010), ‘Modelling Inflation in Australia’, RBA Research Discussion Paper No 2010-03.
Petrosky-Nadeau N and L Zhang (2017), ‘Solving The Diamond–Mortensen–Pissarides Model Accurately’, Quantitative Economics, 8(2), pp 611–650.
Phillips AW (1958), ‘The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861–1957’, Economica, 25(100), pp 283–299.
Productivity Commission (2014), Geographic Labour Mobility, Research Report, Productivity Commission, Canberra.
Productivity Commission (2017), Transitioning Regional Economies, Study Report, Productivity Commission, Canberra.
RBA (Reserve Bank of Australia) (2021a), ‘Minutes of the Monetary Policy Meeting of the Reserve Bank Board’, Videoconference – 6 July 2021’.
RBA (2021b), ‘Economic Outlook’, Statement on Monetary Policy, August.
Roberts JM (1995), ‘New Keynesian Economics and the Phillips Curve’, Journal of Money, Credit and Banking, 27(4, Part 1), pp 975–984.
Ruberl H, M Ball, L Lucas and T Williamson (2021), ‘Estimating the NAIRU in Australia’, Treasury Working Paper 2021–01.
Shapiro C and J Stiglitz (1984), ‘Equilibrium Unemployment as a Worker Discipline Device’, The American Economic Review, 74(3), pp 433–444.
Stiglitz J (1997), ‘Reflections on the Natural Rate Hypothesis’, Journal of Economic Perspectives, 11(1), pp 3–10.
Stimson R, W Mitchell, M Flanagan, S Baum, T-K Shyy (2016), ‘Demarcating Functional Economic Regions across Australia Differentiated by Work Participation Categories’, Australasian Journal of Regional Studies, 22(1), pp 27–57.
Tolbert CM and M Sizer (1996), ‘U.S. Commuting Zones and Labor Market Areas: A 1990 Update’, U.S. Department of Agriculture, Economic Research Service, Rural Economy Division Staff Paper No AGES-9614.
Acknowledgements
For helpful comments and suggestions, we thank Natasha Cassidy, Keaton Jenner, Callum Jones, Gianni La Cava, Gabriela Nodari, Matthew Read, John Simon and seminar participants at the Reserve Bank of Australia. Some of the findings of this RDP were discussed in Lowe (2021). The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia. The authors are solely responsible for any errors. Our programs and publicly available data are available at <https://www.rba.gov.au/publications/rdp/2021/2021- 09/supplementary-information.html>.
Footnotes
Debelle and Vickery showed that, in a horse race, a nonlinear Phillips curve specification outperformed a linear one in several respects. Most importantly, the nonlinear specification generated estimates for the non-accelerating inflation rate of unemployment (NAIRU) that looked more sensible than those from a linear model. Their specification was largely based on that of Debelle and Laxton (1997). [1]
Economic theory suggests that aggregate inflation (in prices and wages) and unemployment outcomes are determined in equilibrium with monetary policy, while the estimates of the Phillips curve at the regional level abstract from the conduct of monetary policy (Fitzgerald et al 2020). As such, using our region-level evidence to directly infer how aggregate wages growth will respond as the unemployment rate declines is only valid, strictly speaking, if monetary policy is completely exogenous. A useful exercise for future research would be to take our estimates of the slope of the wage Phillips curve and use those in a model with a monetary policy rule (or otherwise endogenous monetary policy). In that general equilibrium model you could then trace out the relationship between unemployment, wages, and inflation in a way that is consistent with the regional evidence but also respects the endogeneity issue. [2]
Data limitations also dictate our focus on wage Phillips curves – high-quality price data are not available in Australia at the local labour market level. [3]
The NAIRU is the unemployment rate consistent with inflation being equal to long-run inflation expectations. It is not observable and has to be estimated. The RBA's current approach is to update the NAIRU estimate based on incoming data on unemployment, labour costs and inflation using a Phillips curve framework that treats the NAIRU as an unobserved variable (Cusbert 2017). [4]
Since Friedman (1968), theorists have derived equations that are broadly similar to Equation (1) from models in which price setters have incomplete information (e.g. Lucas 1973; Mankiw and Reis 2002) or nominal prices are sticky (e.g. Roberts 1995). [5]
See Cusbert (2017) for a discussion in the Australian context. [6]
Theoretical models predict that downward nominal wage rigidity can lead to a nonlinear (convex) relationship between inflation and unemployment in both the long run (Akerlof et al 1996) and short run (Daly and Hobijn 2013). Daly and Hobijn also argue that these rigidities cause recessions to result in substantial pent-up wage deflation. [7]
Using job-level data from a private sector survey, Dwyer and Leong (2000) find strong evidence of downward nominal wage rigidity in Australia in the period 1987–99. Charlton (2003) finds downward rigidity in Australian base wages. [8]
See Dupasquier and Ricketts (1998) for a discussion of capacity constraint-driven Phillips curve convexity and its implications for monetary policy. [9]
Although the majority of papers deal with a convex Phillips curve, one branch of the literature (e.g. Stiglitz 1997) posits that a concave Phillips curve could arise due to asymmetric price adjustment under imperfect competition. The idea is that under monopolistic competition, firms might lower prices to undercut rivals when the economy is slowing (and unemployment is high), but will be reluctant to raise prices when demand is strong (and unemployment is low). [10]
The Australian Treasury also uses a nonlinear Phillips curve specification in its medium-term economic projection framework (e.g. Chua and Robinson 2018) and to estimate the NAIRU (Ruberl et al 2021). [11]
These calculations pertain to the slope of the short-run Phillips curve. The slope of the long-run price Phillips curve can be obtained by multiplying the short-run slope estimates by a scaling factor of 1.25 – the result of dividing the short-run slope of the curve by 1 minus the coefficient on lagged inflation from Cassidy et al (2019). In the case of the wage Phillips curve, the appropriate scaling factor is closer to 1.5 (see Appendix A). [12]
Figure 4 presents the RBA aggregate model-implied slope of the wage Phillips curve, assuming the NAIRU is fixed at 4.5 per cent. Allowing the NAIRU to vary over time (as it does in practice in the RBA's Phillips curve models) yields a qualitatively similar slope profile, although the magnitudes are a little larger, particularly over the first half of the time period, reflecting the drift lower in the RBA's central estimate of the NAIRU over the past two decades (see Figures A1 and A2). [13]
One of our colleagues, Tom Cusbert, recently carried out such an exercise using time series data and considering a range of different nonlinear specifications. He finds that Debelle and Vickery's functional form provides a good fit to the post-1968 data. This analysis, in the form of an internal RBA briefing note, is available in our supplementary information <https://www.rba.gov.au/publications/rdp/2021/2021-09/supplementary-information.html>. [14]
Hazell et al (2020) provide a different explanation for the finding that regional Phillips curve slope estimates tend to be larger than aggregate ones, which we discuss in Section 7.2.3. [15]
We describe the McLeay and Tenreyro logic here because it is simple and intuitive. Fitzgerald et al (2020) arrive at a similar conclusion (that, where monetary policy is set to achieve an inflation-targeting mandate, aggregate data is uninformative as to the structural Phillips curve relationship) using a general reduced-form model that does not depend on the nature of the shock applied. [16]
Variability of the domestic component of inflation has declined substantially [since the introduction of inflation targeting], and much of the variation in CPI inflation is now caused by imported shocks, such as commodity price and exchange rate changes. Stabilisation of the domestic component of inflation has weakened the relationship between inflation and domestic economic conditions … (p 24)[17]
An example of something that can affect inflation at policy-relevant horizons, other than the simple pressure of demand, might be the direct impact on CPI inflation of movements in the exchange rate. [18]
The time fixed effects ‘difference out’ the effects of any variables that vary uniformly across all regions over time. [19]
The models include the ‘trend’ measure developed by Cusbert (2017), which extracts a common signal from the range of survey and financial market measures of inflation expectations available in Australia. [20]
The price and wage Phillips curves used in the RBA's forecasting process are estimated over the 1993–2019 and 1998–2019 periods respectively. The RBA's preferred measure of wages growth – the WPI – has only been compiled by the ABS since 1998. Although the preferred price and wage inflation models used by the RBA are run over the post-inflation-targeting period, some of the inputs are generated over a longer sample period. In particular, the NAIRU and trend measure of inflation expectations are themselves jointly estimated using a state-space Phillips curve framework beginning in 1968 (see Cusbert (2017)). [21]
Including region fixed effects also accounts for any permanent differences in long-run inflation expectations across regions. [22]
See Cusbert (2017) for a discussion and references to relevant literature. [23]
This will also occur if the Phillips curve model uses the unemployment rate rather than the unemployment gap. An aggregate model that includes the unemployment rate rather than the unemployment gap is likely to generate a slope estimate that is biased toward zero, given that the national unemployment rate was ‘chasing the NAIRU down’ for much of the post-2000 period. In this situation, what the regression would be picking up is shifts in the curve, rather than movements along a fixed curve. [24]
Although SA3s may appear like a suitable intermediate option, they have the same limitations as SA2s in major cities and SA4s in regional areas. SA3s are also designed with administrative boundaries, rather than labour markets, in mind. [25]
The scope of these data includes anyone who lodged individual tax returns within 16 months of the end of the financial year or who received pay as you go (PAYG) payment summaries from an employer. We compile these data using a number of ABS releases, including ‘Personal Income in Australia’, ‘Estimates of Personal Income for Small Areas’ and ‘Experimental Estimates of Personal Income for Small Areas, Taxation and Income Support Data’. The data for 2004/05 and earlier are available for Statistical Local Areas, which we correspond to SA2s using correspondence files provided by the ABS (please see our online supplementary information files for more detail). [26]
Our analysis excludes region–year observations with fewer than 100 individuals contributing to the annual wage data. [27]
The WPI is published both excluding and including bonuses, although only the excluding bonuses series is available at the state level. [28]
The share of regions with unemployment rates below 4 per cent ranged from a low of 10 per cent in the late 1990s and early 2000s, to a high of 50 per cent in the mid 2000s mining boom. [29]
We show a binned scatter rather than a regular scatter of all region–year observations because the latter are noisy, particularly for smaller regions. [30]
Averages are weighted by regional population to be consistent with the regression analysis. [31]
The longer-term slope of the Phillips curve is equal to . We use contemporaneous unemployment rather than lagged unemployment (which is used in the RBA's aggregate model) on the right-hand side because our data are annual frequency. [32]
As McLeay and Tenreyro (2020) point out, inflation-targeting central banks usually target consumer price inflation rather than wage inflation. If the central bank responds to shocks that affect price inflation but do not directly affect wage inflation, that response will not induce a correlation between the unemployment gap and the error term in the wage Phillips curve. In that case, the slope of the wage Phillips curve will be estimated consistently. Bias will only arise if the central bank leans against shocks that affect both prices and wages. [33]
Aggregate time series estimates of the slope of the wage Phillips curve for the United States range from –0.38 to –0.40 depending on the measure of hourly wages used (Hooper et al 2019). [34]
With the exception of the additional spline terms, the model is the same as specification (B) in Table 2. [35]
Changes in the NAIRU and inflation expectations over time will shift the Phillips curve, but have no bearing on our conclusions as to its slope and curvature. When the unemployment rate is equal to the NAIRU, price inflation will be equal to long-run inflation expectations. However, with a positive rate of productivity growth, wages will grow at a faster rate than prices, all else being equal. [36]
See Dupont (2002) for a description of restricted cubic spline models. While we place the three kinks at the 23rd, 53rd and 80th percentiles (to be consistent with Figure 7), it is more common to place those kinks at the 10th, 50th and 90th percentiles. However, we find that our results are virtually unchanged when we adopt the 10–50–90 approach. [37]
The annualised estimated coefficient is –1.9. [38]
As we discuss in Section 9, the findings of our analysis were incorporated into in the forecast scenarios for wage and price inflation presented in RBA (2021b). [39]
The coefficients on the unemployment rate and interaction terms are –2.83 (0.658) and 0.13 (0.031), respectively (standard errors in parentheses). These estimates suggest that a region that moves from the 25th to 75th percentile of the distribution of ‘award share’ would see the slope of its regional Phillips curve flatten from –0.37 to –0.17. [40]
Debelle and Vickery (1998) find that migration does play a role in equalising labour market conditions between states, although the process takes some time. The Productivity Commission (2014) found evidence that workers move across local labour markets in response to differentials in wage and unemployment rates, but the effects are not large, especially when applied to the typical population gross flows. In 2016/17, only 3½ per cent of households moved more than 50 kilometres from their previous address (Lowe 2018). Survey data suggest that less than 40 per cent of those moves were for work-related reasons, with family, housing or other personal reasons being more important factors (Productivity Commission 2014, Figure 5.9). [41]
The ‘trend’ expectations variable employed in the RBA models uses a range of short- and long-term market- and survey-based measures to extract a common signal of long-term inflation expectations, after controlling for each measure's co-movements with recent inflation (see Cusbert (2017) and Cassidy et al (2019)). [42]
The WPI is designed to measure changes in wage rates for a given quantity and quality of labour. The index is constructed by the ABS by comparing the wage for a given job to the previous quarter; adjustments are made to exclude any changes in wages resulting from changes in the nature of the job or the quality of the work performed. It is constructed for a fixed basket of jobs, so by design it should be unaffected by changes to the composition of the labour force. [43]
The p-values for these coefficient estimates are 0.108 and 0.006, respectively. These regression estimates are based on a common sample (1999–2018) and use a model that includes time and state fixed effects. We find that the coefficient estimates (including on the spline term) are also very similar when we allow for a kink in the curve at 4 per cent. [44]
The specification with both the level and change in the unemployment rate contains exactly the same information as a specification with the current and first lag of the unemployment rate (Gordon 1997). To see this, note that Equation (3) augmented with a lag of the unemployment rate can be rearranged to obtain the expression with a speed limit term This also shows that, in a specification with the speed limit control, the coefficient on the unemployment rate is interpreted as the two-period dynamic effect of the unemployment rate on wages growth. For example, the coefficient on the unemployment rate of -0.20 (second column of Table 3) indicates that a 1 percentage point decrease in the unemployment rate in the current and previous year is associated with a 0.2 percentage point increase in wages growth. [45]
Although the nonlinearity imposed by the RBA's wage Phillips curve model has not changed since Debelle and Vickery (1997), the model is periodically assessed and adjusted as part of the internal RBA forecast review process. Here we present the current model specification. [46]
Some SA2s represent unpopulated areas, such as airports, major commercial and industrial zones, national parks, defence land, urban parks, and sporting precincts. We combine these SA2s with their closest populated SA2. [47]
This calculation expresses the commuting ties between two areas with respect to the smaller of the two areas. In a few rare cases, the sum of the workers commuting between SA2s is greater than the smaller SA2's resident labour force, in which case we set Dij to 0.001. [48]
Following Tolbert and Sizer (1996), we use an average-linkage hierarchical clustering algorithm. [49]
When forming clusters, the algorithm is agnostic about whether SA2s are located next to each other (i.e. contiguous) or not. For example, if fly-in-fly-out workers are commuting long distances it is possible that distant SA2s could form a cluster. However, this rarely happens in practice given that such commuting patterns are atypical. [50]
By itself, the cluster analysis procedure offers little guidance for choosing the ‘optimal’ cut-off point. However, we can use other information to guide this choice. Theory suggests that variables such as wages growth, employment growth and housing price growth should be highly correlated across geographic areas within each local labour market (and less correlated across different local labour markets). As such, to help us choose an appropriate cut-off point we compare the average within-cluster correlation for these economic variables for every possible cut-off point. In addition to these correlations, we consider the average inbound and outbound commuting rates at every possible cut-off value. On these metrics, a cut-off of 0.98 produced reasonable results compared to other possible cut-off values. Although a higher cut-off would lead to a set of labour markets with lower inflow and outflow shares on average, this needs to be balanced against the fact the resultant labour markets would comprise regions with less synchronised market conditions. We also observe that our preferred local labour markets classifications look reasonable when plotted on a map. [51]
These studies also apply hierarchical clustering algorithms to journey to work data from the 2011 Census. [52]
We omit the lagged wages growth terms from the specification to increase comparability with Hazell et al's specification. Including lagged wages growth makes little difference to the conclusions in this appendix. [53]
The impact of this adjustment is far smaller than found by Hazell et al, who find that the implied slope of the Phillips curve falls from 0.112 to 0.0062 when accounting for persistence in unemployment fluctuations. [54]