RBA Annual Conference – 2006 Will China Eat Our Lunch or Take Us to Dinner? Simulating the Transition Paths of the US, EU, Japan and China Hans Fehr, Sabine Jokisch and Laurence J Kotlikoff[1]
Abstract
This paper develops a dynamic, life-cycle, general equilibrium model to study the interdependent demographic, fiscal and economic transition paths of China, Japan, the United States and the European Union. Each of these countries/regions is entering a period of rapid and significant population ageing that will require major fiscal adjustments. But the ageing of these societies may be a cloud with a silver lining coming, in this case, in the form of capital deepening that will raise real wages.
In a previous model that excluded China we predicted that tax hikes needed to pay benefits during the developed world's demographic transition would lead to a major capital shortage, reducing real wages per unit of human capital over time by one-fifth. A recalibration of our original model that treats government purchases of capital goods as investment rather than current consumption suggests this concern was overstated. With government investment included, we find much less crowding-out over the course of the century and only a 4 per cent long-run decline in real wages.
Adding China to the model further alters, indeed, dramatically alters, the model's predictions. Even though China is ageing rapidly, its saving behaviour, growth rate and fiscal policies are currently very different from those of developed countries. If successive cohorts of Chinese continue to save like current cohorts, if the Chinese government can restrain growth in expenditures and if Chinese technology and education levels ultimately catch up with those of the West and Japan, the model's long run looks much brighter. China eventually becomes the world's saver and, thereby, the developed world's saviour with respect to its long-run supply of capital and long-run general equilibrium prospects. And, rather than seeing the real wage per unit of human capital fall, the West and Japan see it rise by one-fifth by 2030 and by three-fifths by 2100. These wage increases are over and above those associated with technical progress, which we model as increasing the human capital endowments of successive cohorts.
Even if the Chinese saving behaviour (captured by its time preference rate) gradually approaches that of Americans, developed-world real wages per unit of human capital are roughly 17 per cent higher in 2030 and 4 per cent higher at the end of the century. Without China they'd be only 2 per cent higher in 2030 and, as mentioned, 4 per cent lower at century's end.
What's more, the major short-run outflow of the developed world's capital to China predicted by our model does not come at the cost of lower wages in the developed world. The reason is that the knowledge that their future wages will be higher (thanks to China's future capital accumulation) leads our model's workers to cut back on their current labour supply. So the short-run outflow of capital to China is met with a commensurate short-run reduction in developed-world labour supply, leaving the short-run ratio of physical capital to human capital, on which wages positively depend, actually somewhat higher than would otherwise be the case.
Our model does not capture the endogenous determination of skill premiums studied by Heckman, Lochner and Taber (1998). Doing so could well show that trade with China, at least in the short run, explains much of the relative decline in the wages of low-skilled workers in the developed world. Hence, we don't mean to suggest here that all US, EU, and Japanese workers are being helped by trade with China, but rather that trade with China is, on average, raising the wages of developed-world workers and will continue to do so.
The notion that China, India and other developing countries will alleviate the developed world's demographic problems has been stressed by Siegel (2005). Our paper, although it includes only one developing country – China – supports Siegel's optimistic long-term macroeconomic view. On the other hand, our findings about the developed world's fiscal condition are quite troubling. Even under the most favourable macroeconomic scenario, tax rates will rise dramatically over time in the developed world to pay baby boomers their government-promised pension and health benefits. As Argentina has so recently shown, countries can grow quite well for years even with unsustainable fiscal policies. But if they wait too long to address those policies, the financial markets will do it for them, often with quite ruinous consequences.
1. Introduction
This paper develops a dynamic, life-cycle, general equilibrium model to study the interdependent demographic, fiscal, and economic transition paths of China, Japan, the US, and the EU. Each of these countries/regions is entering a period of rapid and significant ageing of the population that will require major fiscal adjustments. Understanding how national ageing and the fiscal reaction to national ageing will affect the macroeconomies of these regions is important. If the macroeconomic response is favourable, governments can do less and take more time to deal with what's coming. If the opposite is true, governments must do more and do it more quickly.
Our past research (Fehr, Jokisch and Kotlikoff 2004a, 2004b, 2005) suggested an unfavourable macroeconomic response to national ageing arising from a growing shortage of physical capital relative to human capital. This long-term capital shortage sufficed to reduce the model's real wage per unit of human capital by 20 per cent over the course of the century. The model's predicted major decline in physical capital per unit of human capital is due to the model's predicted major rise in payroll and income tax rates. These tax hikes, in turn, reflect the need to pay pension and health care benefits to increasingly older populations. As originally stressed by Feldstein (1974), raising taxes on workers to make transfers to the elderly reduces the amount of capital workers individually and collectively can and will accumulate.
But our earlier studies, with their dismal forecasts that the interaction of ageing and huge fiscal commitments to the elderly will undermine the macroeconomies of the developed world, omitted two issues. Both of these issues are taken up here, and both militate against a severe capital shortage.
The first is government investment. In our prior studies we treated all government purchases as current consumption. There is some logic for doing so, since many so-called government investment goods (for example, tanks, office buildings to house bureaucrats, space vehicles) may make little or no contribution to a nation's output and productivity and, indeed, may do the opposite. On the other hand, a major share of government investment, be it in constructing roads, erecting schools or building research labs, does seem to be productive.
Treating what governments call investment as investment in the model doesn't entirely eliminate the predicted long-term capital shortage, but it does significantly mitigate it. Compared with its 2004 value, the model's real wage per unit of human capital in 2100 is reduced by only 4 per cent rather than by 20 per cent.
The second omission is China. As everyone knows, China is already a major producer of world output. Its GDP now equals roughly one-ninth of US output. China is also absorbing Western and Japanese technology at a rapid pace. This acquisition of technology, in combination with improved education, holds the prospect for ongoing real income growth in China. But, given China's exceptionally high saving rate, more income growth in China means more Chinese saving, which can be invested in the developed world as well as in China.
The potential for China and other developing countries to ‘bail out’ the developed world, at least in terms of its capital needs, has recently been advanced by Jeremy Siegel (2005). But China has a long way to go if it is to play such a role. China's per capita income and wealth levels are currently only a small fraction – probably less than 15 per cent of the developed world's levels. Of course, China has lots of capitas – its population is 2.6 times the combined populations of the US, Japan and the EU. Still, China's current total holdings of wealth appear to be less than one-quarter and could easily be less than one-tenth of total wealth holdings across the four regions.
Moreover, Chinese saving behaviour may change. It's certainly far from what one would expect to see. One would think that having low current income, but the prospect of much higher future income, would lead the Chinese to spend most of what they now produce. But, if official statistics are to be believed, nothing could be further from the truth. According to OECD (2002) data, the Chinese private sector appears to be saving 40 per cent of available private output, defined as net national income minus government purchases of goods and services. This extraordinarily high Chinese private-sector saving rate explains why the Chinese are currently exporting more capital to the rest of the world than they are importing. Based on European Commission (2005) data, the comparable private-sector saving rates in the US, Japan and the EU are only 4 per cent, 11.5 per cent and 11.1 per cent, respectively.
China is also remarkable when it comes to ageing. Like the developed world, China is getting older. But it's projected over the next half century to age much more rapidly than the US, Japan or the EU. This doesn't mean that China will end up older than these regions. It just means it will make the transformation from a relatively young to a very old society much more rapidly than its trading partners in the developed world.
As Table 1 details, only 6.8 per cent of today's Chinese are 65 and older compared with 17.2 per cent in Japan, 16.3 per cent in the EU and 12.3 per cent in the US. In 2050, 23.6 per cent of the Chinese population will be 65 plus. This is larger than the 20.0 per cent elderly share projected for the US, but smaller than the 28.3 and 36.5 per cent shares projected for the EU and Japan, respectively. So the rapidity of China's ageing doesn't reflect where it will end up, but where it is starting.
| Year | 2000 | 2010 | 2020 | 2030 | 2040 | 2050 | 2100 | |
|---|---|---|---|---|---|---|---|---|
| Population projection US | ||||||||
| Fertility rate (number of children per female) | ||||||||
| Model | 2.11 | 2.05 | 2.00 | 1.95 | 1.90 | 1.85 | 1.77 | |
| Official(a) | 2.11 | 2.08 | 2.03 | 1.95 | 1.89 | 1.85 | – | |
| Life expectancy at birth (years) | ||||||||
| Model | 81.7 | 82.1 | 82.5 | 83.0 | 83.4 | 83.8 | 83.8 | |
| Official(a) | 77.1 | 78.3 | 79.1 | 79.9 | 81.0 | 81.6 | – | |
| Total population (millions) | ||||||||
| Model | 276.2 | 307.3 | 340.0 | 366.4 | 385.8 | 400.3 | 442.0 | |
| Official(a) | 285.0 | 314.9 | 344.3 | 370.4 | 391.4 | 408.7 | – | |
| Age structure (per cent of total population) | ||||||||
| <15 | Model | 21.6 | 20.1 | 19.7 | 18.5 | 18.2 | 17.8 | 15.9 |
| Official(a) | 21.8 | 20.5 | 20.0 | 19.3 | 18.5 | 17.9 | – | |
| 15–64 | Model | 66.2 | 67.2 | 64.0 | 61.4 | 61.7 | 62.1 | 60.7 |
| Official(a) | 65.9 | 66.6 | 64.1 | 61.5 | 61.7 | 62.1 | – | |
| 65–90 | Model | 12.2 | 12.7 | 16.3 | 20.1 | 20.2 | 20.1 | 23.3 |
| Official(a) | 12.3 | 12.8 | 15.9 | 19.2 | 19.8 | 20.0 | – | |
| Population projection EU | ||||||||
| Fertility rate (number of children per female) | ||||||||
| Model | 1.46 | 1.53 | 1.60 | 1.67 | 1.74 | 1.82 | 1.82 | |
| Official(b) | 1.58 | 1.61 | 1.68 | 1.77 | 1.84 | 1.85 | – | |
| Life expectancy at birth (years) | ||||||||
| Model | 82.2 | 82.7 | 83.2 | 83.6 | 84.1 | 84.6 | 84.6 | |
| Official(b) | 78.6 | 80.0 | 81.1 | 82.0 | 83.0 | 83.6 | – | |
| Total population (millions) | ||||||||
| Model | 376.4 | 385.8 | 390.9 | 391.1 | 384.1 | 372.1 | 340.6 | |
| Official(a) | 377.3 | 383.2 | 384.4 | 382.8 | 377.8 | 369.8 | – | |
| Age structure (per cent of total population) | ||||||||
| <15 | Model | 16.9 | 15.3 | 14.5 | 14.3 | 14.3 | 14.8 | 16.5 |
| Official(a) | 16.7 | 15.3 | 14.4 | 14.4 | 14.7 | 15.0 | – | |
| 15–64 | Model | 66.9 | 66.9 | 64.7 | 60.8 | 57.7 | 57.2 | 59.7 |
| Official(a) | 66.9 | 66.5 | 64.7 | 60.8 | 57.5 | 56.7 | – | |
| 65–90 | Model | 16.2 | 17.8 | 20.8 | 24.9 | 28.0 | 28.0 | 23.9 |
| Official(a) | 16.3 | 18.2 | 21.0 | 24.7 | 27.8 | 28.3 | – | |
| Population projection Japan | ||||||||
| Fertility rate (number of children per female) | ||||||||
| Model | 1.28 | 1.37 | 1.47 | 1.56 | 1.66 | 1.75 | 1.91 | |
| Official(a) | 1.32 | 1.37 | 1.49 | 1.68 | 1.81 | 1.85 | – | |
| Life expectancy at birth (years) | ||||||||
| Model | 83.8 | 84.6 | 85.4 | 86.2 | 87.0 | 87.8 | 87.8 | |
| Official(a) | 81.6 | 83.5 | 85.1 | 86.6 | 87.7 | 88.1 | – | |
| Total population (millions) | ||||||||
| Model | 126.7 | 128.9 | 127.1 | 121.8 | 114.2 | 108.8 | 84.8 | |
| Official(a) | 127.0 | 128.0 | 125.6 | 121.0 | 115.7 | 109.7 | – | |
| Age structure (per cent of total population) | ||||||||
| <15 | Model | 14.6 | 13.4 | 12.5 | 11.9 | 12.5 | 12.9 | 16.0 |
| Official(a) | 14.6 | 13.6 | 12.4 | 11.8 | 12.6 | 13.0 | – | |
| 15–64 | Model | 68.2 | 64.1 | 59.2 | 58.1 | 55.0 | 52.1 | 56.3 |
| Official(a) | 68.2 | 64.0 | 59.5 | 57.8 | 53.0 | 50.4 | – | |
| 65–90 | Model | 17.2 | 22.5 | 28.2 | 30.0 | 32.5 | 35.0 | 27.7 |
| Official(a) | 17.2 | 22.4 | 28.1 | 30.4 | 34.4 | 36.5 | – | |
| Population projection China | ||||||||
| Fertility rate (number of children per female) | ||||||||
| Model | 1.62 | 1.67 | 1.71 | 1.76 | 1.80 | 1.85 | 2.01 | |
| Official(c) | 1.32 | 1.37 | 1.49 | 1.68 | 1.81 | 1.85 | – | |
| Life expectancy at birth (years) | ||||||||
| Model | 75.8 | 76.7 | 77.5 | 78.4 | 79.3 | 80.2 | 80.2 | |
| Official(c) | 71.5 | 72.6 | 73.8 | 75.3 | 77.1 | 78.7 | – | |
| Total population (millions) | ||||||||
| Model | 1,273.1 | 1,360.7 | 1,455.0 | 1,490.7 | 1,481.3 | 1,430.8 | 1,181.8 | |
| Official(c) | 1,274.0 | 1,354.5 | 1,423.9 | 1,446.5 | 1,433.4 | 1,392.3 | – | |
| Age structure (per cent of total population) | ||||||||
| <15 | Model | 24.6 | 19.5 | 18.3 | 16.5 | 15.6 | 16.3 | 18.5 |
| Official(c) | 24.8 | 19.5 | 18.4 | 16.9 | 15.6 | 15.7 | – | |
| 15–64 | Model | 68.6 | 73.3 | 70.6 | 67.8 | 63.1 | 61.6 | 61.7 |
| Official(c) | 68.4 | 72.2 | 69.7 | 66.8 | 62.1 | 60.7 | – | |
| 65–90 | Model | 6.8 | 7.2 | 11.1 | 15.7 | 21.3 | 22.0 | 19.8 |
| Official(c) | 6.8 | 8.3 | 11.9 | 16.3 | 22.3 | 23.6 | – | |
| (a) UN Population Division (2003), medium variant projections (b) UN Population Division (2003), medium variant projections, Western Europe (c) UN Population Division (2005), medium variant projections |
||||||||
The fact that China, like Japan and the West, is ageing and faces significant fiscal obligations associated with that process suggests that China's inclusion in our model would make little difference to the model's unpleasant prediction of a looming capital shortage. But because of China's much higher rates of growth and saving and because its population is so large, adding China can, as documented below, transform a capital shortage into a capital glut. Whether or not this occurs depends on how China's fiscal policy and saving behaviour evolve. If, over the course of the next 50 years, China adopts fiscal arrangements and saving propensities that are similar to those of developing nations, China will make only a modest contribution to the world's supply of capital, leaving real wages per unit of human capital at the end of this century only about 4 per cent higher than they are today. If, on the other hand, China limits growth in public expenditures and the Chinese people continue to eschew consumption, China will save enough for its own capital needs as well as those of the developed world, leaving real wages per unit of human capital at the end of this century roughly 60 per cent above the current level.
The usefulness of these findings depends, of course, on the realism of our model. Our life-cycle model's features are extensive. The model includes: age-, region- and year-specific fertility and mortality rates; lifespan uncertainty; age-, region- and year-specific pension, disability, health care and other government transfer policies; region- and year-specific government purchases of goods and services; region-specific levels of debt; high, middle and low earners within each cohort in each region; region-specific personal wage income, capital income, corporate income and payroll taxes; international capital mobility; technological change; quadratic costs of adjusting each region's capital stock; age-specific inheritances; age-specific and unintended bequests; intertemporally separable Constant Elasticity of Substitution (CES) utility functions in consumption and leisure; region-specific Cobb-Douglas production functions; the presence of children's utility in parents' utility functions when the children are young; exogenously specified age-, earnings class-, region- and year-specific immigration; and region- and cohort-specific time preference rates.
As with our other three regions, to accommodate Chinese saving behaviour, we've set the Chinese time preference rate to match the current observed saving rate for China. And we've calibrated the multifactor productivity coefficient in the Chinese production function to match the current observed Chinese relative wage. The big questions with respect to China's calibration, however, are not how to treat current saving preferences and technology, but rather how to model future saving preferences and technology.
Consider first the issue of technology. It seems reasonable to believe that the level of Chinese technology will converge to that of the West. The unknown is the rate of convergence. In this study our base case assumes that the Chinese multifactor productivity coefficient rises gradually, reaching the US, Japanese and EU levels by mid century. But we also consider slower and faster rates of technological convergence.
Now consider modelling future Chinese saving behaviour. Here we examine two alternative assumptions. The first is that the Chinese time preference rate remains fixed through time at the very low rate needed to match the current Chinese saving rate. The second is that successive cohorts of Chinese gradually adopt Western saving behaviour such that the Chinese born in 2050 and thereafter have the same time preference rate as Americans in 2004.
2. Our Model and its Predecessors
The development of dynamic life-cycle simulation models was stimulated by Feldstein's (1974) article contending that government pension systems lower national saving. Early dynamic analysis of government pension programs and other policies include Kotlikoff (1979), Summers (1981), Auerbach and Kotlikoff (1983, 1987) and Seidman (1986). More recent papers have considered the importance of land, earnings uncertainty, political economy considerations, liquidity constraints, different options for funding social security and human capital decisions. These studies include Hubbard and Judd (1987), Raffelhüschen (1989, 1993), Imrohoroglu, Imrohoroglu and Joines (1995, 1999), Kotlikoff (1996), Huang, Imrohoroglu and Sargent (1997), Heckman et al (1998), Kotlikoff, Smetters and Walliser (1998a, 1998b, 1999, 2002), Cooley and Soares (1999a, 1999b), De Nardi, Imrohoroglu and Sargent (1999), Huggett and Ventura (1999), Bohn (2001), Nishiyama and Smetters (2003), Smetters and Walliser (2004) and Fehr and Habermann (2005).
This model, like our previous ones, builds on Auerbach-Kotlikoff's (1987) overlapping generation (OLG) model. Auerbach and Kotlikoff also simulated demographic transitions, but their model assumed that all agents gave birth at a fixed age, died and bequeathed at a fixed age and received inheritances at a fixed age. Kotlikoff, Smetters and Walliser (2001) advanced the Auerbach-Kotlikoff model by incorporating age-specific fertility and inheritance, lifespan extension, intragenerational earnings heterogeneity, and additional fiscal institutions. Fehr et al (2004a, 2004b, 2005) included lifespan uncertainty as well as bequests arising from incomplete annuitisation. They also introduced multiple regions with international capital mobility and immigration.
As in Kotlikoff et al (2001), our model features monozygotic reproduction with agents in their child-bearing years giving birth each year to fractions of children. This means of finessing marriage and family formation permits us to incorporate changes through time in age-specific fertility rates and to closely line up our model's age-specific population shares to those forecast for the four regions.
We assume that agents care about their children's utility when they are young and, as a consequence, make consumption expenditures on behalf of their children (pay for their consumption), but only when the children are young. We also assume that agents die with realistic mortality probabilities starting at age 68. Agents fully appreciate the uncertainty of their longevities and maximise, at any point in time, their expected remaining lifetime utilities. The inclusion of lifespan uncertainty permits a realistic modelling of bequests and inheritances.
We generate bequests by assuming that agents fail to annuitise their assets in old age. Hence, when they die, they leave undesired bequests to their children. Since agents die at different ages and have children of different ages, their heirs also inherit at different ages. Agents who were born when their parents were young receive inheritances later in their life than do their younger siblings. Finally, uninsurable lifespan uncertainty leads agents to gradually reduce their consumption in old age.
Our model also includes capital adjustment costs. As is well known, these costs can drive temporary wedges between the marginal products of capital in different regions and lead the market values of capital assets to temporarily differ from their replacement costs. Thus inclusion of adjustment costs in the model generates what amounts to regional stock markets and permits us to explore how population ageing affects world stock prices through time.
A final, but very important, feature of our framework is its intra-cohort disaggregation. As in Kotlikoff et al (2001), we consider three income classes within each generation, each with its own earnings ability. Immigrants are also split into these income classes permitting us to simulate the arrival of immigrants with different stocks of human and physical capital.
The following sub-sections present the general structure of our model. A more detailed description of the three-country model is provided in Fehr et al (2003).
2.1 Demographics
Each region is populated by households who live at most to age 90. Consequently, there are 91 generations with surviving members at any point in time. The individual life cycle of a representative agent is described in Figure 1. Between ages 0 and 20 our agents are children who earn no money and are supported by their parents. At age 21 our agents leave their parents and go to work. Between ages 23 and 45 our agents give birth to fractions of children at the beginning of each year, that is, the first (fraction of) children are born when the agents are 23 and the last are born when they are age 45. An agent's first-born children (fractions of children) leave home when the agents are age 43, while the last-born leave when the agents are age 66. Our agents die between ages 68 and 90. The probability of death is 1 at age 91. Children always outlive their parents, meaning that parents always outlive grandparents. To see this, note that if a parent reaches age 90, his or her oldest children will be 67. These are children who were born when the parent was age 23.

In each year, new immigrants in each skill and age group arrive with the same number and age distribution of children and the same level of assets as natives of the identical skill and age. Since the demographic structure has the same general form in all four regions, it suffices to discuss a representative region and omit region indices.
To specify the current and future demographic structure of each region we start with
year-2000[2]
age-specific population  and age-specific net immigration
and age-specific net immigration  counts.
counts.
In constructing existing as well as future age-population counts, we have to link each initial cohort between the ages of 1 and 68 to those of their parents who are still alive. The reason is that children receive bequests from their parents, and the levels and timing of these inheritances depend on the ages of their parents. This link is achieved by applying past fertility rates to each cohort under age 69 in year 2000. If, for example, 15 per cent of the parents of newborns in 1980 were 25 years old, then 15 per cent of the 20-year-olds in year 2000 are assigned to parents aged 45.
In addition, each cohort is split into three income classes k. Specifically, we assume that 35 per cent of each cohort belong to the lowest income class, 10 per cent to the top income class and the remaining 55 per cent to the middle income class. We denote the population vector for year t as N(a,t,s,k) where a = 1,…,90, s = 23,…,45, k = 1,2,3. The term s references the age of the parent at the time of birth of agents aged a in year t.
To determine the evolution of the population in each region over time, we applied region-, age- and year-specific mortality and fertility rates to the cohorts alive in year 2000 as well as to their children as they reach their ages of fertility and mortality. In the baseline path the exogenous current and future mortality and fertility rates follow the medium variant of the United Nations population projection (UN Population Division 2003 for the US, EU and Japan; UN Population Division 2005 for China).
According to this projection, mortality rates will decline in all four regions over time. Consider the Japanese, whose 2000 life expectancy equalled 81.6 years. According to official projections, Japan's life expectancy in 2050 will reach 88.1 years. The Japanese, who now have a life expectancy 4.5 years higher than Americans and 3.0 years higher than EU citizens, will continue to maintain their longevity lead through time. Indeed, projected 2050 US life expectancy doesn't even exceed current Japanese life expectancy! In China, life expectancy is now a full 10 years lower than life expectancy in Japan. And this 10-year gap is projected to continue for the next half century.
Table 1 shows our agents' life expectancies at birth in the baseline path, which is kept constant after the year 2050. The respective numbers are higher than the actual values, since our model's agents don't die prior to age 68. However, the model's life expectancies conditional on reaching age 60 are close to those reported by the UN Population Division (2005).
Total fertility rates currently equal 2.1, 1.3, 1.6 and 1.5 in the US, Japan, China and the EU, respectively. Nevertheless, the UN expects fertility rates in all four regions to converge to 1.85 children by 2050. This path of fertility rates is also shown in Table 1. In the baseline path, we assume annual net immigration of 1 million per year in the US, 450,000 in the EU and 54,000 in Japan. Net immigration into China is negative; the number of net emigrants is fixed at its current value of 390,000 people per year. Given the population age structure in year 2000 as well as projected future fertility, mortality and net immigration rates, we compute the population vector N(a,t,s,k) for the years t between 2001 and 2050. After the year 2050, fertility rates are endogenously adjusted in order to achieve zero population growth and a stable population age structure. Since net immigration is positive in the US, the EU and Japan, the fertility rates which stabilise the population post-2050 are below 2.0. Equivalently, the fertility rates in China are set above 2.0 after 2050 due to net emigration.
Table 1 also shows projected changes over time in total populations and population age structures. Due to high fertility and net immigration rates, the US population is projected to increase from 276 million in 2000 to 442 million in 2100. In Europe, the population falls over the century from 376 million to 341 million, and in Japan, the population falls from 127 million to 85 million. The Chinese population decreases by even more – from 1.3 billion to 1.2 billion.
As one would expect, the population share of those 65 and older increases in all four regions. There are, however, big differences in the ageing process across the four regions. First, in the US and China the absolute decrease in the shares of the young population through 2050 are almost the same as for the working-age population. In contrast, the EU and Japan experience much larger absolute declines in the share of the population that is of working age. Second, the share of the elderly increases to a much larger extent in Japan and China compared to the US and the EU.
Table 1 indicates that our model's demographic machinery does a remarkably good job of matching official projections for the four regions both with respect to the absolute number and age compositions of their respective populations. We now describe this machinery in more detail.
The total number of children of an agent aged a in income class k in year t is recorded by the following function

where u = max(0; a−45) and m = min(20; a−23). Recall that agents younger than 23 have no children and those over 65 have only adult children, that is KID(a,t,k) = 0 for 0 ≤ a ≤ 22 and 66 ≤ a ≤90. Agents between these ages have children. Take, for example, a 30 year-old agent. Such an agent has children who were born in the years (a−j) since she/he was 23. In year t, these children are between age 0 ≤ j ≤ 7. The KID-function (1) sums the total number of children of the respective parent-income class generation and divides it by the total number of parents of age a in year t who belong to income class k. This function takes into account that the family's age structure will change over time due to changing fertility. This approach permits the distribution of births by the ages of parents to change over time – an important improvement relative to the birthing process stipulated in Kotlikoff et al (2001).
2.2 The household sector
As previously mentioned, we do not distinguish between natives and immigrants once the immigrants have joined the native earnings- and age-specific cohorts. The model's preference structure is represented by a time-separable, nested, CES utility function. Remaining lifetime utility U(j,t,s,k) of a generation of age j at time t whose parents were age s at time of birth and who belong to income class k takes the form

where V(j,t,s,k) records the agent's utility from her/his own goods and leisure consumption and H(j,t,s,k) denotes the agent's utility from the consumption of her/his children. The two sub-utility functions are defined as follows:


where c(a,i,s,k) and l (a,i,s,k)denote consumption and leisure, respectively, and i is defined as i = t + a − j. The children's consumption of income class k parents who are age a in period i and whose parents were age s at the time of their birth is defined as cK(a,i,s,k). Note that the number of children is independent of the grandparent's age at the time of the birth of the parents.
Since lifespan is uncertain, the utility of consumption in future periods is weighted by the survival probability of reaching age a in year i

which is determined by multiplying the conditional survival probabilities from year t (when the agent's age is j) up to year i. Note that d(j,t) is the mortality probability of an agent age j in year t. The parameters θ, ρ, α and γ represent the ‘pure’ rate of time preference, the intratemporal elasticity of substitution between consumption and leisure at each age a, the leisure preference parameter and the intertemporal elasticity of substitution between consumption and leisure in different years, respectively.
In maximising utility, agents choose their demand for leisure subject to the constraint that leisure in each period not exceed h(a,i), which is the time endowment. The determination of the shadow values of these leisure constraints, when these constraints are binding, is included as part of the maximisation. To ensure that agents retire by a designated maximum retirement age, we set the net wage at that age and thereafter to zero.
Given the asset endowment a(j,t,s,k) of the agent in year t, maximisation of (2) is subject to a lifetime budget constraint defined by the sequence:

where r(t) is the pre-tax return on savings and I(j,t,s,k) denotes the inheritance the agent receives in year t. When the parents die between age 68 and 90, their remaining assets are split between their children. Consequently, inheritances of agents who are age j in year t and whose parents were age s at their birth are defined by:

The numerator defines the aggregate assets of income class k parents who die in year t at age j + s. The denominator defines these parents' total number of children who are between ages j+s−45 and j+s−23 in year t. The receipt of inheritances requires us to distinguish members of each cohort according to the ages of their parents at birth. The parents' ages at death determine when the children receive their inheritances. While the oldest children (born when their parents are age 23) receive their inheritances between ages 45 and 67, the youngest children (born when their parents are age 45) receive their inheritances earlier in life, between ages 23 and 45.
As in Altig et al (2001) and Kotlikoff et al (2001), we assume that technical progress causes the time endowment h(·) of each successive generation to grow at the rate λ, that is

The proposition here is not that time, per se, expands for successive generations, but rather that each successive generation is more effective in using time to either perform work or enjoy leisure. Treating technical change in this manner is essential to ensure that the economy achieves a long-run steady state. The assumption of labour-augmenting technical change would not, for example, be compatible with a long-run steady state given the nature of the model's preferences. And having the economy achieve a long-run steady state provides, in effect, the terminal conditions needed by our algorithm to solve for the model's equilibrium transition path.
Gross labour income of the agent in year t is derived as the product of her/his labour supply and her/his wage rate. The latter is the product of the gross wage rate w(t) in period t and the age- and class-specific earnings ability.

The middle-income class profile is taken from Auerbach and Kotlikoff (1987). The shift parameters ξ(k) are then applied to derive income-class-specific profiles. Moreover, since technological change is an important determinant of secular growth over the life-cycle, we multiply the profile of the age-specific longitudinal earnings ability by the term involving λ. Hence, the longitudinal age-wage profile is steeper the greater is the rate of technological change.
The net taxes T(j,t,s,k) of an agent in year t consist of consumption, capital income and progressive wage taxes as well as social security contributions net of pension and disability benefits received. Pension, disability insurance and health care average and marginal payroll tax rates differ across agents, due to our assumed ceiling on payroll tax contributions. Each agent's pension benefits depend on her/his pre-retirement earnings history, while health care and disability transfers are provided on a per capita basis to all eligible age groups.
Given individual consumption, leisure, and asset levels of all agents, we can compute aggregate variables. For example, the aggregate value of assets A(t+1) at time t+1 is computed from

Since households die at the beginning of each period, we have to aggregate across
all agents who lived in the previous period in order to compute  (a+1,t +1,k), which we need
for the calculation of bequests, see (7). If we aggregate across agents who
live in period t+1, then we have,
(a+1,t +1,k), which we need
for the calculation of bequests, see (7). If we aggregate across agents who
live in period t+1, then we have,

which includes the assets of the arriving immigrants of period t+1. The difference in the asset aggregates in Equations (10) and (11) arises from the difference in the population counts. Equation (11) uses time t+1 counts, which include immigrants who arrive at the beginning of time t+1, whereas Equation (10) uses time t counts, which include all those who can potentially die and leave bequests at the end of period t.
Finally, the aggregate labour supply, measured in efficiency units, of agents in year t, L(t), is computed from the individual labour supplies, that is

2.3 The production sector
The economy is populated by a large number of identical firms, the total number of which is normalised to unity. Aggregate output (net of depreciation) is produced using Cobb-Douglas production technology, that is

where K(t) is aggregate capital in period t, ε is capital's share in production, and φ is a technology parameter. Since we posit convex capital adjustment costs, the firms' marketable output in year t, Y(t), is given by the difference between gross output and adjustment costs, that is

where ΔK(t) measures investment in year t. The term ψ is the adjustment cost coefficient. Larger values of ψ imply higher marginal costs of new capital goods for a given rate of investment. The installation technology is linear homogeneous and shows increasing marginal cost of investment (or, symmetrically, disinvestment): faster adjustment requires a greater than proportional rise in adjustment costs.
Corporate taxes, Tk(t), are given by

where τk(t) and ε(t) define the corporate tax rate and the immediate share of investment expenditures that can be written off, respectively. Adjustment costs are fully deductible from the tax base, while investment expenditures are partly deductible. Hence, arbitrage between new and existing capital implies that the latter has a price per unit of

Similarly, the arbitrage condition arising from profit maximisation requires identical returns to financial and real investments:

The left side gives the return on a financial investment of amount q(t), while the return on one unit of real capital investment is the net return to capital (which includes the marginal product of capital FK(t) plus the reduction in marginal adjustment costs) and capital gains.
2.4 The government sector
The consolidated government issues new debt ΔB(t) and collects corporate taxes and net taxes from households in order to finance general government expenditures G(t) as well as interest payments on its debt:

With respect to public debt, we assume that the government maintains an exogenously fixed ratio of debt to output. The progressivity of the wage tax system is modeled as in Auerbach and Kotlikoff (1987). Specifically, marginal wage tax rates rise linearly with the tax base.
PY(t) defines the aggregate payroll tax base, which differs
from total labour earnings due to the ceiling on taxable wages. This ceiling
is fixed at 250, 200, 168 and 300 per cent of average income in the US, the
EU, Japan and China, respectively. Aggregate average social security payroll
tax rates  and
and  are computed each period from the relevant budget
constraint for the program and region in question, that is
are computed each period from the relevant budget
constraint for the program and region in question, that is
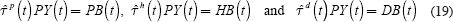
where PB(t), HB(t) and DB(t) are total outlays of the pension, health care, and disability systems, respectively. For China we assume that disability insurance is part of the state pension system. Hence, we do not calculate separate disability insurance payroll tax rates for this country.
Due to contribution ceilings, individual pension, disability and health insurance payroll tax rates can differ from the payroll tax rate (applicable on earnings below the ceiling). Above the contribution ceiling, marginal social security contributions are zero and average social security contributions fall with the agent's income. To accommodate this non-convexity of the budget constraint, we assume that the highest earnings class in each region pays pension and (in the EU, Japan and China) health insurance payroll taxes, up to the relevant ceilings, but faces no pension and no health care payroll taxes at the margin. The other earnings classes are assumed to face the full statutory tax rate on all earnings. The disability payroll taxes in the US, the EU and Japan are modelled in an equivalent manner. However, since there is no ceiling on US Medicare taxes, all earnings groups are assumed to face the health insurance payroll tax at the margin.
If a k-income-class agent, whose parents were s years old at her/his
birth, retires in year z at the exogenously set retirement age  (z), her/his pension benefits Pen(a,i,s,k)
in years i ≥ z when she/he is age a≥
(z), her/his pension benefits Pen(a,i,s,k)
in years i ≥ z when she/he is age a≥  (z) depend linearly on her/his average earnings,
(z) depend linearly on her/his average earnings,
 (z,s,k), during his working
time:
(z,s,k), during his working
time:

The region-specific parameters ω0, ω1 in the US, the EU and Japan were chosen in order to approximate replacement rates relative to individual lifetime earnings as reported in Whitehouse (2002). In China, we assumed a pension-replacement rate of 50 per cent of average pre-retirement earnings. There are little reliable data to assess the accuracy of this replacement rate assumption. But the assumption seems reasonable given the Chinese Government's recent decision to recognise the unfunded liabilities of state-owned enterprises.
General government expenditures G(t) consist of government purchases of goods and services, including educational expenditures and health outlays. Over the transition, general government purchases of goods and services are held fixed as a per cent of national income. Age-specific education and disability outlays are held fixed per capita over the transition with an adjustment for technological change. Age-specific health outlays are also held fixed in per capita terms, but are assumed to grow at twice the rate of technological change during the first 25 years of the transition. Afterwards, the age-specific levels of these outlays grow at the same rate as technological change. Note that while the outlays of the health care systems are treated as government expenditures, disability benefits are modelled as direct transfers to the households. The government's budget constraint, Equation (18), is balanced each year by adjusting the intercept in our linear equation determining the average wage tax rate.
2.5 World equilibrium
Up to now we've described the model for the representative economy. The four regions of the model are, however, connected through the world capital market. A condition of this market is that the value of aggregate world assets equals the market value of the worldwide capital stock plus the value of all outstanding government bonds, that is

2.6 Solving the model
To simulate the model we need, of course, to specify preference, technology and policy parameters. Table 2 reports these values, which, in the case of preference and technology parameters, are mostly taken from Kotlikoff et al (2001).
| Symbol | Value | ||||
|---|---|---|---|---|---|
| US | EU | Japan | China | ||
| Utility function | |||||
| Time preference rate | θ | 0.01 | 0.00 | 0.01 | −0.13 |
| Intertemporal elasticity of substitution | γ | 0.25 | 0.25 | 0.25 | 0.25 |
| Intratemporal elasticity of substitution | ρ | 0.4 | 0.4 | 0.4 | 0.4 |
| Leisure preference parameter | α | 1.5 | 1.5 | 1.5 | 1.5 |
| Production function | |||||
| Technology level | φ | 1.01 | 1.01 | 1.01 | 0.24 |
| Capital share in production | ε | 0.25 | 0.25 | 0.25 | 0.25 |
| Technical progress | λ | 0.01 | 0.01 | 0.01 | 0.01 |
| Policy parameters | |||||
| Consumption tax rate (%) | τc | 10.2 | 23.6 | 14.7 | 20.0 |
| Capital tax rate (%) | τr | 11.0 | 14.0 | 8.0 | 0.0 |
| Corporate tax rate (%) | τk | 12.0 | 18.0 | 16.0 | 0.0 |
| Expensing fraction (%) | ∈ | 0.0 | 20.0 | 40.0 | 0.0 |
| Debt (% of national income) | B/Y | 33.3 | 38.9 | 41.4 | 10.0 |
| Age of retirement (years) | 63 | 60 | 60 | 60 | |
|
Source: authors' calculations |
|||||
The multifactor technology coefficient in the US Cobb-Douglas function was set to generate a US marginal product of labour of 1.0 in the initial year 2004. For the EU and Japan we simply adopted this technology level. For China the technology level was set to achieve a 2004 real wage equal to 15 per cent of the US level. During the transition we gradually adjust China's technology level such that it reaches the developed world's level in 2050.
The time preference rates in the four regions were set so that the model's 2004 ratios of private consumption to national income match the region-specific values reported by the European Commission (2005). The US, EU and Japanese time preferences rates are held fixed through time. But in line with our baseline assumption that the Chinese public will eventually adopt American spending habits, we gradually raise the time preference rate of successive Chinese cohorts so that cohorts that reach adulthood (age 21) in 2030 and thereafter have the time-invariant US time preference rate.
The model's government debt levels in the four regions were chosen to accord with real government interest payments reported by the European Commission (2005) for the year 2004. The maximum ages of retirement are taken from Blöndal and Scarpetta (1998) for the US and the EU, from Whitehouse (2002) for Japan and from the OECD (2002) for China. We set the consumption tax rate, personal capital income tax rate, corporate income tax rate and expensing rate for the US, the EU and Japan in line with the structure of indirect and direct tax revenues reported by the European Commission (2005). We use OECD (2002) data to determine China's consumption tax rate, but assume that China has no personal capital income or corporate income taxes. It may well be that such taxes exist in China, but we have no reliable information to understand their magnitudes.
Our wage tax systems are assumed to be progressive, with the parameters of these tax systems in each region set so as to generate what seem to be realistic average and marginal tax rates, which are reported below.
In calibrating health expenditures in our model, we apply the Japanese age-specific government healthcare expenditure profile for Japan as well as China. In the case of the EU, we use the German profile. For the US, the Medicare program applies only to households aged 65 and older. We assume uniform Medicare expenditures by age. We make the same uniform age-distribution assumption with respect to the disability insurance systems in the US, the EU and Japan, which we assume applies only to those older than 20 and younger than 65.
In the case of the US, the EU and Japan, total social insurance outlays for pensions, disability and health, measured as a share of national income, are set to accord with the values of these totals reported by the European Commission (2005). But we determined the composition of these expenditures according to the three types of benefits using data reported in Docteur and Oxley (2003), European Commission (2003) and OECD (2001) and invoking the assumption for the EU and Japan that their ratios of disability expenditures to pension expenditures are the same as prevails in the US. Note that our baseline path assumes a gradual 20 per cent cut in Japanese pension replacement rates through to 2017, which was recently legislated by the Japanese government. For China our division of social insurance outlays is restricted to pensions plus disability payments, on the one hand, and health expenditures, on the other. Calibration here is based on OECD (2002).
We use the German age-specific education profile for all regions in the model and rescale it to get realistic education outlays in the year 2004 in each region (see below). In addition to these parameter values, our model requires an initial distribution of assets by age and income class for each region. These profiles are region-specific.[3]
To run our model as an open world economy, we also need to specify total world assets and how these assets are distributed across regions. The model's level of total world assets was set to generate a capital-output ratio of 3.0 in our model in the absence of China. Our additional assumption that per capita wealth in China equals 10 per cent of per capita wealth in the developed countries sufficed to pin down the capital-output ratio in the four-region model, namely 2.3.
In our simulations with adjustment costs, for the base year, 2004, we also need to specify the shares of wealth in each country owned by citizens of each region. The reason is that the endogenous determination of capital prices in each region will differentially affect wealth holdings of each region's nationals depending on where they hold their wealth. The data needed to determine the region-specific allocation of each region's wealth holdings are not available. Consequently, we make the following, admittedly crude, assumption. We assume that US, EU, Japanese and Chinese nationals own 70 per cent of the capital installed in their region and that the remaining 30 per cent is owned equally by foreigners from the other three regions. In the case of the US, for example, we assume that the Japanese, EU nationals and Chinese each own 10 per cent of the US capital stock, where these holdings include government claims.
The initial (year 2004) world capital stock, the allocation of this capital stock across regions, the regional ratios of government debt to national income, and the international, intergenerational and intragenerational distributions of assets constitute the initial conditions needed to solve for the perfect foresight general equilibrium transition path of the economy. The algorithm we use to solve the model employs Gauss-Seidel iteration.
Specifically, our algorithm starts with initial guesses for capital stocks and labour supplies in each region for the post-2004 years of the transition. Next we compute from Equation (16) the path of the q's – the region-specific market prices of capital. The path for the world interest rate is derived from the arbitrage condition Equation (17) for the US. Next, region-specific wage rates are computed for each year by setting them equal to their respective marginal products of labour.
The initial region-specific capital values, our working value of q in 2004, and 2004 initial region-specific debt levels suffice to determine total worldwide wealth in 2004 using the world capital market equilibrium condition of Equation (21). These aggregate values are then distributed to the agents of each region based on the initial 2004 region-specific wealth shares and region-specific age-asset profiles.
Given these initial individual asset holdings, our initial guesses of tax rates/tax function parameters and the derived time paths of wage and interest rates, we calculate household consumption, saving and labour-supply decisions. The first-order conditions and lifetime budget constraints determining these decisions are fairly complex and certainly do not have ready closed-form solutions. Part of this complexity arises because of the progressive nature of our assumed wage tax structures, which means that marginal tax rates are themselves endogenous and need to be determined jointly with life-cycle consumption, saving and labour-supply decisions. This is done using Gauss-Seidel iteration. We refer to this as ‘inter-loop’ convergence. As indicated just below, we also use Gauss-Seidel iteration to determine the time path of the economy's macroeconomic variables. We refer to this iteration on macroeconomic variables as ‘outer-loop’ convergence.
The next step in our overall solution algorithm uses the annual revenues and social security benefit payments implied by these household decisions to update annual tax rates/tax parameters. We also update the model's region-specific time paths of government debt. These updates are based on Equations (18) and (19).
Aggregating individual labour supplies in each year provides new time paths of aggregate region-specific labour supplies. Determining new time paths of capital stocks in each region is a bit more involved. First, we use year-2004 wealth holdings plus agent-specific saving decisions to determine agent-specific asset holdings in each year during the transition. Second, we aggregate agent-specific assets at each date to determine a time path of aggregate world-wide asset holdings. Third, we use Equation (17) to substitute out for ΔK(t)/K – the percentage change in capital – in Equation (16). Finally, we equate the interest rates in Japan, the EU and China to that in the US using the modified versions of Equation (17). Given our working values of the q's, this provides us with three equations in a given year to solve for the four region-specific capital stocks. The fourth equation comes from the worldwide capital market condition, which, given our working values of q's and debt, provides another equation in the four unknown region-specific capital stocks.
The new values for the aggregate supplies of capital and labour in each region in each year are then weighted with the initial guesses of these variables to form new guesses of their time paths. The algorithm then iterates until the region-specific time paths of capital stocks and labour supplies converge to a fixed path.
We give our economy 300 years to reach a steady state. In fact, our model reaches a steady state to many decimal places decades prior to year 300. It also converges very tightly around the equilibrium transition path. However, when we include capital adjustment costs, finding the equilibrium transition path is very time-consuming even on today's most powerful desktop personal computers. Doing so requires finding the path with no such costs, which can be done relatively quickly, and then using the region-specific capital and labour supply equilibrium paths from that simulation as the initial guesses for a run with very small adjustment costs. We then use the results of the small adjustment costs simulation as initial guesses for a simulation with somewhat higher adjustment costs and proceed in this manner until we've solved the model with our desired level of adjustment costs. Given the time required for these calculations, we assumed no adjustment costs in all but one simulation presented below. The simulation with adjustment costs is applied to the baseline transition. The results indicate that inclusion of reasonable adjustment costs makes little difference to the results.
3. Initial Equilibrium and the World Economy's Baseline Transition Path
Table 3 reports key macroeconomic variables in 2004 in the four regions. Note that there is a fairly close accordance between actual and computed values of private consumption and government purchases measured as a share of national income. The one exception is EU government purchases. The official data seem too low given the reported ratio of tax revenues to national income. In our calibration, we chose to benchmark government purchases based on the ratio of tax revenues to national income.
| Model | Official | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| US | EU | Japan | China | US | EU | Japan | China | ||
| National income | |||||||||
| Private consumption | 79.7 | 65.1 | 70.5 | 52.4 | 79.3 | 67.3 | 69.3 | 49.5 | |
| Government purchases of goods and services | 18.7 | 31.0 | 21.9 | 17.9 | 17.4 | 24.3 | 21.7 | 17.6 | |
| General public expenditures | 10.9 | 19.3 | 12.3 | 13.8 | – | – | – | – | |
| Aggregate education outlays | 5.9 | 6.0 | 4.4 | 2.1 | 5.9 | 6.0 | 4.3 | 2.1 | |
| Aggregate health benefits | 1.9 | 5.7 | 5.2 | 2.0 | 2.5 | 6.2 | 6.8 | 2.0 | |
| Current account | 2.8 | 8.3 | 13.8 | −16.1 | −6.1 | 0.5 | 4.5 | 1.9 | |
| Government indicators | |||||||||
| Social contributions received | 8.1 | 16.4 | 13.9 | 7.7 | 7.9 | 16.6 | 13.4 | – | |
| Aggregate pension benefits | 5.3 | 9.2 | 7.6 | 5.2 | 5.7 | 11.6 | 10.8 | 3.0 | |
| Aggregate health benefits | 1.9 | 5.7 | 5.2 | 2.0 | 2.5 | 6.2 | 6.8 | 2.0 | |
| Aggregate disability benefits | 0.9 | 1.5 | 1.1 | 0.0 | 0.9 | – | – | – | |
| Pension contribution rate (%) | 7.7 | 14.2 | 12.1 | 8.0 | 10.6 | – | 17.3 | 11.0 | |
| Health-care contribution rate (%) | 2.5 | 8.8 | 8.2 | 3.1 | 2.9 | – | 8.5 | 8.0 | |
| Disability-insurance contribution rate (%) | 1.4 | 2.3 | 1.8 | 0.0 | 1.9 | ||||
| Interest payment on public debt (%) | 3.3 | 3.8 | 4.1 | 1.0 | 3.0 | 3.5 | 3.7 | 0.8 | |
| Tax revenues (%) | 20.3 | 30.3 | 21.9 | 15.8 | 20.6 | 31.0 | 19.1 | 14.8 | |
| Direct taxes | 12.2 | 14.9 | 11.5 | 5.3 | 12.5 | 15.1 | 8.9 | 2.8 | |
| Personal income taxes | 9.2 | 10.5 | 7.5 | 5.3 | 9.5 | 10.7 | 4.7 | 0.7 | |
| Wage taxes | 5.7 | 5.9 | 4.9 | 5.3 | – | – | – | – | |
| Capital taxes | 3.5 | 4.6 | 2.6 | 0.0 | – | – | – | – | |
| Corporate income taxes | 3.0 | 4.4 | 4.0 | 0.0 | 3.0 | 4.4 | 4.2 | 2.1 | |
| Indirect taxes | 8.1 | 15.4 | 10.4 | 10.5 | 8.1 | 15.9 | 10.2 | 12.0 | |
| Wage tax rates (%) | |||||||||
| Average | 7.8 | 8.0 | 6.6 | 7.1 | – | – | – | – | |
| Marginal | 14.2 | 13.9 | 11.9 | 8.9 | – | – | – | – | |
| Capital-output ratio | 2.2 | 2.2 | 2.3 | 2.6 | – | – | – | – | |
| Capital-labour ratio | 3.0 | 2.9 | 3.1 | 0.5 | – | – | – | – | |
| Interest rate (%) | 9.8 | 9.8 | 9.8 | 9.8 | – | – | – | – | |
|
(a) As a per cent of national income if not stated differently Sources: for official data – European Commission (2005) for the US, EU and Japan; OECD (2002) for China |
|||||||||
The reported ratios of educational expenditure to national income are very close to actual levels.[4] In the case of pension, health and disability expenditures, we closely match the shares of national income received in the form of social contributions in the US, the EU and Japan as reported by the European Commission (2005). In China, the level of health expenditures measured as a share of national income was set in accord with the World Health Organisation (WHO 2004, p 136). The resulting social security payroll tax rates come close to observed levels. Concerning the overall structure of tax revenues, the assumed tax rates on capital income, corporate income and consumption, as well as the expensing fractions (see Table 2) yield a realistic pattern.[5]
The baseline simulation ignores adjustment costs. Hence, capital prices do not change during the transition. However, due to the differences in the expensing fractions for the corporate tax, capital prices deviate from 1 in the EU and Japan. Thus the capital price is 0.964 in the EU and 0.936 in Japan throughout the transition, while it is 1.000 in the US and China. Finally, the model's year-2004 capital-output ratios seem reasonable not only relative to US Commerce Department figures, but also in terms of the year-2004 marginal product of capital, which equals 9.8 per cent.
Next we turn to the simulation results for the baseline transition. The transition paths for the four regions are reported in the first panels of Appendix Tables A1 to A4 (see Appendix A) for the US, the EU, Japan and China. Note that region-specific indices of national income, the capital stock, the supply of labour and the pre-tax wage rate are all expressed relative to the US values in the year 2004.
Although the four economies are ageing, the baseline path shows a steady increase in the effective labour supply in the US, the EU and Japan. This may seem surprising especially for Japan and the EU where the population and workforce decline over time (see Table 1). The explanation lies in our assumption that each successive cohort has a higher effective time endowment, which admits greater effective labour supply by each successive cohort. Thus, the future decrease in the actual labour force is offset in the EU, Japan and China, and the growth in the actual number of workers in the US is augmented. However, effective labour supply grows at much different rates in the regions. In Japan it increases over the century by 41 per cent. In the EU it more than doubles over the same period. And in the US it increases over the century by a factor of almost four.
The evolution of effective labour supply in China is particularly interesting. During the next two decades the effective labour supply increases, then it declines until mid century when it begins to increase again. This complex pattern reflects major changes in substitution and income effects over the transition, the demographic changes themselves, as well as the ongoing technological change. By the end of the century, China's effective labour supply is larger than it is today, but only by 18 per cent.
Due to the dramatic ageing of populations, social security tax rates increase through 2050 by 5.5 percentage points in the US, by 12.8 percentage points in the EU, by 13.8 percentage points in Japan and by 7.8 percentage points in China. Over the century the respective increases are 11.4 percentage points in the US and the EU, 10.7 percentage points in Japan and 16.6 percentage points in China. These changes constitute major payroll tax hikes given the base-year values. In the US and China, for example, the model is predicting an increase in payroll tax rates of more than 100 per cent.
Despite the rising payroll tax burden, capital stocks increase dramatically in all regions over the course of the century. The capital stock increases by a factor of 4.7 in the US, 2.5 in the EU, 1.7 in Japan and 9.6 in China. In China this development is due to high investment rates associated with high private saving and the assumed rapid catch-up in the country's level of technology. The other regions also benefit from the economic boom in China. As the development of the current accounts suggests, initially capital mainly flows from the three developed regions to China. However, in subsequent decades the asset holdings in China of the US, the EU and Japan decline and capital starts to flow from China to all three of these regions. After 2050, this is reversed again so that capital flows from the US, the EU and Japan back to China. This reversal is expected; it reflects the repatriation of Chinese foreign capital earnings back to China.
The differences across the four regions in the growth of the effective labour supply and the capital stock and, in the case of China, in the evolution of the multifactor productivity coefficient materially affect overall economic growth. In the US output grows by a factor of 4.1 over the next 100 years. It grows by a factor of 2.2 in the EU, 1.4 in Japan and 8.5 in China. The larger increase in capital compared to the labour supply leads to an increase in the pre-tax wage rate in the developed economies of almost 16 per cent through the middle of the century. In China wages rise by more than 700 per cent thanks, primarily, to the gradual increase in China's technology level. After 2050, however, growth in the labour supply exceeds growth in capital stocks in all regions so that the wage rate starts to decline. At the end of the century real wages per unit of human capital in the developed economies are still above 2004 levels, but only 4 per cent higher.
As one would expect, the worldwide capital deepening in the first half of the century and capital shallowing in the second half has a major impact on the world interest rate. Between 2004 and 2030 the world interest rate declines by 370 basis points – from 9.8 to 6.1 per cent. This is followed by an increase to a 2100 level of 8.7 per cent. Wage tax rates follow a somewhat similar pattern – declining in the first half of the century and rising in the second half.
This interesting pattern in the evolution of factor prices reflects China's ongoing rapid growth and its assumed gradual change in saving behaviour. During the first half of the century, China makes a major contribution to worldwide capital formation. In the second half of the century, more and more of its cohorts have adopted US preferences with respect to spending and the Chinese saving engine starts to sputter and fail.
To understand better the role of China in worldwide capital formation, let's consider what would happen were the developed world forced to evolve without the ability to import capital from China.
4. The World Economy's Baseline Transition Path Excluding China
Table 4 reports baseline transition paths for the developed economies if we calibrate the model as above, but simply exclude China. Doing so has dramatic effects. Capital stocks in all three regions in the initial years of the transition are much higher compared to the four-country case since more capital now remains in the developed world. For example, in 2010 the capital stock index in the US is 1.60 compared with 1.19 in the four-region simulation (see Table 4). In both simulations, the capital stock is measured relative to the US value in 2004 in the four-country simulation.
| Year | Index of national income | Index of capital stock | Index of labour supply | Current account/ national income |
Index of pre-tax wage | Interest rate | Social security payroll tax rate | Average wage tax | |
|---|---|---|---|---|---|---|---|---|---|
| us | 2004 | 1.01 | 1.37 | 1.01 | −0.057 | 1.00 | 0.072 | 0.114 | 0.076 |
| 2010 | 1.16 | 1.60 | 1.17 | −0.050 | 1.00 | 0.072 | 0.116 | 0.078 | |
| 2020 | 1.45 | 2.04 | 1.43 | −0.039 | 1.01 | 0.070 | 0.141 | 0.080 | |
| 2030 | 1.70 | 2.45 | 1.68 | −0.041 | 1.02 | 0.069 | 0.183 | 0.084 | |
| 2050 | 2.30 | 3.00 | 2.34 | 0.008 | 0.99 | 0.075 | 0.193 | 0.090 | |
| 2075 | 3.07 | 3.71 | 3.20 | 0.010 | 0.96 | 0.081 | 0.214 | 0.082 | |
| 2100 | 3.97 | 4.78 | 4.16 | −0.001 | 0.96 | 0.082 | 0.231 | 0.077 | |
| EU | 2004 | 1.45 | 1.90 | 1.47 | 0.014 | 0.99 | 0.072 | 0.250 | 0.083 |
| 2010 | 1.57 | 2.08 | 1.59 | 0.014 | 0.99 | 0.072 | 0.259 | 0.077 | |
| 2020 | 1.75 | 2.40 | 1.76 | 0.023 | 1.00 | 0.070 | 0.296 | 0.067 | |
| 2030 | 1.83 | 2.55 | 1.83 | 0.025 | 1.01 | 0.069 | 0.365 | 0.056 | |
| 2050 | 1.99 | 2.52 | 2.05 | −0.013 | 0.98 | 0.075 | 0.428 | 0.056 | |
| 2075 | 2.40 | 2.81 | 2.53 | −0.012 | 0.95 | 0.081 | 0.398 | 0.082 | |
| 2100 | 3.08 | 3.59 | 3.26 | 0.000 | 0.95 | 0.082 | 0.374 | 0.093 | |
| Japan | 2004 | 0.50 | 0.68 | 0.50 | 0.077 | 1.01 | 0.072 | 0.216 | 0.061 |
| 2010 | 0.51 | 0.71 | 0.51 | 0.072 | 1.01 | 0.072 | 0.250 | 0.049 | |
| 2020 | 0.53 | 0.75 | 0.52 | 0.030 | 1.02 | 0.070 | 0.307 | 0.034 | |
| 2030 | 0.55 | 0.79 | 0.54 | 0.044 | 1.02 | 0.069 | 0.335 | 0.026 | |
| 2050 | 0.52 | 0.70 | 0.53 | 0.014 | 0.99 | 0.075 | 0.410 | 0.010 | |
| 2075 | 0.57 | 0.71 | 0.59 | −0.004 | 0.97 | 0.081 | 0.375 | 0.028 | |
| 2100 | 0.70 | 0.85 | 0.72 | 0.008 | 0.97 | 0.082 | 0.339 | 0.041 |
Interestingly, even though the developed world has more capital to work with initially, real wages are actually lower in 2010 than in the transition with China. The reason is that the labour supply is initially also much higher in the developed world in the no-China simulation. Presumably this reflects the income effect of having lower real wages in the medium term when China is no longer serving as the developed world's saving machine.
With China out of the picture, capital stocks in the developed regions increase much less rapidly over time. This puts a significant damper on output growth. During the first 25 years of the simulation, capital growth is somewhat larger than labour supply growth. Thus wage rates increase by approximately 2 per cent and the world interest rate decreases by about 30 basis points. In the second half of the century, however, all three regions experience a capital shortage due to the high tax burden. As a consequence, wage rates decline. Indeed, the 2100 wage per unit of human capital is 4 per cent below its 2004 level, and the interest rate is 100 basis points above its base-year value. The lower level of real wages in the no-China transition leads to higher average wage and payroll tax rates, both of which limit capital accumulation.
The current accounts show that capital flows primarily to the US during the coming decades due to its younger population and higher population growth rate. After 2050, capital flows to the EU and increasingly to Japan as the Europeans and Japanese repatriate their US-earned income.
As indicated in the introduction, the no-China developed world transition path shows a relatively modest capital shortage compared to our previous findings reported in Fehr et al (2004a, 2004b, 2005). The main reason, again, is that we are now calibrating the model to include government investment. In addition, we've switched to using European Commission (2005) data for our measures of social contributions received. This lowers, somewhat, initial payroll tax rates as well as subsequent payroll tax hikes.
5. Adjustment Costs
Table 5 repeats the baseline simulation, but includes capital adjustment costs. A comparison of this table with the first panels in Appendix Tables A1–A4 shows that adjustment costs make very little difference to the four-region dynamic equilibrium. The initial levels and time paths of regional stock prices per unit of physical capital (the ratio of the market value to the replacement cost) are, however, interesting.
| Year | Index of national income | Index of capital stock | Index of labour supply | Current account/ national income |
Index of pre-tax wage | Capital price | Interest rate | Social security payroll tax rate | Average wage tax | |
|---|---|---|---|---|---|---|---|---|---|---|
| us | 2004 | 1.02 | 1.00 | 1.02 | −0.015 | 1.00 | 1.000 | 0.098 | 0.114 | 0.083 |
| 2010 | 1.16 | 1.22 | 1.13 | −0.072 | 1.02 | 1.038 | 0.088 | 0.116 | 0.075 | |
| 2020 | 1.46 | 1.87 | 1.38 | −0.145 | 1.08 | 1.062 | 0.068 | 0.136 | 0.073 | |
| 2030 | 1.86 | 2.74 | 1.65 | −0.114 | 1.14 | 1.017 | 0.054 | 0.166 | 0.081 | |
| 2050 | 2.61 | 3.72 | 2.32 | 0.040 | 1.13 | 0.907 | 0.066 | 0.173 | 0.094 | |
| 2075 | 3.26 | 3.88 | 3.07 | 0.039 | 1.07 | 0.902 | 0.084 | 0.208 | 0.077 | |
| 2100 | 4.09 | 4.53 | 3.95 | 0.017 | 1.04 | 0.917 | 0.087 | 0.230 | 0.064 | |
| EU | 2004 | 1.48 | 1.38 | 1.53 | 0.034 | 0.98 | 0.949 | 0.098 | 0.244 | 0.104 |
| 2010 | 1.61 | 1.64 | 1.61 | 0.005 | 1.01 | 0.970 | 0.088 | 0.253 | 0.084 | |
| 2020 | 1.85 | 2.28 | 1.74 | −0.042 | 1.08 | 0.979 | 0.068 | 0.258 | 0.069 | |
| 2030 | 2.05 | 3.00 | 1.82 | −0.036 | 1.14 | 0.933 | 0.054 | 0.326 | 0.069 | |
| 2050 | 2.30 | 3.33 | 2.02 | 0.033 | 1.14 | 0.843 | 0.066 | 0.378 | 0.072 | |
| 2075 | 2.55 | 3.01 | 2.41 | 0.027 | 1.06 | 0.858 | 0.084 | 0.382 | 0.062 | |
| 2100 | 3.15 | 3.39 | 3.07 | 0.023 | 1.03 | 0.882 | 0.087 | 0.370 | 0.062 | |
| Japan | 2004 | 0.47 | 0.50 | 0.46 | 0.100 | 1.02 | 0.874 | 0.098 | 0.229 | 0.049 |
| 2010 | 0.49 | 0.55 | 0.47 | 0.046 | 1.05 | 0.909 | 0.088 | 0.261 | 0.030 | |
| 2020 | 0.53 | 0.72 | 0.49 | −0.069 | 1.11 | 0.938 | 0.068 | 0.303 | 0.021 | |
| 2030 | 0.60 | 0.91 | 0.52 | −0.057 | 1.16 | 0.901 | 0.054 | 0.308 | 0.032 | |
| 2050 | 0.61 | 0.95 | 0.52 | 0.045 | 1.17 | 0.804 | 0.066 | 0.356 | 0.035 | |
| 2075 | 0.61 | 0.78 | 0.56 | 0.036 | 1.09 | 0.818 | 0.084 | 0.352 | 0.031 | |
| 2100 | 0.71 | 0.82 | 0.68 | 0.026 | 1.05 | 0.851 | 0.087 | 0.329 | 0.030 | |
| China | 2004 | 1.24 | 1.52 | 8.57 | −0.066 | 0.15 | 1.161 | 0.098 | 0.110 | 0.052 |
| 2010 | 2.04 | 2.32 | 9.45 | 0.025 | 0.23 | 1.235 | 0.088 | 0.085 | 0.074 | |
| 2020 | 3.78 | 4.81 | 9.95 | 0.086 | 0.39 | 1.196 | 0.068 | 0.088 | 0.068 | |
| 2030 | 5.42 | 8.25 | 9.05 | 0.059 | 0.61 | 1.080 | 0.054 | 0.117 | 0.045 | |
| 2050 | 8.36 | 12.84 | 8.06 | −0.025 | 1.04 | 0.937 | 0.066 | 0.187 | 0.004 | |
| 2075 | 9.66 | 13.32 | 8.69 | −0.023 | 1.12 | 0.885 | 0.084 | 0.264 | 0.018 | |
| 2100 | 11.37 | 14.48 | 10.51 | −0.014 | 1.09 | 0.914 | 0.087 | 0.277 | 0.036 |
In 2004, EU stock prices are 5.1 per cent lower than US stock prices. Japanese stock prices are 12.6 per cent lower, and Chinese stock prices are 16.1 per cent higher. The model predicts increases in stock values in all four regions for the next 10 to 20 years, depending on the region, followed by a long-term decline in stock values. The US stock market value is 1.000 in 2004, hits 1.062 in 2020, and falls to 0.917 in 2100. The EU's 2004 stock market value is 0.949. It is 0.979 in 2020 and then it gradually falls to 0.882 by 2100. Japan's 2004 stock market value is 0.874. In 2020 it is 0.938, but it falls to 0.851 by century's end. And China's stock market value starts at 1.161, reaches 1.196 in 2020 and declines to 0.914 by 2100.
6. Examining China's Saving and Absorption of Technology
This section returns to the four-region model without adjustment costs and examines the importance of our assumptions about the evolution of Chinese saving behaviour and the rate at which China absorbs developed-world technology. Specifically, we first consider keeping the time preference rate of successive Chinese cohorts at the same level that was calibrated for all Chinese cohorts for 2004 in the baseline transition. Next we assume the technology coefficient in the Chinese Cobb-Douglas production function rises only to 50 per cent of the US level (rather than 100 per cent) by 2050 and remains at that value thereafter.
6.1 Constant time preference rate in China
The second simulation reported in Appendix Tables A1–A4 permanently maintains the Chinese time preference rate at its year-2004 level. Doing so has dramatic consequences. In particular, the 2100 world stock of capital is 5.9 times higher than in the base case! China not only becomes the world's saver, it also becomes the world's investor, sending huge flows of capital to the developed world over the course of the century. By 2100, the capital stocks in the US, the EU and Japan are 5.6, 5.6 and 5.8 times their initial values, respectively.
This huge impetus to capital formation has a major impact on economic growth in all four regions, leaving world output roughly 50 per cent higher in 2100 than it would otherwise have been. This is true notwithstanding a basically unchanged supply of labour in the four regions. The rough constancy of the labour supply reflects competing income and substitution effects arising from the level of the real wage per unit of human capital being roughly 55 per cent higher in the long run (year 2100). The long-run capital glut also leads to a major decline in the world real interest rates – from 9.8 per cent in 2004 to 2.3 per cent in 2100.
The long-run increase in real wages has a major effect on long-run payroll tax rates, although it does little to payroll tax rates over the next three decades. Year-2100 payroll tax rates are now 16.4 per cent instead of 23.0 per cent in the US, 26.1 per cent instead of 36.7 per cent in the EU, 22.7 per cent instead of 32.8 per cent in Japan and 26.0 per cent instead of 27.7 per cent in China. Higher output growth immediately translates into increased government expenditures. This explains the higher wage tax rates in the medium and long run.
6.2 Slower technology growth in China
Our next simulation, reported in the third panels of Appendix Tables A1–A4, assumes that the multifactor technology coefficient in the Chinese production function rises to only 50 by 2050, rather than 100 per cent of the US level and remains fixed at half the US level thereafter. As a comparison with the base case shows, slower Chinese technological growth means much lower capital demand, output and real wage levels in China. Indeed, in 2100 the Chinese capital stock and output levels are just over half of their baseline values. And the Chinese real wage is only 39 per cent of what it would otherwise have been.
In contrast to what happens to China's capital stock, China's labour supply is significantly higher along the entire transition path. This reflects the income effects (relative to the base case) experienced by the Chinese who receive lower real wages as well as smaller inheritances. These income effects matter to the labour supply from the get go. Indeed, the immediate increase in labour supply explains why Chinese output and capital stock levels are initially higher than they are in the base case.
The rise in China's labour supply doesn't suffice to offset the lower path of wages with respect to determining the Chinese payroll tax base. Consequently, social security payroll tax rates are markedly higher during this transition.
The most interesting thing about this simulation of slower Chinese technological progress is what happens to the economies of the developed world. The answer, surprisingly, is very little. Although China saves much less than in the base case, it also demands significantly less capital. Consequently, the US, the EU and Japan end up with essentially the same capital stocks, wage rates and tax rates over time that they enjoy in the base case.
The welfare effects of this simulation are given in Table 6. The numbers show the change in welfare measured as an equivalent variation and expressed as a percentage of remaining lifetime resources for cohorts born between 1920 and 2030. As expected from the macroeconomic development, middle-aged and future cohorts in China experience large welfare losses due to reduced wages and increased payroll tax rates during their lifetimes. The welfare changes for developed-world cohorts are, in contrast, quite small.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −0.73 | −0.49 | −0.10 | −0.68 | −0.48 | −0.15 | |
| 1930 | −1.58 | −1.18 | −0.38 | −1.25 | −1.08 | −0.63 | |
| 1940 | −2.34 | −1.88 | −0.72 | −2.01 | −1.74 | −1.02 | |
| 1950 | −1.53 | −1.43 | −1.02 | −1.98 | −1.76 | −1.15 | |
| 1960 | −0.10 | −0.66 | −0.98 | −0.21 | −0.79 | −1.10 | |
| 1970 | 1.61 | 0.54 | −0.50 | 0.97 | 0.06 | −0.86 | |
| 1980 | 2.35 | 1.32 | 0.10 | 1.12 | 0.33 | −0.65 | |
| 1990 | 2.16 | 1.35 | 0.33 | 1.38 | 0.80 | −0.22 | |
| 2000 | 1.38 | 0.90 | 0.28 | 0.71 | 0.39 | −0.20 | |
| 2010 | 0.57 | 0.38 | 0.14 | −0.03 | −0.09 | −0.20 | |
| 2020 | 0.05 | 0.07 | 0.07 | −0.46 | −0.35 | −0.14 | |
| 2030 | −0.40 | −0.21 | 0.00 | −0.74 | −0.52 | −0.09 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −0.70 | −0.40 | −0.11 | 1.06 | 2.24 | 2.06 | |
| 1930 | −1.57 | −1.16 | −0.55 | 0.22 | 1.33 | 1.31 | |
| 1940 | −2.40 | −1.94 | −1.12 | −1.06 | 0.10 | 0.40 | |
| 1950 | −2.25 | −1.98 | −1.35 | −10.08 | −8.07 | −4.25 | |
| 1960 | −0.26 | −0.85 | −1.11 | −21.70 | −17.12 | −7.99 | |
| 1970 | 1.22 | 0.24 | −0.75 | −28.60 | −22.17 | −9.05 | |
| 1980 | 1.55 | 0.68 | −0.39 | −33.45 | −24.66 | −7.85 | |
| 1990 | 2.10 | 1.35 | 0.17 | −40.40 | −30.67 | −12.50 | |
| 2000 | 1.46 | 0.99 | 0.18 | −45.17 | −35.54 | −18.92 | |
| 2010 | 0.66 | 0.48 | 0.10 | −48.43 | −38.65 | −22.54 | |
| 2020 | 0.12 | 0.14 | 0.08 | −51.18 | −41.00 | −24.34 | |
| 2030 | −0.33 | −0.16 | 0.09 | −53.03 | −42.83 | −25.89 | |
7. Population Scenarios
In this section we analyse three different population scenarios. The first scenario keeps fertility rates fixed at their initial levels. The second scenario considers increases in life expectancy relative to the base case. The third scenario doubles rates of immigration in all four regions.[6]
7.1 Fixed fertility rates in all regions
The fourth panels in Appendix Tables A1–A4 show the impact of keeping the initial fertility rate of 2.11 births per woman in the US, 1.46 births in the EU, 1.28 births in Japan and 1.62 births in China fixed through to 2050.[7]
The higher short-term US fertility rate increases that country's total population as well as its effective labour supply. The latter variable is first affected in 2026 when the first cohort generated by the higher birth rate enters the labour force. The effective labour supply and national income in 2100 are raised by 17 per cent relative to the baseline simulation. Due to the younger population age-structure and the increased labour supply, social security contribution rates in the US decrease. In 2100 the social security payroll tax is 20.9 per cent, compared to 23 per cent in the base case. However, the average wage tax rate rises. Compared with the baseline results, the average wage tax rate is 1.1 percentage points higher in 2100. This reflects the need to finance additional government expenditures associated with the population increase. The capital stock keeps pretty close track with the higher time path of labour supply. In 2100 the capital stock is 16 per cent higher relative to the base case.
In the case of the EU, Japan and China, holding fertility rates fixed at their 2004 values for the next 45 years leads to smaller workforces and populations. In the EU, the labour supply and national income in 2100 are 23 per cent below their baseline values. These are big differences. In China, effective labour supply and national income in 2100 are both 17 per cent lower. And in Japan, the maintenance of current fertility patterns through 2050 reduces effective labour supply at the end of the century by 33 per cent and national income by 32 per cent. Indeed, the absolute size of the Japanese economy, as measured by national income, is smaller in 2100 than in 2004 notwithstanding almost 100 years of technological progress!
Lower fertility rates raise dependency ratios in the three developed regions. This necessitates larger increases in social security tax rates. On the other hand, average wage tax rates are slightly reduced during the transition, since government expenditures on education decrease with the reduction in the number of young people and general government expenditures decrease with the reduction in population growth. The higher payroll taxes in China, Japan and the EU lead households to save less and export more capital to the US. Thus, capital stocks in the three regions decline during the second half of the century. Finally, since capital-labour ratios are little affected in the four regions, wage rates and the world interest rate remain almost the same as in the baseline path.
7.2 Higher life expectancies in all regions
Now we consider a simultaneous rise in longevity in all regions. To be precise, we gradually raise life expectancy in each region through 2050 by approximately 3 years, that is life expectancy in 2050 is 86.8 years in the US, 87.6 years in the EU, 91 years in Japan, and 83.3 years in China. These values for the developed regions find support in the projections of Tuljapurkar, Li and Boe (2000). Simulation results for this scenario are reported in the fifth panels of Appendix Tables A1–A4.
Greater longevity leads to more saving for retirement as well as more labour supply to help generate this saving. Consequently, the labour supply and the capital stock increase in all four regions compared to the base case. The broadening of the tax base implies a slight decline in wage tax rates in the medium and long run. However, at the same time, higher life expectancy leads to a rise in dependency ratios. Hence, the year-2100 social security contribution rates are increased relative to the base case by 2.4 percentage points in the US, 2.3 percentage points in the EU, 2.2 percentage points in Japan, and 4.1 percentage points in China. Since the increase in capital exceeds the increase in labour, wage rates rise slightly during the transition. Consequently, the values of the world interest rate are lower than in the baseline path.
7.3 Doubling of immigration in all regions
The sixth panels in Appendix Tables A1–A4 show the impact of doubling immigration immediately and permanently in all four regions. This means, for example, that in 2004, 2 million immigrants enter the US, 900,000 enter the EU, 108,000 enter Japan and 780,000 exit China.
As is clear from the figures for the effective labour supply, doubling immigration makes a material difference to the long-run supply of labour in all four regions. Take the developed regions. Relative to the baseline simulation, this policy raises the effective labour supply in 2100 by 31 per cent in the US, 21 per cent in the EU, and 10 per cent in Japan. The remarkable thing is how long it takes for immigration to alter effective labour supplies. In the US, for example, the effective supply of labour is only 11 per cent larger in 2030 despite a doubling of immigration starting in 2004. The comparable figures for the EU and Japan are 6 per cent and 2 per cent.
Given that the developed world's severe fiscal problems associated with ageing will begin to appear well before 2030, it would seem that even a doubling of immigration is ‘too little too late’. This, indeed, is what the other figures in the second panel of results show. Relative to the baseline simulation, doubling immigration makes little difference to any of the three countries in terms of their macroeconomic variables.
Take the US. With a doubling of immigration, the payroll tax rate is 15.3 per cent in 2030 – not much lower than the 16.4 per cent rate without the extra immigrants. In 2100 the payroll tax rate is 22.4 per cent, compared with 23.0 per cent under the baseline immigration policy. Factor prices are also essentially unchanged by a doubling of immigration. In 2030, the pre-tax wage is 1.17 in both simulations. And in 2100, the pre-tax wage is 1.05 compared to 1.04 in the base case. The explanation here is that, while the long-run US labour supply rises by 31 per cent, the long-run capital stock rises by 33 per cent, leaving the long-run capital-labour ratio essentially unchanged.
If the long-run real wage in the US stays fixed, but labour supply rises by 31 per cent, why doesn't the payroll tax rate and, for that matter, the average wage tax rate fall by 31 per cent in light of the 31 per cent larger long-run supply of effective labour? The answer is that the model provides new immigrants with public goods and social insurance benefits on the same basis as existing natives. And doubling the number of immigrants on an across-the-board basis ends up costing the US government almost as much in additional expenditures as the US government earns in additional revenues. As Appendix Tables A2 and A3 indicate, the same can be said of the EU and Japan.
Of course, the opposite happens in China. Higher emigration reduces China's long-run labour supply by 5 per cent and long-run capital stock by 3 per cent. More emigrants mean a reduction in the taxable wage base and thus an increase in payroll tax rates. However, as the results indicate, the changes in payroll tax rates are quite small.
Table 7 reports the welfare effects of doubling immigration. Almost all cohorts in the developed regions experience welfare gains, albeit mostly very small ones. For initially younger and future generations these gains stem from the reduction in payroll taxes. The gains are smaller for members of the high-income class because the ceiling on key payroll taxes limits the benefits they can experience from cuts in these taxes. Welfare gains are generally higher in the US and the EU. This is particularly true of younger and future cohorts. Indeed, for the low-income cohort born in 2030, the welfare gain is 2.07 per cent in the EU and 1.35 per cent in the US, but only 1.03 per cent in Japan. Unlike the gains of initial older generations, these gains are substantial. They appear to reflect the reduction in excess burden arising from even the modest reductions in marginal tax rates arising from the immigration reform.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1930 | 0.03 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | |
| 1940 | 0.06 | 0.05 | 0.03 | 0.06 | 0.05 | 0.04 | |
| 1950 | 0.13 | 0.09 | 0.04 | 0.10 | 0.08 | 0.05 | |
| 1960 | 0.07 | 0.06 | 0.04 | 0.04 | 0.06 | 0.05 | |
| 1970 | −0.03 | 0.01 | 0.01 | 0.02 | 0.06 | 0.05 | |
| 1980 | 0.69 | 0.50 | 0.23 | 0.21 | 0.19 | 0.07 | |
| 1990 | 0.64 | 0.47 | 0.19 | 0.41 | 0.34 | 0.02 | |
| 2000 | 0.89 | 0.67 | 0.30 | 0.79 | 0.65 | 0.03 | |
| 2010 | 1.04 | 0.78 | 0.37 | 1.28 | 1.05 | 0.10 | |
| 2020 | 1.12 | 0.83 | 0.39 | 1.70 | 1.40 | 0.20 | |
| 2030 | 1.35 | 0.98 | 0.44 | 2.07 | 1.68 | 0.30 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | 0.01 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1930 | 0.04 | 0.03 | 0.02 | 0.02 | 0.02 | 0.02 | |
| 1940 | 0.08 | 0.07 | 0.05 | 0.08 | 0.08 | 0.06 | |
| 1950 | 0.11 | 0.10 | 0.07 | 0.21 | 0.18 | 0.11 | |
| 1960 | 0.05 | 0.07 | 0.06 | 0.22 | 0.18 | 0.11 | |
| 1970 | 0.00 | 0.04 | 0.05 | 0.11 | 0.12 | 0.09 | |
| 1980 | 0.03 | 0.06 | 0.05 | −0.05 | 0.04 | 0.06 | |
| 1990 | 0.05 | 0.07 | 0.01 | −0.20 | −0.06 | 0.05 | |
| 2000 | 0.18 | 0.17 | −0.01 | −0.29 | −0.14 | 0.03 | |
| 2010 | 0.39 | 0.32 | 0.00 | −0.25 | −0.12 | 0.04 | |
| 2020 | 0.68 | 0.53 | 0.04 | −0.18 | −0.09 | 0.01 | |
| 2030 | 1.03 | 0.79 | 0.10 | −0.21 | −0.14 | −0.03 | |
Initially middle-aged people in China experience small welfare gains which are mainly due to small reductions in the average wage tax. In contrast, younger and future cohorts experience welfare losses. Of course, the reason is the higher payroll tax rates throughout the transition. As one would expect from the macroeconomic outcomes, welfare effects in China are much smaller than in the developed regions.
8. Social Security Policies
This section considers different social insurance policy scenarios. The first is a larger increase in health expenditures than that assumed in the base case. The second and third scenarios analyse the consequences of different financing methods for the social security systems. The fourth scenario considers cuts in state pension systems. The final scenario is a privatisation of public pension systems.
8.1 Increased health expenditures
In this simulation, health expenditures increase by 3 per cent during the first 25 years of the transition instead of the 2 per cent rate assumed in the base case. The simulation results are shown in the seventh panels of Appendix Tables A1–A4.
Higher health expenditures increase social security contributions. The additional increases in payroll taxes depend on the relative sizes of overall health expenditures and populations in each region. Thus in 2030, payroll tax rates are above their baseline values by 1.3 percentage points in the US, 3.2 percentage points in the EU, and 3.5 percentage points in Japan and China. In the year 2100 the difference is 1.8 percentage points in the US, 3.2 percentage points in the EU, 3.7 percentage points in Japan, and 0.8 percentage points in China.
The higher payroll tax burden leads to lower net wages. Consequently, medium-term and long-run capital stocks are below their respective baseline values. Lower capital formation is partly offset by higher capital inflows into the three developed regions from China during the first decades of the century. This explains the slightly increased output growth during this period. In the long run, output in the US and China is lower compared to the base case and higher in the EU and Japan. This is due to the adjustment in the effective labour supply in order to offset the income losses. Higher output growth during the first decades and lower wages in the second half of the century lead to an additional increase in wage tax rates.
The welfare effects of this simulation as reported in Table 8 confirm our macroeconomic findings. Apart from small welfare gains for initially older generations in the EU and Japan, all cohorts already alive in the initial year and all future cohorts experience welfare losses from increased health expenditures. The explanation is the higher payroll and wage tax rates. Since the additional tax burden increases with time, welfare losses rise with the birth year of the observed generations. Note also the differences in welfare losses between the four regions. Generations in the EU and Japan are hurt much more than in the US and China. This indicates the bigger size of health expenditures in the former two regions and thus the larger required increase in tax rates.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | 0.00 | 0.01 | 0.00 | 0.07 | 0.08 | −0.01 | |
| 1930 | −0.03 | −0.01 | −0.01 | 0.05 | 0.07 | −0.02 | |
| 1940 | −0.05 | −0.03 | −0.02 | 0.03 | 0.04 | −0.03 | |
| 1950 | −0.06 | −0.04 | −0.02 | −0.06 | −0.03 | −0.04 | |
| 1960 | −0.08 | −0.06 | −0.03 | −0.29 | −0.19 | −0.08 | |
| 1970 | −0.18 | −0.13 | −0.06 | −0.69 | −0.50 | −0.14 | |
| 1980 | −0.35 | −0.25 | −0.13 | −1.17 | −0.88 | −0.23 | |
| 1990 | −0.67 | −0.49 | −0.26 | −2.17 | −1.73 | −0.45 | |
| 2000 | −1.08 | −0.79 | −0.44 | −3.29 | −2.68 | −0.71 | |
| 2010 | −1.35 | −0.98 | −0.54 | −4.05 | −3.36 | −0.91 | |
| 2020 | −1.50 | −1.08 | −0.58 | −4.54 | −3.81 | −1.04 | |
| 2030 | −1.68 | −1.22 | −0.64 | −4.91 | −4.15 | −1.15 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | 0.07 | 0.04 | −0.02 | −0.02 | −0.01 | −0.01 | |
| 1930 | 0.04 | 0.02 | −0.03 | −0.04 | −0.03 | −0.03 | |
| 1940 | 0.02 | 0.00 | −0.05 | −0.08 | −0.07 | −0.06 | |
| 1950 | −0.07 | −0.05 | −0.05 | −0.17 | −0.14 | −0.08 | |
| 1960 | −0.33 | −0.22 | −0.08 | −0.19 | −0.15 | −0.05 | |
| 1970 | −0.77 | −0.55 | −0.13 | −0.26 | −0.19 | −0.04 | |
| 1980 | −1.26 | −0.92 | −0.19 | −0.42 | −0.25 | −0.02 | |
| 1990 | −2.32 | −1.79 | −0.35 | −0.78 | −0.48 | −0.07 | |
| 2000 | −3.49 | −2.72 | −0.56 | −1.29 | −0.88 | −0.29 | |
| 2010 | −4.20 | −3.29 | −0.71 | −1.72 | −1.22 | −0.53 | |
| 2020 | −4.77 | −3.79 | −0.83 | −1.90 | −1.34 | −0.58 | |
| 2030 | −5.23 | −4.20 | −0.93 | −2.02 | −1.42 | −0.61 | |
8.2 Financing social security benefits at the margin with general tax revenues
Next we consider a scenario where payroll tax rates are fixed at their year-2004 values throughout the transition. The budgets of the social security systems are then financed by general tax revenues. The results are reported in the eighth panels of Appendix Tables A1–A4.
Balancing the future budgets of the social security systems by general tax revenues increases the wage tax rate in all four regions. In year 2100, the average wage tax rate is now 17.8 per cent in the US instead of 6.8 per cent in the base case. In the EU it is 17.8 per cent instead of 7.4 per cent, in Japan 12.0 per cent instead of 2.7 per cent, and in China 17.6 per cent instead of 1.9 per cent. Note that the wage tax rates do not increase as much as the payroll tax rates would otherwise have risen because there is no ceiling on wages subject to taxation. This differentially reduces the welfare of high-earning agents. It also reduces their ability to save and their desire to work. Thus capital stocks, labour supply and national income are lower than in the base case. The paths of current accounts, wage rates and interest rates are, however, little changed.
Table 9 records the welfare effects of this policy. Agents in the low- and middle-income classes experience welfare gains since they now face a lower tax burden. Note also the differences in welfare effects between the developed regions, which stem from the different extents of population ageing in the three regions. At first glance it might be surprising that initially middle-aged and younger cohorts in the low- and middle-income classes in China experience small welfare losses while those in the high-income class enjoy welfare gains. The reason is that payroll taxes in China decline in the baseline transition during the first few decades. Keeping payroll tax rates fixed at the year-2004 level translates into lower average net wages during these decades than would otherwise be the case. This, of course, hurts people in the low- and middle-income classes, while those in the high-income class end up better off. High-income workers are less affected by the maintenance of existing payroll tax rates due to the payroll tax ceiling gain.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −0.02 | −0.01 | 0.00 | −0.05 | −0.03 | −0.04 | |
| 1930 | −0.02 | −0.01 | 0.00 | −0.05 | −0.04 | −0.05 | |
| 1940 | −0.04 | −0.02 | −0.01 | −0.06 | −0.05 | −0.04 | |
| 1950 | −0.02 | −0.02 | −0.01 | −0.02 | −0.02 | −0.02 | |
| 1960 | 0.00 | −0.01 | −0.01 | 0.09 | 0.04 | −0.03 | |
| 1970 | 0.05 | 0.02 | −0.02 | 0.22 | 0.14 | −0.10 | |
| 1980 | 0.12 | 0.07 | −0.08 | 0.39 | 0.27 | −0.20 | |
| 1990 | 0.20 | 0.13 | −0.16 | 0.73 | 0.56 | −0.62 | |
| 2000 | 0.28 | 0.19 | −0.25 | 1.13 | 0.89 | −1.09 | |
| 2010 | 0.33 | 0.23 | −0.28 | 1.48 | 1.21 | −1.53 | |
| 2020 | 0.34 | 0.25 | −0.35 | 1.65 | 1.38 | −1.87 | |
| 2030 | 0.35 | 0.26 | −0.49 | 1.65 | 1.40 | −2.06 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −0.08 | −0.04 | −0.23 | 0.00 | 0.02 | −0.08 | |
| 1930 | −0.08 | −0.04 | −0.19 | 0.00 | 0.01 | −0.08 | |
| 1940 | −0.10 | −0.06 | −0.26 | −0.02 | −0.01 | −0.10 | |
| 1950 | 0.05 | 0.02 | −0.14 | −0.19 | −0.15 | 0.02 | |
| 1960 | 0.37 | 0.23 | −0.12 | −0.34 | −0.27 | 0.11 | |
| 1970 | 0.62 | 0.43 | −0.34 | −0.30 | −0.24 | 0.10 | |
| 1980 | 0.80 | 0.58 | −0.50 | −0.20 | −0.18 | 0.04 | |
| 1990 | 1.19 | 0.91 | −0.94 | −0.02 | −0.07 | −0.03 | |
| 2000 | 1.47 | 1.11 | −1.17 | 0.21 | 0.11 | −0.13 | |
| 2010 | 1.75 | 1.34 | −1.43 | 0.35 | 0.23 | −0.19 | |
| 2020 | 2.05 | 1.62 | −1.82 | 0.38 | 0.26 | −0.30 | |
| 2030 | 2.18 | 1.75 | −2.09 | 0.44 | 0.30 | −0.46 | |
8.3 Financing social security benefits with government debt
This scenario examines the consequences of financing social security benefits through to 2029 with government debt. To be precise, we keep payroll tax rates in each region fixed at their year-2004 values through to 2029. We also fix the intercept and the progressive terms of our wage tax rate formula at their 2004 values. The governments' general budgets and the budgets of the social security systems are then balanced with government debt. Starting in year 2030, payroll tax rates and the intercept of the payroll tax rate formula endogenously adjust to balance social security systems and government general budgets, respectively. In the year 2030 and thereafter we keep government debt fixed as a share of national income. The ninth panels in Appendix Tables A1–A4 report results.
From 2004 to 2100, in the US debt increases from 33.3 to 73.8 per cent of national income, in the EU from 38.9 to 134.6 per cent, and in Japan from 41.4 to 249.5 per cent. In China, payroll tax and wage tax rates decline (with some minor exceptions) in each year during the first few decades of the baseline transition. Consequently, holding these tax rates fixed through 2030 in China means running a budget surplus. Indeed, in 2100 government debt in China is negative 38.8 per cent of national income, rather than positive 10 per cent – its baseline year-2100 value.
Higher debt ultimately implies higher average tax rates in order to finance higher interest payments. In 2100, average wage tax rates are 11.9 per cent in the US, 22.5 per cent in the EU, and 33.1 per cent in Japan. The corresponding 2100 baseline average wage tax rates are 6.8 per cent in the US, 7.4 per cent in the EU and 2.7 per cent in Japan.
These are, obviously, huge increases. Of course, one would expect capital formation, labour supply and output growth to be greatly reduced by this policy. But this doesn't happen because China's budget surplus provides an additional pool of savings for foreign investment.
Next, consider the welfare effects of this policy, shown in Table 10. Initial middle-aged and younger generations in the US, the EU and Japan gain from this policy reform. This reflects, of course, the fact that they enjoy constant rather than rising tax rates through 2030. The gains are largest in Japan since in the baseline path its taxpayers experience the largest increase in social security contributions. Future cohorts in the developed regions experience remarkably large welfare losses. These stem from the large increase in wage taxes to finance the higher government debt. Take, as an example, members of the 2030 Japanese birth cohort. Low-income members of this cohort experience a 20.25 per cent welfare loss. This demonstrates the dramatic increase in excess burdens due to the adjustment in the wage taxes. The opposite is observed in China. Here middle-aged people lose from the reform since they now face higher payroll tax burdens. Future cohorts, however, experience welfare gains from the lower and even negative wage taxes.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | 0.01 | −0.02 | 0.00 | −0.09 | −0.12 | 0.02 | |
| 1930 | 0.09 | 0.05 | 0.02 | −0.04 | −0.07 | 0.06 | |
| 1940 | 0.18 | 0.13 | 0.06 | 0.06 | 0.02 | 0.11 | |
| 1950 | 0.26 | 0.19 | 0.11 | 0.35 | 0.23 | 0.15 | |
| 1960 | 0.43 | 0.31 | 0.17 | 0.83 | 0.60 | 0.27 | |
| 1970 | 0.53 | 0.44 | 0.27 | 1.53 | 1.18 | 0.42 | |
| 1980 | 0.23 | 0.28 | 0.24 | 0.90 | 0.87 | 0.34 | |
| 1990 | −0.07 | 0.10 | 0.18 | 0.06 | 0.32 | 0.07 | |
| 2000 | −1.00 | −0.58 | −0.14 | −2.45 | −1.69 | −0.69 | |
| 2010 | −3.03 | −2.16 | −1.06 | −7.01 | −5.74 | −2.21 | |
| 2020 | −3.55 | −2.52 | −1.22 | −8.56 | −7.11 | −2.85 | |
| 2030 | −4.08 | −2.89 | −1.36 | −10.72 | −9.06 | −3.77 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −0.28 | −0.18 | 0.08 | 0.07 | 0.06 | 0.03 | |
| 1930 | −0.19 | −0.19 | 0.10 | 0.13 | 0.12 | 0.08 | |
| 1940 | −0.10 | −0.02 | 0.19 | 0.29 | 0.28 | 0.20 | |
| 1950 | 0.62 | 0.42 | 0.26 | 0.56 | 0.48 | 0.29 | |
| 1960 | 2.27 | 1.53 | 0.44 | 0.46 | 0.39 | 0.24 | |
| 1970 | 3.50 | 2.59 | 0.62 | 0.21 | 0.24 | 0.20 | |
| 1980 | 1.75 | 1.62 | 0.39 | 0.23 | 0.32 | 0.20 | |
| 1990 | −0.62 | 0.00 | −0.39 | −0.02 | 0.17 | 0.22 | |
| 2000 | −6.90 | −5.10 | −2.30 | −0.53 | −0.22 | 0.09 | |
| 2010 | −15.80 | −12.97 | −5.31 | −1.00 | −0.60 | −0.18 | |
| 2020 | −17.05 | −14.03 | −5.95 | −0.93 | −0.49 | −0.05 | |
| 2030 | −20.25 | −16.94 | −7.42 | −0.75 | −0.30 | 0.16 | |
8.4 Cutting pension-benefit replacement rates
As mentioned, our baseline path includes the legislated cut in the pension replacement rates in Japan of 20 per cent that is being phased in between now and 2017. We now assume the same cut occurs in all other regions over the same period. The simulation results are reported in the tenth panels of Appendix Tables A1–A4. In 2100, social security contribution rates are reduced by 3.6 percentage points in the US, by 4.7 percentage points in the EU and by 4.6 percentage points in China compared to the respective baseline values. As one would expect, this policy increases capital formation in the three regions. Thus the long-run capital stock is increased by 11.6 per cent in the US, by 10.3 per cent in the EU and by 11.2 per cent in China relative to the base case. At the same time, the labour supply is slightly reduced and output growth increases. The higher capital-labour ratios lead to higher wages and lower interest rates during the transition. Due to higher wage income, the average wage tax rates in the three regions are lower than in the baseline path.
The pension reform in the US, the EU and China also affects the Japanese economy in the future. Larger capital stocks in the US, the EU and China lead to larger capital imports by Japan. Consequently, Japan's capital stock and national income are also higher compared to the base case. The increase in wages during the transition lowers payroll tax rates slightly since the labour supply remains unaffected. However, the average wage tax rate increases due to the higher growth in general government expenditures arising from higher output growth.
As the welfare effects in Table 11 indicate, initially middle-aged people lose from this policy reform in all four regions. In the US, the EU and China this reflects the cut in pension replacement rates. People now receive lower benefits than under the baseline scenario. In Japan the losses stem from the increases in the average wage tax rate. Initial older cohorts in the four regions are almost unaffected. Initial young and future cohorts, however, gain in all four regions. The reason is mainly the reduction in payroll and wage tax rates in the US, the EU and China and the increased wages that outweigh the benefit losses. In Japan, the welfare gains of the low- and middle-income classes also stem from the reduction in payroll taxes and the higher wages. The highest income classes are adversely affected by the increase in the wage tax rate.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | 0.21 | 0.12 | 0.00 | 0.34 | 0.23 | −0.04 | |
| 1930 | 0.10 | 0.03 | −0.03 | 0.28 | 0.17 | −0.10 | |
| 1940 | −0.02 | −0.08 | −0.09 | 0.13 | 0.03 | −0.17 | |
| 1950 | −2.84 | −1.59 | −0.48 | −3.04 | −1.75 | −0.48 | |
| 1960 | −1.80 | −1.11 | −0.46 | −2.98 | −1.84 | −0.57 | |
| 1970 | −0.49 | −0.34 | −0.25 | −1.11 | −0.70 | −0.35 | |
| 1980 | 0.67 | 0.46 | 0.08 | 0.41 | 0.35 | −0.10 | |
| 1990 | 1.64 | 1.15 | 0.38 | 2.29 | 1.83 | 0.36 | |
| 2000 | 2.84 | 1.76 | 0.64 | 4.21 | 3.33 | 0.78 | |
| 2010 | 3.04 | 2.13 | 0.79 | 5.76 | 4.57 | 1.11 | |
| 2020 | 3.51 | 2.42 | 0.86 | 6.87 | 5.48 | 1.34 | |
| 2030 | 4.02 | 2.77 | 0.94 | 7.58 | 6.07 | 1.48 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −0.10 | −0.03 | 0.00 | 0.04 | 0.18 | 0.25 | |
| 1930 | −0.20 | −0.12 | −0.05 | −0.05 | 0.08 | 0.16 | |
| 1940 | −0.36 | −0.26 | −0.15 | −0.27 | −0.13 | 0.00 | |
| 1950 | −0.45 | −0.36 | −0.23 | −3.71 | −3.14 | −1.79 | |
| 1960 | −0.23 | −0.27 | −0.25 | −3.18 | −2.55 | −1.32 | |
| 1970 | 0.06 | −0.11 | −0.25 | −1.71 | −1.39 | −0.73 | |
| 1980 | 0.23 | 0.01 | −0.23 | −0.74 | −0.74 | −0.43 | |
| 1990 | 0.60 | 0.28 | −0.13 | 0.50 | 0.07 | −0.29 | |
| 2000 | 0.83 | 0.41 | −0.12 | 2.03 | 1.23 | 0.19 | |
| 2010 | 0.98 | 0.50 | −0.15 | 3.33 | 2.22 | 0.83 | |
| 2020 | 1.16 | 0.62 | −0.20 | 3.84 | 2.53 | 0.93 | |
| 2030 | 1.31 | 0.71 | −0.31 | 4.36 | 2.86 | 1.00 | |
8.5 Privatising pensions
Our final scenario is complete pension privatisation, which we model as the elimination of any new public pension benefit accrual coupled with the establishment of individual accounts. The reform entails paying off all accrued benefits to those retired in 2004 and to those working in 2004 when they reach retirement. To approximate this pay-off of accrued benefits we pay initial retirees their full benefits over time and pay post-2004 retirees benefits in retirement whose values are linearly phased out over a 45-year period starting in 2004. Thus, the members of the cohort retiring in 2005 receive in public pension benefits 44/45ths of what they would otherwise have received. The members of the cohort retiring in 2006 receive 43/45ths of what they would have received, and so on.
We finance the move to individual accounts via consumption taxation. Specifically, we completely eliminate those payroll taxes used to finance state pensions and impose a new consumption tax in each region to pay, over time, all accrued benefits. By 2078 all accrued pension benefits have been paid off, so the new consumption tax rates from that point on are zero.
The key feature of the reform is not ‘privatisation’ per se, but rather the intergenerational redistribution associated with moving to private accounts. The redistribution comprises three elements. First, the shift from payroll to consumption taxation reduces the tax burden on current and future workers and shifts it onto current retirees. Second, paying current workers (those working in 2004) when they reach retirement only their accrued state pension benefits rather than their projected benefits represents a cut in transfer payments that hurts those workers but benefits future workers who would otherwise have had to help pay for those benefits. Third, factor price changes arising from this policy help later generations at the cost of hurting earlier ones. Specifically, later generations benefit from higher real wages, while earlier generations lose from receiving lower returns on their assets.
There is no need to formally model the private accounts in which agents would be forced to save as part of this privatisation reform. The reason is that our agents face no liquidity constraints. Hence, they are free to borrow against their private account balances if they wish to consume more than their disposable income net of contributions to these accounts. Consequently, forcing our agents to save has no impact on their behaviour.[8]
In the US, the additional consumption tax rate needed to pay off accrued pension benefits is initially 6.8 per cent and gradually declines thereafter. The US payroll tax rate declines immediately by 7.8 percentage points. Over the transition, the payroll tax rate rises by 2.7 percentage points since expenses for health care and disability insurance grow.
In the EU, the added consumption tax rate has an initial value of 15.0 per cent and then declines. Because of this reform, the payroll tax is reduced by 14.6 percentage points in 2004 and rises to a maximum of 13.9 per cent in 2075. In Japan, the consumption tax rate is initially 11.1 per cent. It then rises to a maximum of 12.7 per cent in 2016 before declining. The payroll tax is 12.1 percentage points lower in 2004. And the maximum value reached is 15.7 per cent in 2050. Finally, the initial rate of the new consumption tax in China is 10.5 per cent. The payroll tax rate is initially reduced by 8 percentage points and rises to its maximum value of 5.5 per cent in 2075.
Of course, since part of the tax burden is shifted from payroll taxes towards consumption taxes, the burden on younger households falls and that on the elderly rises. The intergenerational redistribution associated with the consumption tax depresses aggregate consumption, which permits an increase in national saving and capital formation. The long-run consequences of this reform are dramatic in all three regions. Relative to the baseline simulations, the year 2100 capital stock increases by 87.6 per cent in the US, by 81.1 per cent in the EU, by 90.4 per cent in Japan, and by 83.2 per cent in China.
The higher capital stocks increase gross wages, which rise by by approximately 18 per cent in all four regions by 2100. The combination of higher gross wages and reduced payroll and wage taxes boosts net wages, which almost double in the four regions. The reductions in labour supply in the four regions, reported in Appendix Tables A1–A4, are a direct consequence of the positive income effects experienced by younger generations. Finally, capital accumulation leads to lower year-2100 interest rates.
Of course, the advantageous macroeconomic effects of privatisation come at a cost, which is shown in Table 12. The reform entails a major redistribution from older generations in all four economies towards younger and future generations. The intergenerational and intragenerational redistribution is less severe in the US compared to the EU, Japan and China, whose initial consumption tax rates are much higher.
| Birth year | US income class | EU income class | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −4.72 | −2.88 | −1.01 | −8.92 | −6.14 | −3.39 | |
| 1930 | −5.14 | −3.19 | −1.08 | −9.06 | −6.39 | −3.73 | |
| 1940 | −5.73 | −3.82 | −1.48 | −9.42 | −6.67 | −3.73 | |
| 1950 | −6.31 | −4.17 | −2.11 | −9.06 | −6.22 | −3.12 | |
| 1960 | −4.50 | −3.17 | −2.09 | −5.82 | −4.05 | −3.05 | |
| 1970 | −1.69 | −1.19 | −1.57 | −2.40 | −1.29 | −2.60 | |
| 1980 | 1.22 | 1.18 | −0.34 | 0.97 | 1.51 | −1.59 | |
| 1990 | 3.67 | 2.99 | 0.73 | 5.19 | 5.36 | 0.22 | |
| 2000 | 7.10 | 5.28 | 1.80 | 11.93 | 10.22 | 1.77 | |
| 2010 | 10.84 | 7.60 | 2.72 | 19.36 | 15.48 | 3.31 | |
| 2020 | 14.59 | 9.89 | 3.48 | 26.30 | 20.25 | 4.62 | |
| 2030 | 18.27 | 12.21 | 4.22 | 30.92 | 23.49 | 5.50 | |
| Japan income class | China income class | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| 1920 | −8.12 | −5.31 | −2.32 | −7.11 | −6.34 | −4.36 | |
| 1930 | −8.84 | −5.78 | −2.42 | −6.73 | −6.01 | −4.12 | |
| 1940 | −9.49 | −6.60 | −3.25 | −7.14 | −6.43 | −4.48 | |
| 1950 | −6.01 | −4.37 | −2.81 | −9.38 | −8.07 | −5.68 | |
| 1960 | −1.94 | −1.62 | −2.45 | −8.63 | −7.02 | −4.49 | |
| 1970 | 0.35 | 0.55 | −2.10 | −7.01 | −5.71 | −3.47 | |
| 1980 | 2.20 | 2.31 | −1.29 | −5.52 | −4.69 | −2.50 | |
| 1990 | 4.56 | 4.62 | −0.15 | −2.17 | −2.54 | −2.37 | |
| 2000 | 8.29 | 7.09 | 0.61 | 5.13 | 2.71 | −0.51 | |
| 2010 | 12.78 | 9.99 | 1.35 | 12.82 | 8.31 | 2.74 | |
| 2020 | 17.83 | 13.38 | 2.12 | 17.11 | 10.89 | 3.81 | |
| 2030 | 21.54 | 15.90 | 2.64 | 21.21 | 13.34 | 4.65 | |
The elderly are hurt because they are now forced to pay for their pension benefits via the consumption tax. Younger and future generations benefit enormously from the policy since they face much lower payroll tax burdens during their working years and experience much higher wages. Consider middle-income agents in the US. The oldest such agents included in Table 12 – those born in 1920 – experience a 2.9 per cent reduction in welfare. In contrast, the youngest such agents included in the table – those born in 2030 – enjoy a 12.2 per cent rise in welfare. For the other regions, corresponding welfare losses and gains experienced by the 1920 and 2030 middle classes are 6.1 per cent and 23.5 per cent in the EU, 5.3 per cent and 15.9 per cent in Japan, and 6.3 per cent and 13.3 per cent in China.
Another key feature of Table 12 is that, among those who are initially elderly, the poor experience larger welfare losses than the middle-class or the rich. The explanation for this differential welfare loss is that both the poor and rich elderly are constrained with respect to their consumption of leisure because they are both fully retired. However, the rich elderly are consuming a lot more than the poor. Hence, while both the rich and the poor experience roughly the same percentage reduction in consumption from the imposition of the consumption tax, the impact on their utilities are not the same because: (a) their initial consumption-leisure ratios differ; and (b) utility is not separable with respect to the two arguments.
9. Conclusion
The developed world and China all face enormous demographic changes which will greatly challenge their already overly stressed fiscal institutions. Fortunately, our dynamic life-cycle model suggests there may be a macroeconomic silver lining to this very grey demographic cloud. The silver lining is China, whose continued rapid acquisition of technology and human capital and extraordinarily high rate of saving can dramatically raise the world's supply of capital. Assuming the developed world's capital market remains open, China will gradually become the developed world's major source of capital.
Indeed, assuming China attains the developed world's living standard by the middle of this century and also maintains its very high propensity to save, it will raise real wages in the developed world by 40 per cent. This is over and above real wage increases arising from technological change. Even were China to gradually adopt Western spending habits, real wages at mid century will still be 16 per cent higher than is currently the case. This again is above and beyond what technological change can be expected to deliver.
Moreover, China's contribution to the developed world's own development is positive in both the short run and the long run. Even though capital initially moves from the developed world to China, there are no major short-run reductions in developed-world real wages. The reason is that the prospect of higher future real wages leads developed-world workers to supply less current labour. This keeps initial developed-world capital-labour ratios and the real wages on which they depend from falling.
Absent China, our model suggests a very gradual decline in the developed world's capital intensivity, with real wages per unit of human capital 4 per cent lower at the end of the century than they are today. This is much less ominous news than we delivered in previous studies that omitted China. The reason is that we now incorporate government investment, which implies more developed-world saving.
In addition to examining China's role in world economic development and incorporating government investment, this study has entertained a variety of demographic and fiscal scenarios. Our demographic scenarios, which we apply to all four regions simultaneously, are: (a) maintaining fertility rates at their current, generally very low, levels for much longer than governments now project; (b) increasing longevity at faster than projected rates; and (c) immediately and permanently doubling rates of immigration.
Each of these demographic changes has very little impact on the overall macroeconomic situation, but each makes a non-trivial difference to where payroll tax rates end up. For example, Japan's payroll tax rate ends up 25 per cent higher at the end of the century if its fertility rate fails to rise to the now-projected 2050 level; the EU's payroll tax rate ends 5 percentage points higher in 2030 if EU life expectancy rises by three years more by 2050 than now expected; and the US payroll tax rate is reduced by 1 per cent in 2050 if it doubles its rate of immigration.
Our five policy simulations: raised the rate of growth of health expenditures over the next quarter-century; switched, at the margin, to income-tax finance of government pension benefits; financed future increases in aggregate pension benefits via increases in public debt rather than payroll taxes; reduced generosity of welfare benefits to retirees; and privatised state pension systems by paying off accrued pension benefits with a consumption tax. Each of these policies has important macroeconomic impacts. But the one with the biggest impact is the privatisation of state pensions, which more than doubles long-run ratios of physical capital per unit of human capital and raises long-run real wages by roughly a quarter. The policy delivers major benefits to future generations, both because of the higher wages they earn and the dramatically lower payroll tax rates that they face.
To conclude, there is no reason to believe that China is currently eating our lunch or will do so in the near future. On the contrary, there is good reason to believe that China is in the process of taking us to dinner by slowly but surely becoming the world's biggest saver and the developed world's major supplier of capital.
Appendix A
| Year | Index of national income | Index of capital stock | Index of labour supply | Current account/ national income |
Index of pre-tax wage | Interest rate | Social security payroll tax rate | Average wage tax | |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 2004 | 1.00 | 1.00 | 1.00 | 0.028 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.13 | 1.19 | 1.12 | −0.039 | 1.02 | 0.093 | 0.119 | 0.070 | |
| 2020 | 1.47 | 1.92 | 1.35 | −0.144 | 1.09 | 0.075 | 0.138 | 0.069 | |
| 2030 | 1.89 | 3.04 | 1.62 | −0.168 | 1.17 | 0.061 | 0.164 | 0.078 | |
| 2050 | 2.63 | 4.11 | 2.28 | 0.054 | 1.16 | 0.063 | 0.171 | 0.093 | |
| 2075 | 3.29 | 4.05 | 3.08 | 0.037 | 1.07 | 0.080 | 0.207 | 0.080 | |
| 2100 | 4.11 | 4.67 | 3.96 | 0.017 | 1.04 | 0.087 | 0.230 | 0.068 | |
| Constant time preference in China | 2004 | 1.00 | 1.00 | 1.00 | 0.024 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.13 | 1.20 | 1.11 | −0.053 | 1.02 | 0.093 | 0.119 | 0.070 | |
| 2020 | 1.46 | 1.99 | 1.33 | −0.210 | 1.11 | 0.072 | 0.138 | 0.069 | |
| 2030 | 1.90 | 3.50 | 1.57 | −0.323 | 1.22 | 0.054 | 0.163 | 0.078 | |
| 2050 | 3.02 | 8.39 | 2.17 | −0.253 | 1.40 | 0.036 | 0.151 | 0.087 | |
| 2075 | 4.62 | 18.45 | 2.95 | −0.171 | 1.58 | 0.025 | 0.153 | 0.081 | |
| 2100 | 6.09 | 26.09 | 3.78 | −0.084 | 1.62 | 0.023 | 0.164 | 0.078 | |
| Lower technology growth in China | 2004 | 0.98 | 0.98 | 0.99 | −0.063 | 1.00 | 0.099 | 0.117 | 0.074 |
| 2010 | 1.17 | 1.35 | 1.11 | −0.115 | 1.05 | 0.085 | 0.114 | 0.073 | |
| 2020 | 1.55 | 2.28 | 1.37 | −0.158 | 1.14 | 0.067 | 0.130 | 0.077 | |
| 2030 | 1.95 | 3.41 | 1.63 | −0.142 | 1.20 | 0.056 | 0.160 | 0.085 | |
| 2050 | 2.67 | 4.29 | 2.29 | 0.059 | 1.17 | 0.061 | 0.171 | 0.096 | |
| 2075 | 3.24 | 3.86 | 3.07 | 0.044 | 1.06 | 0.083 | 0.211 | 0.082 | |
| 2100 | 4.06 | 4.50 | 3.94 | 0.016 | 1.03 | 0.089 | 0.233 | 0.069 | |
| Constant fertility in all regions | 2004 | 1.00 | 1.00 | 1.00 | 0.028 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.13 | 1.19 | 1.12 | −0.039 | 1.02 | 0.093 | 0.119 | 0.070 | |
| 2020 | 1.47 | 1.92 | 1.35 | −0.147 | 1.09 | 0.075 | 0.138 | 0.070 | |
| 2030 | 1.89 | 3.06 | 1.62 | −0.180 | 1.17 | 0.061 | 0.164 | 0.080 | |
| 2050 | 2.73 | 4.34 | 2.35 | 0.033 | 1.16 | 0.062 | 0.166 | 0.098 | |
| 2075 | 3.69 | 4.67 | 3.43 | 0.024 | 1.08 | 0.078 | 0.188 | 0.093 | |
| 2100 | 4.81 | 5.42 | 4.64 | 0.033 | 1.04 | 0.087 | 0.209 | 0.079 | |
| Higher life expectancy in all regions | 2004 | 1.00 | 1.00 | 1.00 | 0.024 | 1.00 | 0.098 | 0.116 | 0.077 |
| 2010 | 1.14 | 1.22 | 1.12 | −0.046 | 1.02 | 0.092 | 0.119 | 0.070 | |
| 2020 | 1.49 | 2.02 | 1.36 | −0.152 | 1.10 | 0.073 | 0.138 | 0.069 | |
| 2030 | 1.93 | 3.29 | 1.63 | −0.182 | 1.19 | 0.058 | 0.168 | 0.077 | |
| 2050 | 2.75 | 4.72 | 2.31 | 0.043 | 1.19 | 0.057 | 0.184 | 0.090 | |
| 2075 | 3.42 | 4.46 | 3.14 | 0.052 | 1.09 | 0.075 | 0.228 | 0.079 | |
| 2100 | 4.23 | 4.92 | 4.05 | 0.020 | 1.05 | 0.085 | 0.254 | 0.065 | |
| Doubling immigration in all regions | 2004 | 1.01 | 1.00 | 1.00 | 0.026 | 1.00 | 0.098 | 0.116 | 0.076 |
| 2010 | 1.17 | 1.22 | 1.14 | −0.044 | 1.02 | 0.093 | 0.117 | 0.069 | |
| 2020 | 1.57 | 2.04 | 1.45 | −0.148 | 1.09 | 0.076 | 0.131 | 0.069 | |
| 2030 | 2.10 | 3.34 | 1.80 | −0.170 | 1.17 | 0.062 | 0.153 | 0.079 | |
| 2050 | 3.13 | 4.84 | 2.71 | 0.048 | 1.16 | 0.064 | 0.160 | 0.091 | |
| 2075 | 4.17 | 5.14 | 3.90 | 0.035 | 1.07 | 0.080 | 0.198 | 0.078 | |
| 2100 | 5.41 | 6.22 | 5.18 | 0.021 | 1.05 | 0.085 | 0.224 | 0.063 | |
| Health expenditures rise by 3 per cent in all regions | 2004 | 1.00 | 1.00 | 1.00 | 0.028 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.14 | 1.20 | 1.12 | −0.039 | 1.02 | 0.093 | 0.120 | 0.070 | |
| 2020 | 1.47 | 1.93 | 1.35 | −0.140 | 1.09 | 0.075 | 0.143 | 0.069 | |
| 2030 | 1.89 | 3.05 | 1.62 | −0.166 | 1.17 | 0.061 | 0.177 | 0.079 | |
| 2050 | 2.63 | 4.06 | 2.29 | 0.054 | 1.15 | 0.064 | 0.184 | 0.094 | |
| 2075 | 3.28 | 3.96 | 3.09 | 0.037 | 1.06 | 0.081 | 0.224 | 0.082 | |
| 2100 | 4.10 | 4.55 | 3.97 | 0.017 | 1.03 | 0.089 | 0.248 | 0.070 | |
| Financing benefits by general tax revenues | 2004 | 1.00 | 1.00 | 1.00 | 0.028 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.13 | 1.20 | 1.12 | −0.039 | 1.02 | 0.093 | 0.116 | 0.073 | |
| 2020 | 1.47 | 1.92 | 1.35 | −0.144 | 1.09 | 0.075 | 0.116 | 0.090 | |
| 2030 | 1.88 | 3.05 | 1.61 | −0.172 | 1.17 | 0.061 | 0.116 | 0.125 | |
| 2050 | 2.63 | 4.13 | 2.28 | 0.054 | 1.16 | 0.063 | 0.116 | 0.146 | |
| 2075 | 3.27 | 4.04 | 3.07 | 0.037 | 1.07 | 0.080 | 0.116 | 0.169 | |
| 2100 | 4.07 | 4.59 | 3.93 | 0.018 | 1.04 | 0.087 | 0.116 | 0.178 | |
| Financing benefits by debt | 2004 | 1.00 | 1.00 | 1.00 | 0.031 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.13 | 1.18 | 1.11 | −0.039 | 1.01 | 0.094 | 0.116 | 0.070 | |
| 2020 | 1.47 | 1.88 | 1.35 | −0.146 | 1.09 | 0.077 | 0.116 | 0.069 | |
| 2030 | 1.86 | 2.99 | 1.60 | −0.164 | 1.17 | 0.061 | 0.166 | 0.098 | |
| 2050 | 2.61 | 3.91 | 2.29 | 0.044 | 1.14 | 0.066 | 0.173 | 0.116 | |
| 2075 | 3.24 | 3.74 | 3.10 | 0.035 | 1.05 | 0.085 | 0.210 | 0.123 | |
| 2100 | 4.03 | 4.21 | 3.99 | 0.016 | 1.01 | 0.094 | 0.234 | 0.119 | |
| Cut in replacement rates in all regions | 2004 | 1.00 | 1.00 | 1.01 | 0.029 | 1.00 | 0.098 | 0.116 | 0.078 |
| 2010 | 1.14 | 1.21 | 1.12 | −0.039 | 1.02 | 0.092 | 0.177 | 0.069 | |
| 2020 | 1.48 | 1.99 | 1.35 | −0.143 | 1.10 | 0.073 | 0.126 | 0.068 | |
| 2030 | 1.91 | 3.19 | 1.62 | −0.169 | 1.18 | 0.059 | 0.144 | 0.076 | |
| 2050 | 2.66 | 4.39 | 2.26 | 0.054 | 1.18 | 0.060 | 0.148 | 0.088 | |
| 2075 | 3.35 | 4.46 | 3.06 | 0.034 | 1.10 | 0.074 | 0.176 | 0.076 | |
| 2100 | 4.21 | 5.21 | 3.94 | 0.016 | 1.07 | 0.079 | 0.194 | 0.065 | |
| Privatising pensions | 2004 | 1.01 | 1.00 | 1.02 | 0.021 | 0.99 | 0.100 | 0.038 | 0.077 |
| 2010 | 1.17 | 1.29 | 1.13 | −0.047 | 1.03 | 0.089 | 0.039 | 0.068 | |
| 2020 | 1.54 | 2.26 | 1.36 | −0.144 | 1.13 | 0.067 | 0.044 | 0.065 | |
| 2030 | 1.99 | 3.77 | 1.62 | −0.171 | 1.24 | 0.052 | 0.054 | 0.071 | |
| 2050 | 2.81 | 5.79 | 2.22 | 0.050 | 1.27 | 0.048 | 0.052 | 0.076 | |
| 2075 | 3.68 | 7.01 | 2.99 | 0.018 | 1.24 | 0.052 | 0.060 | 0.062 | |
| 2100 | 4.71 | 8.76 | 3.85 | 0.010 | 1.23 | 0.053 | 0.065 | 0.054 |
| Year | Index of national income | Index of capital stock | Index of labour supply | Current account/ national income |
Index of pre-tax wage | Interest rate | Social security payroll tax rate | Average wage tax | |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 2004 | 1.42 | 1.38 | 1.45 | 0.083 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.53 | 1.57 | 1.53 | 0.032 | 1.01 | 0.093 | 0.265 | 0.060 | |
| 2020 | 1.79 | 2.27 | 1.67 | −0.052 | 1.08 | 0.075 | 0.286 | 0.051 | |
| 2030 | 2.03 | 3.17 | 1.76 | −0.083 | 1.16 | 0.061 | 0.327 | 0.058 | |
| 2050 | 2.28 | 3.44 | 2.00 | 0.031 | 1.14 | 0.063 | 0.381 | 0.071 | |
| 2075 | 2.57 | 3.06 | 2.44 | 0.014 | 1.06 | 0.080 | 0.380 | 0.079 | |
| 2100 | 3.19 | 3.50 | 3.11 | 0.020 | 1.03 | 0.087 | 0.367 | 0.074 | |
| Constant time preference in China | 2004 | 1.42 | 1.38 | 1.45 | 0.081 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.53 | 1.58 | 1.53 | 0.025 | 1.01 | 0.093 | 0.265 | 0.060 | |
| 2020 | 1.81 | 2.38 | 1.66 | −0.094 | 1.09 | 0.072 | 0.286 | 0.053 | |
| 2030 | 2.09 | 3.71 | 1.74 | −0.194 | 1.21 | 0.054 | 0.321 | 0.066 | |
| 2050 | 2.69 | 7.21 | 1.95 | −0.215 | 1.39 | 0.036 | 0.329 | 0.101 | |
| 2075 | 3.67 | 14.11 | 2.36 | −0.157 | 1.56 | 0.025 | 0.273 | 0.123 | |
| 2100 | 4.76 | 19.68 | 2.99 | −0.076 | 1.60 | 0.023 | 0.261 | 0.120 | |
| Lower technology growth in China | 2004 | 1.41 | 1.36 | 1.44 | 0.005 | 0.99 | 0.099 | 0.255 | 0.078 |
| 2010 | 1.58 | 1.78 | 1.53 | −0.035 | 1.04 | 0.085 | 0.255 | 0.071 | |
| 2020 | 1.89 | 2.71 | 1.69 | −0.069 | 1.12 | 0.067 | 0.272 | 0.072 | |
| 2030 | 2.11 | 3.57 | 1.79 | −0.057 | 1.19 | 0.056 | 0.317 | 0.075 | |
| 2050 | 2.31 | 3.60 | 2.01 | 0.037 | 1.16 | 0.061 | 0.377 | 0.081 | |
| 2075 | 2.54 | 2.93 | 2.44 | 0.022 | 1.05 | 0.083 | 0.385 | 0.082 | |
| 2100 | 3.15 | 3.38 | 3.10 | 0.020 | 1.02 | 0.089 | 0.369 | 0.074 | |
| Constant fertility in all regions | 2004 | 1.42 | 1.38 | 1.44 | 0.082 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.53 | 1.56 | 1.53 | 0.030 | 1.01 | 0.093 | 0.265 | 0.060 | |
| 2020 | 1.78 | 2.25 | 1.66 | −0.054 | 1.08 | 0.075 | 0.287 | 0.050 | |
| 2030 | 2.01 | 3.14 | 1.74 | −0.083 | 1.16 | 0.061 | 0.329 | 0.055 | |
| 2050 | 2.17 | 3.34 | 1.90 | 0.034 | 1.15 | 0.062 | 0.394 | 0.062 | |
| 2075 | 2.19 | 2.67 | 2.06 | 0.017 | 1.07 | 0.078 | 0.424 | 0.060 | |
| 2100 | 2.45 | 2.67 | 2.39 | 0.005 | 1.03 | 0.087 | 0.412 | 0.065 | |
| Higher life expectancy in all regions | 2004 | 1.43 | 1.38 | 1.45 | 0.081 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.55 | 1.60 | 1.54 | 0.029 | 1.01 | 0.092 | 0.264 | 0.061 | |
| 2020 | 1.83 | 2.40 | 1.69 | −0.056 | 1.09 | 0.073 | 0.286 | 0.053 | |
| 2030 | 2.09 | 3.44 | 1.78 | −0.090 | 1.18 | 0.058 | 0.330 | 0.059 | |
| 2050 | 2.39 | 3.98 | 2.04 | 0.022 | 1.18 | 0.057 | 0.397 | 0.069 | |
| 2075 | 2.68 | 3.39 | 2.50 | 0.026 | 1.08 | 0.075 | 0.402 | 0.079 | |
| 2100 | 3.29 | 3.70 | 3.18 | 0.023 | 1.04 | 0.085 | 0.390 | 0.072 | |
| Doubling immigration in all regions | 2004 | 1.43 | 1.38 | 1.45 | 0.082 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.55 | 1.58 | 1.55 | 0.030 | 1.00 | 0.093 | 0.263 | 0.060 | |
| 2020 | 1.85 | 2.32 | 1.72 | −0.052 | 1.08 | 0.076 | 0.281 | 0.052 | |
| 2030 | 2.14 | 3.30 | 1.86 | −0.084 | 1.15 | 0.062 | 0.317 | 0.060 | |
| 2050 | 2.53 | 3.79 | 2.22 | 0.032 | 1.14 | 0.064 | 0.360 | 0.075 | |
| 2075 | 3.02 | 3.61 | 2.86 | 0.016 | 1.06 | 0.080 | 0.364 | 0.079 | |
| 2100 | 3.89 | 4.33 | 3.77 | 0.023 | 1.03 | 0.085 | 0.356 | 0.069 | |
| Health expenditures rise by 3 per cent in all regions | 2004 | 1.43 | 1.38 | 1.45 | 0.084 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.54 | 1.58 | 1.54 | 0.033 | 1.01 | 0.093 | 0.270 | 0.061 | |
| 2020 | 1.80 | 2.29 | 1.68 | −0.050 | 1.08 | 0.075 | 0.303 | 0.053 | |
| 2030 | 2.04 | 3.18 | 1.77 | −0.086 | 1.16 | 0.061 | 0.359 | 0.061 | |
| 2050 | 2.30 | 3.43 | 2.02 | 0.026 | 1.14 | 0.064 | 0.413 | 0.078 | |
| 2075 | 2.59 | 3.03 | 2.48 | 0.011 | 1.05 | 0.081 | 0.412 | 0.090 | |
| 2100 | 3.22 | 3.46 | 3.17 | 0.017 | 1.02 | 0.089 | 0.399 | 0.087 | |
| Financing benefits by general tax revenues | 2004 | 1.42 | 1.38 | 1.45 | 0.084 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.53 | 1.57 | 1.53 | 0.032 | 1.01 | 0.093 | 0.253 | 0.071 | |
| 2020 | 1.79 | 2.27 | 1.67 | −0.051 | 1.08 | 0.075 | 0.253 | 0.081 | |
| 2030 | 2.02 | 3.17 | 1.75 | −0.085 | 1.16 | 0.061 | 0.253 | 0.124 | |
| 2050 | 2.26 | 3.44 | 1.98 | 0.028 | 1.15 | 0.063 | 0.253 | 0.184 | |
| 2075 | 2.56 | 3.06 | 2.43 | 0.013 | 1.06 | 0.080 | 0.253 | 0.195 | |
| 2100 | 3.17 | 3.46 | 3.10 | 0.021 | 1.03 | 0.087 | 0.253 | 0.178 | |
| Financing benefits by debt | 2004 | 1.42 | 1.38 | 1.44 | 0.080 | 0.99 | 0.098 | 0.253 | 0.080 |
| 2010 | 1.52 | 1.55 | 1.53 | 0.026 | 1.00 | 0.094 | 0.253 | 0.060 | |
| 2020 | 1.79 | 2.23 | 1.68 | −0.063 | 1.07 | 0.077 | 0.253 | 0.051 | |
| 2030 | 1.96 | 3.04 | 1.70 | −0.112 | 1.16 | 0.061 | 0.340 | 0.112 | |
| 2050 | 2.26 | 3.28 | 2.01 | 0.006 | 1.13 | 0.066 | 0.383 | 0.135 | |
| 2075 | 2.58 | 2.89 | 2.50 | −0.012 | 1.04 | 0.085 | 0.378 | 0.196 | |
| 2100 | 3.27 | 3.31 | 3.28 | −0.009 | 1.00 | 0.094 | 0.359 | 0.225 | |
| Cut in replacement rates in all regions | 2004 | 1.43 | 1.39 | 1.46 | 0.085 | 0.99 | 0.098 | 0.251 | 0.080 |
| 2010 | 1.55 | 1.60 | 1.54 | 0.036 | 1.01 | 0.092 | 0.260 | 0.060 | |
| 2020 | 1.82 | 2.36 | 1.68 | −0.044 | 1.09 | 0.073 | 0.267 | 0.050 | |
| 2030 | 2.06 | 3.32 | 1.76 | −0.074 | 1.17 | 0.059 | 0.293 | 0.055 | |
| 2050 | 2.29 | 3.66 | 1.98 | 0.040 | 1.17 | 0.060 | 0.332 | 0.061 | |
| 2075 | 2.59 | 3.33 | 2.39 | 0.017 | 1.09 | 0.074 | 0.333 | 0.062 | |
| 2100 | 3.22 | 3.86 | 3.05 | 0.022 | 1.06 | 0.079 | 0.320 | 0.057 | |
| Privatising pensions | 2004 | 1.46 | 1.40 | 1.49 | 0.097 | 0.98 | 0.100 | 0.107 | 0.085 |
| 2010 | 1.60 | 1.71 | 1.57 | 0.055 | 1.02 | 0.089 | 0.111 | 0.063 | |
| 2020 | 1.90 | 2.69 | 1.70 | −0.015 | 1.12 | 0.067 | 0.116 | 0.049 | |
| 2030 | 2.15 | 3.95 | 1.77 | −0.044 | 1.22 | 0.052 | 0.127 | 0.048 | |
| 2050 | 2.41 | 4.81 | 1.93 | 0.070 | 1.26 | 0.048 | 0.137 | 0.035 | |
| 2075 | 2.78 | 5.12 | 2.28 | 0.020 | 1.22 | 0.052 | 0.139 | 0.022 | |
| 2100 | 3.52 | 6.34 | 2.92 | 0.024 | 1.21 | 0.053 | 0.135 | 0.021 |
| Year | Index of national income | Index of capital stock | Index of labour supply | Current account/ national income |
Index of pre-tax wage | Interest rate | Social security payroll tax rate | Average wage tax | |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 2004 | 0.49 | 0.50 | 0.49 | 0.138 | 1.01 | 0.098 | 0.221 | 0.066 |
| 2010 | 0.50 | 0.53 | 0.49 | 0.082 | 1.02 | 0.093 | 0.257 | 0.043 | |
| 2020 | 0.54 | 0.72 | 0.49 | −0.050 | 1.10 | 0.075 | 0.299 | 0.027 | |
| 2030 | 0.60 | 1.00 | 0.52 | −0.070 | 1.18 | 0.061 | 0.301 | 0.031 | |
| 2050 | 0.60 | 0.95 | 0.52 | 0.060 | 1.17 | 0.063 | 0.359 | 0.022 | |
| 2075 | 0.61 | 0.77 | 0.57 | 0.027 | 1.08 | 0.080 | 0.354 | 0.026 | |
| 2100 | 0.71 | 0.83 | 0.69 | 0.028 | 1.05 | 0.087 | 0.328 | 0.027 | |
| Constant time preference in China | 2004 | 0.49 | 0.50 | 0.49 | 0.139 | 1.01 | 0.098 | 0.220 | 0.066 |
| 2010 | 0.50 | 0.54 | 0.49 | 0.081 | 1.03 | 0.093 | 0.256 | 0.043 | |
| 2020 | 0.55 | 0.76 | 0.49 | −0.085 | 1.11 | 0.072 | 0.295 | 0.028 | |
| 2030 | 0.63 | 1.17 | 0.51 | −0.172 | 1.23 | 0.054 | 0.291 | 0.039 | |
| 2050 | 0.72 | 2.03 | 0.51 | −0.180 | 1.41 | 0.036 | 0.304 | 0.051 | |
| 2075 | 0.89 | 3.62 | 0.56 | −0.127 | 1.59 | 0.025 | 0.256 | 0.067 | |
| 2100 | 1.10 | 4.82 | 0.68 | −0.050 | 1.63 | 0.023 | 0.227 | 0.065 | |
| Lower technology growth in China | 2004 | 0.48 | 0.49 | 0.48 | 0.057 | 1.00 | 0.099 | 0.224 | 0.067 |
| 2010 | 0.51 | 0.61 | 0.49 | 0.016 | 1.06 | 0.085 | 0.248 | 0.050 | |
| 2020 | 0.57 | 0.86 | 0.50 | −0.066 | 1.14 | 0.067 | 0.283 | 0.040 | |
| 2030 | 0.63 | 1.12 | 0.52 | −0.040 | 1.21 | 0.056 | 0.290 | 0.041 | |
| 2050 | 0.61 | 1.00 | 0.52 | 0.065 | 1.18 | 0.061 | 0.354 | 0.028 | |
| 2075 | 0.60 | 0.73 | 0.57 | 0.034 | 1.07 | 0.083 | 0.360 | 0.026 | |
| 2100 | 0.71 | 0.80 | 0.68 | 0.028 | 1.04 | 0.089 | 0.332 | 0.025 | |
| Constant fertility in all regions | 2004 | 0.49 | 0.50 | 0.49 | 0.138 | 1.01 | 0.098 | 0.222 | 0.066 |
| 2010 | 0.49 | 0.53 | 0.49 | 0.081 | 1.02 | 0.093 | 0.257 | 0.043 | |
| 2020 | 0.54 | 0.71 | 0.49 | −0.053 | 1.10 | 0.075 | 0.300 | 0.026 | |
| 2030 | 0.60 | 0.99 | 0.51 | −0.068 | 1.18 | 0.061 | 0.302 | 0.027 | |
| 2050 | 0.56 | 0.91 | 0.48 | 0.069 | 1.17 | 0.062 | 0.378 | 0.009 | |
| 2075 | 0.48 | 0.62 | 0.44 | 0.021 | 1.09 | 0.078 | 0.425 | −0.004 | |
| 2100 | 0.48 | 0.55 | 0.46 | −0.010 | 1.05 | 0.087 | 0.400 | 0.007 | |
| Higher life expectancy in all regions | 2004 | 0.49 | 0.50 | 0.49 | 0.142 | 1.00 | 0.098 | 0.220 | 0.067 |
| 2010 | 0.50 | 0.55 | 0.49 | 0.087 | 1.03 | 0.092 | 0.255 | 0.044 | |
| 2020 | 0.55 | 0.76 | 0.50 | −0.047 | 1.11 | 0.073 | 0.298 | 0.027 | |
| 2030 | 0.62 | 1.08 | 0.52 | −0.072 | 1.20 | 0.058 | 0.305 | 0.030 | |
| 2050 | 0.63 | 1.10 | 0.53 | 0.059 | 1.20 | 0.057 | 0.367 | 0.019 | |
| 2075 | 0.63 | 0.85 | 0.58 | 0.036 | 1.10 | 0.075 | 0.382 | 0.021 | |
| 2100 | 0.73 | 0.87 | 0.70 | 0.033 | 1.06 | 0.085 | 0.350 | 0.021 | |
| Doubling immigration in all regions | 2004 | 0.49 | 0.50 | 0.49 | 0.138 | 1.01 | 0.098 | 0.221 | 0.066 |
| 2010 | 0.50 | 0.54 | 0.49 | 0.083 | 1.02 | 0.093 | 0.256 | 0.043 | |
| 2020 | 0.54 | 0.72 | 0.50 | −0.048 | 1.10 | 0.076 | 0.296 | 0.027 | |
| 2030 | 0.62 | 1.00 | 0.53 | −0.068 | 1.17 | 0.062 | 0.297 | 0.031 | |
| 2050 | 0.63 | 0.99 | 0.54 | 0.058 | 1.16 | 0.064 | 0.349 | 0.024 | |
| 2075 | 0.66 | 0.83 | 0.62 | 0.028 | 1.08 | 0.080 | 0.343 | 0.027 | |
| 2100 | 0.79 | 0.94 | 0.76 | 0.030 | 1.05 | 0.085 | 0.320 | 0.026 | |
| Health expenditures rise by 3 per cent in all regions | 2004 | 0.49 | 0.50 | 0.49 | 0.139 | 1.01 | 0.098 | 0.221 | 0.066 |
| 2010 | 0.50 | 0.54 | 0.49 | 0.085 | 1.02 | 0.093 | 0.261 | 0.044 | |
| 2020 | 0.54 | 0.73 | 0.50 | −0.049 | 1.10 | 0.075 | 0.316 | 0.028 | |
| 2030 | 0.61 | 1.00 | 0.52 | −0.075 | 1.18 | 0.061 | 0.336 | 0.032 | |
| 2050 | 0.60 | 0.95 | 0.52 | 0.055 | 1.16 | 0.064 | 0.399 | 0.027 | |
| 2075 | 0.62 | 0.76 | 0.58 | 0.023 | 1.07 | 0.081 | 0.394 | 0.034 | |
| 2100 | 0.72 | 0.82 | 0.70 | 0.027 | 1.04 | 0.089 | 0.365 | 0.036 | |
| Financing benefits by general tax revenues | 2004 | 0.49 | 0.50 | 0.49 | 0.142 | 1.01 | 0.098 | 0.221 | 0.065 |
| 2010 | 0.49 | 0.53 | 0.49 | 0.086 | 1.02 | 0.093 | 0.221 | 0.072 | |
| 2020 | 0.54 | 0.72 | 0.49 | −0.052 | 1.10 | 0.075 | 0.221 | 0.091 | |
| 2030 | 0.60 | 1.00 | 0.51 | −0.074 | 1.18 | 0.061 | 0.221 | 0.098 | |
| 2050 | 0.60 | 0.96 | 0.51 | 0.060 | 1.17 | 0.063 | 0.221 | 0.140 | |
| 2075 | 0.61 | 0.77 | 0.57 | 0.025 | 1.08 | 0.080 | 0.221 | 0.142 | |
| 2100 | 0.71 | 0.82 | 0.68 | 0.030 | 1.05 | 0.087 | 0.221 | 0.120 | |
| Financing benefits by debt | 2004 | 0.48 | 0.50 | 0.48 | 0.125 | 1.01 | 0.098 | 0.221 | 0.065 |
| 2010 | 0.49 | 0.53 | 0.48 | 0.061 | 1.02 | 0.094 | 0.221 | 0.043 | |
| 2020 | 0.54 | 0.71 | 0.50 | −0.076 | 1.09 | 0.077 | 0.221 | 0.027 | |
| 2030 | 0.55 | 0.91 | 0.47 | −0.161 | 1.18 | 0.061 | 0.328 | 0.170 | |
| 2050 | 0.61 | 0.94 | 0.53 | 0.004 | 1.15 | 0.066 | 0.354 | 0.158 | |
| 2075 | 0.64 | 0.76 | 0.61 | −0.028 | 1.05 | 0.085 | 0.339 | 0.265 | |
| 2100 | 0.78 | 0.84 | 0.77 | −0.030 | 1.02 | 0.094 | 0.302 | 0.331 | |
| Cut in replacement rates in all regions | 2004 | 0.49 | 0.50 | 0.49 | 0.131 | 1.00 | 0.098 | 0.222 | 0.066 |
| 2010 | 0.50 | 0.54 | 0.49 | 0.072 | 1.03 | 0.092 | 0.256 | 0.044 | |
| 2020 | 0.54 | 0.75 | 0.49 | −0.063 | 1.11 | 0.073 | 0.295 | 0.029 | |
| 2030 | 0.61 | 1.05 | 0.52 | −0.080 | 1.19 | 0.059 | 0.296 | 0.034 | |
| 2050 | 0.61 | 1.03 | 0.52 | 0.057 | 1.19 | 0.060 | 0.352 | 0.026 | |
| 2075 | 0.63 | 0.86 | 0.57 | 0.018 | 1.11 | 0.074 | 0.345 | 0.033 | |
| 2100 | 0.75 | 0.94 | 0.70 | 0.021 | 1.08 | 0.079 | 0.315 | 0.038 | |
| Privatising pensions | 2004 | 0.49 | 0.50 | 0.49 | 0.134 | 1.00 | 0.100 | 0.100 | 0.071 |
| 2010 | 0.51 | 0.58 | 0.49 | 0.081 | 1.04 | 0.089 | 0.110 | 0.047 | |
| 2020 | 0.57 | 0.85 | 0.50 | −0.042 | 1.14 | 0.067 | 0.129 | 0.032 | |
| 2030 | 0.64 | 1.24 | 0.52 | −0.064 | 1.24 | 0.052 | 0.138 | 0.033 | |
| 2050 | 0.65 | 1.36 | 0.51 | 0.068 | 1.28 | 0.048 | 0.157 | 0.014 | |
| 2075 | 0.69 | 1.33 | 0.55 | 0.005 | 1.25 | 0.052 | 0.155 | 0.016 | |
| 2100 | 0.83 | 1.58 | 0.68 | 0.008 | 1.24 | 0.053 | 0.143 | 0.024 |
| Year | Index of national income | Index of capital stock | Index of labour supply | Current account/ national income |
Index of pre-tax wage | Interest rate | Social security payroll tax rate | Average wage tax | |
|---|---|---|---|---|---|---|---|---|---|
| Baseline | 2004 | 1.33 | 1.52 | 8.90 | −0.161 | 0.15 | 0.098 | 0.111 | 0.071 |
| 2010 | 2.29 | 2.76 | 9.78 | −0.020 | 0.24 | 0.093 | 0.082 | 0.088 | |
| 2020 | 4.23 | 6.31 | 10.13 | 0.078 | 0.42 | 0.075 | 0.085 | 0.076 | |
| 2030 | 5.82 | 10.71 | 8.99 | 0.091 | 0.65 | 0.061 | 0.115 | 0.043 | |
| 2050 | 8.52 | 15.15 | 7.87 | −0.029 | 1.09 | 0.063 | 0.189 | −0.015 | |
| 2075 | 9.57 | 13.44 | 8.62 | −0.018 | 1.12 | 0.080 | 0.269 | −0.002 | |
| 2100 | 11.31 | 14.65 | 10.47 | −0.014 | 1.09 | 0.087 | 0.277 | 0.019 | |
| Constant time preference in China | 2004 | 1.33 | 1.52 | 8.95 | −0.155 | 0.15 | 0.098 | 0.111 | 0.073 |
| 2010 | 2.33 | 2.82 | 9.92 | −0.007 | 0.24 | 0.093 | 0.082 | 0.092 | |
| 2020 | 4.56 | 7.06 | 10.77 | 0.115 | 0.43 | 0.072 | 0.080 | 0.094 | |
| 2030 | 7.01 | 14.62 | 10.38 | 0.161 | 0.68 | 0.054 | 0.099 | 0.086 | |
| 2050 | 12.12 | 38.24 | 9.27 | 0.121 | 1.32 | 0.036 | 0.149 | 0.063 | |
| 2075 | 14.80 | 67.12 | 9.05 | 0.100 | 1.65 | 0.025 | 0.224 | 0.013 | |
| 2100 | 17.66 | 86.13 | 10.54 | 0.053 | 1.69 | 0.023 | 0.260 | −0.010 | |
| Lower technology growth in China | 2004 | 1.39 | 1.58 | 9.36 | 0.020 | 0.15 | 0.099 | 0.110 | 0.097 |
| 2010 | 1.90 | 2.52 | 10.30 | 0.095 | 0.19 | 0.085 | 0.096 | 0.089 | |
| 2020 | 2.80 | 4.71 | 11.00 | 0.147 | 0.26 | 0.067 | 0.122 | 0.058 | |
| 2030 | 3.40 | 6.77 | 10.31 | 0.124 | 0.33 | 0.056 | 0.151 | 0.012 | |
| 2050 | 4.48 | 8.21 | 9.99 | −0.063 | 0.45 | 0.061 | 0.224 | −0.054 | |
| 2075 | 5.02 | 6.83 | 11.54 | −0.043 | 0.44 | 0.083 | 0.282 | −0.016 | |
| 2100 | 6.00 | 7.57 | 14.11 | −0.025 | 0.43 | 0.089 | 0.283 | 0.016 | |
| Constant fertility in all regions | 2004 | 1.33 | 1.52 | 8.91 | −0.160 | 0.15 | 0.098 | 0.111 | 0.071 |
| 2010 | 2.29 | 2.76 | 9.78 | −0.018 | 0.24 | 0.093 | 0.082 | 0.088 | |
| 2020 | 4.23 | 6.29 | 10.12 | 0.081 | 0.42 | 0.075 | 0.085 | 0.076 | |
| 2030 | 5.80 | 10.68 | 8.96 | 0.095 | 0.65 | 0.061 | 0.115 | 0.043 | |
| 2050 | 8.27 | 14.95 | 7.60 | −0.025 | 1.09 | 0.062 | 0.193 | −0.018 | |
| 2075 | 8.57 | 12.35 | 7.66 | −0.016 | 1.13 | 0.078 | 0.293 | −0.012 | |
| 2100 | 9.35 | 12.03 | 8.68 | 0.018 | 1.08 | 0.087 | 0.305 | 0.012 | |
| Higher life expectancy in all regions | 2004 | 1.33 | 1.52 | 8.96 | −0.157 | 0.15 | 0.098 | 0.111 | 0.073 |
| 2010 | 2.32 | 2.82 | 9.85 | −0.015 | 0.24 | 0.092 | 0.083 | 0.090 | |
| 2020 | 4.33 | 6.67 | 10.24 | 0.082 | 0.43 | 0.073 | 0.086 | 0.079 | |
| 2030 | 6.01 | 11.65 | 9.13 | 0.097 | 0.66 | 0.058 | 0.117 | 0.047 | |
| 2050 | 8.94 | 17.48 | 8.01 | −0.023 | 1.12 | 0.057 | 0.202 | −0.015 | |
| 2075 | 10.00 | 14.88 | 8.84 | −0.027 | 1.14 | 0.075 | 0.303 | −0.013 | |
| 2100 | 11.65 | 15.44 | 10.71 | −0.016 | 1.10 | 0.085 | 0.318 | 0.017 | |
| Doubling immigration in all regions | 2004 | 1.33 | 1.52 | 8.90 | −0.159 | 0.15 | 0.098 | 0.111 | 0.071 |
| 2010 | 2.28 | 2.74 | 9.75 | −0.016 | 0.24 | 0.093 | 0.083 | 0.089 | |
| 2020 | 4.20 | 6.21 | 10.07 | 0.085 | 0.42 | 0.076 | 0.085 | 0.076 | |
| 2030 | 5.73 | 10.43 | 8.89 | 0.101 | 0.65 | 0.062 | 0.117 | 0.042 | |
| 2050 | 8.27 | 14.61 | 7.67 | −0.032 | 1.09 | 0.064 | 0.192 | −0.017 | |
| 2075 | 9.16 | 12.91 | 8.26 | −0.023 | 1.12 | 0.080 | 0.273 | −0.003 | |
| 2100 | 10.79 | 14.19 | 9.95 | −0.021 | 1.09 | 0.085 | 0.278 | 0.021 | |
| Health expenditures rise by 3 per cent in all regions | 2004 | 1.33 | 1.51 | 8.91 | −0.163 | 0.15 | 0.098 | 0.111 | 0.071 |
| 2010 | 2.29 | 2.77 | 9.78 | −0.022 | 0.24 | 0.093 | 0.084 | 0.089 | |
| 2020 | 4.25 | 6.35 | 10.15 | 0.076 | 0.42 | 0.075 | 0.090 | 0.077 | |
| 2030 | 5.94 | 10.73 | 9.02 | 0.092 | 0.65 | 0.061 | 0.150 | 0.045 | |
| 2050 | 8.53 | 15.00 | 7.92 | −0.028 | 1.08 | 0.064 | 0.238 | −0.012 | |
| 2075 | 9.57 | 13.17 | 8.68 | −0.017 | 1.11 | 0.081 | 0.303 | 0.001 | |
| 2100 | 11.30 | 14.30 | 10.54 | −0.013 | 1.08 | 0.089 | 0.285 | 0.022 | |
| Financing benefits by general tax revenues | 2004 | 1.32 | 1.52 | 8.90 | −0.164 | 0.15 | 0.098 | 0.111 | 0.071 |
| 2010 | 2.29 | 2.76 | 9.79 | −0.021 | 0.24 | 0.093 | 0.111 | 0.063 | |
| 2020 | 4.25 | 6.34 | 10.16 | 0.078 | 0.42 | 0.075 | 0.111 | 0.053 | |
| 2030 | 5.84 | 10.78 | 9.00 | 0.093 | 0.65 | 0.061 | 0.111 | 0.047 | |
| 2050 | 8.47 | 15.15 | 7.81 | −0.029 | 1.09 | 0.063 | 0.111 | 0.060 | |
| 2075 | 9.43 | 13.27 | 8.49 | −0.018 | 1.12 | 0.080 | 0.111 | 0.149 | |
| 2100 | 11.16 | 14.33 | 10.36 | −0.014 | 1.08 | 0.087 | 0.111 | 0.176 | |
| Financing benefits by debt | 2004 | 1.33 | 1.52 | 8.91 | −0.154 | 0.15 | 0.098 | 0.111 | 0.071 |
| 2010 | 2.28 | 2.73 | 9.77 | −0.012 | 0.23 | 0.094 | 0.083 | 0.088 | |
| 2020 | 4.21 | 6.16 | 10.12 | 0.087 | 0.42 | 0.077 | 0.085 | 0.075 | |
| 2030 | 5.81 | 10.62 | 8.99 | 0.106 | 0.65 | 0.061 | 0.115 | 0.043 | |
| 2050 | 8.40 | 14.37 | 7.87 | −0.016 | 1.07 | 0.066 | 0.191 | −0.018 | |
| 2075 | 9.27 | 12.21 | 8.54 | −0.007 | 1.09 | 0.085 | 0.274 | −0.010 | |
| 2100 | 10.79 | 12.87 | 10.27 | −0.001 | 1.06 | 0.094 | 0.283 | 0.007 | |
| Cut in replacement rates in all regions | 2004 | 1.33 | 1.51 | 8.94 | −0.162 | 0.15 | 0.098 | 0.111 | 0.072 |
| 2010 | 2.31 | 2.80 | 9.82 | −0.020 | 0.24 | 0.092 | 0.081 | 0.089 | |
| 2020 | 4.29 | 6.55 | 10.17 | 0.076 | 0.42 | 0.073 | 0.077 | 0.077 | |
| 2030 | 5.91 | 11.25 | 9.02 | 0.088 | 0.66 | 0.059 | 0.101 | 0.044 | |
| 2050 | 8.62 | 16.20 | 7.82 | −0.031 | 1.11 | 0.060 | 0.162 | −0.014 | |
| 2075 | 9.76 | 14.82 | 8.57 | −0.017 | 1.15 | 0.074 | 0.225 | −0.002 | |
| 2100 | 11.54 | 16.29 | 10.38 | −0.013 | 1.12 | 0.079 | 0.231 | 0.017 | |
| Privatising pensions | 2004 | 1.33 | 1.50 | 9.01 | −0.171 | 0.15 | 0.100 | 0.031 | 0.077 |
| 2010 | 2.36 | 2.98 | 9.91 | −0.031 | 0.24 | 0.089 | 0.028 | 0.094 | |
| 2020 | 4.49 | 7.51 | 10.33 | 0.061 | 0.44 | 0.067 | 0.030 | 0.083 | |
| 2030 | 6.28 | 13.55 | 9.19 | 0.076 | 0.69 | 0.052 | 0.039 | 0.052 | |
| 2050 | 9.18 | 21.55 | 7.74 | −0.038 | 1.19 | 0.048 | 0.052 | −0.007 | |
| 2075 | 10.69 | 23.20 | 8.33 | −0.012 | 1.29 | 0.052 | 0.055 | −0.002 | |
| 2100 | 12.66 | 26.84 | 9.95 | −0.011 | 1.28 | 0.053 | 0.053 | 0.010 |
Footnotes
We thank Charles Horioka, Bernd Raffelhüschen and Reinhold Schnabel for providing key data. Research support by the US Social Security Administration, Boston University, the Deutsche Forschungsgemeinschaft and the Universitatsbund Wuerzburg is gratefully acknowledged. [1]
Although the economic model starts in the year 2004, we chose the year 2000 as the initial year for the population projections due to data availability. [2]
The profile of Japanese average net wealth by age was provided by Charles Horioka, while the European age-specific average net wealth profiles were adjusted from German data provided by Reinhold Schnabel. We calculated a US age-net wealth profile using the 1998 Board of Governors of the Federal Reserve System Survey of Consumer Finances. For China, we adopted the Japanese age-net wealth profile. [3]
See OECD (2003a, p 178; 2003b, pp 71, 77). [4]
Actual values are calculated from European Commission (2005) and OECD (2003c). [5]
A more extensive analysis of how different population policies affect the future fiscal and economic development in the developed world is presented in Fehr et al (2004a, 2004b). [6]
After 2050, fertility rates gradually adjust again in order to achieve a zero long-run population growth rate. [7]
Including liquidity constraints would require solving our agents' utility maximisation problems using dynamic programming. Doing so would be much more time-consuming. It would also introduce a degree of approximation error into the solution that we avoid with our current formulation in which we find the solutions to the first-order conditions and budget constraints of our agents to a very high degree of precision using Gauss-Seidel iteration. [8]
References
Altig DE, AJ Auerbach, LJ Kotlikoff, KA Smetters and J Walliser (2001), ‘Simulating Fundamental Tax Reform in the United States’, American Economic Review, 91(3), pp 574–595.
Auerbach AJ and LJ Kotlikoff (1983), ‘An Examination of Empirical Tests of Social Security and Savings’, in E Helpman, A Razin and E Sadka (eds), Social Policy Evaluation: An Economic Perspective, Academic Press, New York, pp 161–179.
Auerbach AJ and LJ Kotlikoff (1987), Dynamic Fiscal Policy, Cambridge University Press, Cambridge.
Blöndal S and S Scarpetta (1998), ‘The Retirement Decision in OECD Countries’, OECD Economics Department Working Paper No 202.
Bohn H (2001), ‘Social Security and Demographic Uncertainty: The Risk-Sharing Properties of Alternative Policies’, in JY Campbell and M Feldstein (eds), Risk Aspects of Investment-Based Social Security Reform, University of Chicago Press, Chicago, pp 203–241.
Cooley TF and J Soares (1999a), ‘A Positive Theory of Social Security Based on Reputation’, Journal of Political Economy, 107(1), pp 135–160.
Cooley TF and J Soares (1999b), ‘Privatizing Social Security’, Review of Economic Dynamics, 2(3), pp 731–755.
De Nardi M, S Imrohoroglu and TJ Sargent (1999), ‘Projected U.S. Demographics and Social Security’, Review of Economic Dynamics, 2(3), pp 575–615.
Docteur E and H Oxley (2003), ‘Health-Care Systems: Lessons from the Reform Experience’, OECD Economics Department Working Paper No 374.
European Commission (2003), The Budgetary Challenges Posed by Ageing Populations, European Economy Reports and Studies No 42001, European Commission, Brussels.
European Commission (2005), ‘Statistical Annex to European Economy’, Spring. Available at <http://ec.europa.eu/economy_finance/publications/european_economy/statisticalannex0105_en.htm>.
Fehr H and C Habermann (2005), ‘Risk Sharing and Efficiency Implications of Progressive Pension Arrangements’, CESifo Working Paper No 1568.
Fehr H, G Halder, S Jokisch and LJ Kotlikoff (2003), ‘A Simulation Model for the Demographic Transition in the OECD – Data Requirements, Model Structure and Calibration’, Universität Würzburg Economic Papers No 45.
Fehr H, S Jokisch and LJ Kotlikoff (2004a), ‘Fertility, Mortality, and the Developed World's Demographic Transition’, CESifo Working Paper No 1326.
Fehr H, S Jokisch and LJ Kotlikoff (2004b), ‘The Role of Immigration in Dealing with the Developed World's Demographic Transition’, FinanzArchiv, 60(3), pp 296–324.
Fehr H, S Jokisch and LJ Kotlikoff (2005), ‘The Developed World's Demographic Transition – The Roles of Capital Flows, Immigration, and Policy’, in R Brooks and A Razin (eds), Social Security Reform – Financial and Political Issues in International Perspective, Cambridge University Press, Cambridge, p 11–43.
Feldstein MS (1974), ‘Social Security, Induced Retirement, and Aggregate Capital Accumulation’, Journal of Political Economy, 82(5), pp 905–926.
Heckman JJ, L Lochner and C Taber (1998), ‘Explaining Rising Wage Inequality: Explorations with a Dynamic General Equilibrium Model of Labor Earnings with Heterogeneous Agents’, Review of Economic Dynamics, 1(1), pp 1–58.
Huang H, S Imrohoroglu and TJ Sargent (1997), ‘Two Computational Experiments to Fund Social Security’, Macroeconomic Dynamics, 1(1), pp 7–44.
Hubbard GR and KL Judd (1987), ‘Social Security and Individual Welfare: Precautionary Saving, Borrowing Constraints, and the Payroll Tax’, American Economic Review, 77(4), pp 630–646.
Huggett M and G Ventura (1999), ‘On the Distributional Effects of Social Security Reform’, Review of Economic Dynamics, 2(3), pp 498–531.
Imrohoroglu A, S Imrohoroglu and DH Joines (1995), ‘A Life Cycle Analysis of Social Security’, Economic Theory, 6(1), pp 83–114.
Imrohoroglu A, S Imrohoroglu and DH Joines (1999), ‘Social Security in an Overlapping Generations Economy with Land’, Review of Economic Dynamics, 2(3), pp 638–665.
Kotlikoff LJ (1979), ‘Social Security and Equilibrium Capital Intensity’, Quarterly Journal of Economics, 93(2), pp 233–253.
Kotlikoff LJ (1996), ‘Privatizing Social Security: How It Works and Why It Matters’, in JM Poterba (ed), Tax Policy and the Economy, Vol 10, MIT Press, Cambridge, pp 1–32.
Kotlikoff LJ, KA Smetters and J Walliser (1998a), ‘The Economic Impact of Privatizing Social Security’, in H Siebert (ed), Redesigning Social Security, JCB Mohr, Tübingen, pp 327–348.
Kotlikoff LJ, KA Smetters and J Walliser (1998b), ‘Social Security: Privatization and Progressivity’, American Economic Review, 88(2), pp 137–141.
Kotlikoff LJ, KA Smetters and J Walliser (1999), ‘Privatizing Social Security in the U.S.: Comparing the Options’, Review of Economic Dynamics, 2(3), pp 532–574.
Kotlikoff LJ, KA Smetters and J Walliser (2001), ‘Finding a Way out of America's Demographic Dilemma’, NBER Working Paper No 8258.
Kotlikoff LJ, KA Smetters and J Walliser (2002), ‘Distributional Effects in a General Equilibrium Analysis of Social Security’, in MS Feldstein and JB Liebman (eds), The Distributional Aspects of Social Security and Social Security Reform, University of Chicago Press, Chicago, pp 327–371.
Nishiyama S and KA Smetters (2003), ‘Consumption Taxes and Economic Efficiency in a Stochastic OLG Economy’, NBER Working Paper No 9492.
OECD (2001), Ageing and Income: Financial Resources and Retirement in 9 OECD Countries, OECD, Paris.
OECD (2002), China in the World Economy: The Domestic Policy Challenges, OECD, Paris.
OECD (2003a), Education at a Glance: OECD Indicators 2003, OECD, Paris.
OECD (2003b), Financing Education – Investments and Returns: Analysis of the World Education Indicators 2002 edition, UNESCO and OECD, Paris.
OECD (2003c), Revenue Statistics 1965–2002, Vol 1, OECD, Paris.
Raffelhüschen B (1989), Anreizwirkungen des Systems der sozialen Alterssicherung – Eine dynamische Simulationsanalyse, Finanzwissenschaftliche Schriften, 40, Peter Lang, Frankfurt a.M.
Raffelhüschen B (1993), ‘Funding Social Security through Pareto-Optimal Conversion Policies’, Journal of Economics, Supplement 7, pp 105–131.
Seidman LS (1986), ‘A Phase-Down of Social Security: The Transition in a Life Cycle Growth Model’, National Tax Journal, 39(1), pp 97–107.
Siegel JJ (2005), The Future for Investors, Crown Business, New York.
Smetters K and J Walliser (2004), ‘Opting out of Social Security’, Journal of Public Economics, 88(7–8), pp 1295–1306.
Summers LH (1981), ‘Capital Taxation and Accumulation in a Life Cycle Growth Model’, American Economic Review, 71(4), pp 533–544.
Tuljapurkar S, N Li and C Boe (2000), ‘A Universal Pattern of Mortality Decline in the G7 Countries’, Nature, 405, pp 789–792.
UN Population Division (2003), World Population Prospects: The 2002 Revision, United Nations, New York. Available at <http://esa.un.org/unpp/>.
UN Population Division (2005), World Population Prospects: The 2004 Revision, United Nations, New York. Available at <http://esa.un.org/unpp/>.
Whitehouse E (2002), ‘Pension Systems in 15 Countries Compared: The Value of Entitlements’, Centre for Pensions and Superannuation Discussion Paper No 02/04.
WHO (World Health Organisation) (2004), The World Health Report 2004 – Changing History, World Health Organisation, Geneva.