RBA Annual Conference – 2013 OTC Derivatives Reform: Netting and Networks Alexandra Heath, Gerard Kelly and Mark Manning[*]
1. Introduction
In the wake of the global financial crisis, member jurisdictions of the G20 have embarked upon an ambitious program of reforms to the structure and operation of financial markets. One key element of the reform program is to improve the management of counterparty risk and reduce interconnectedness in over-the-counter (OTC) derivative markets by encouraging greater use of centralised financial market infrastructure (Duffie, Li and Lubke 2010) and increasing the collateralisation of counterparty credit exposure. In accordance with the G20 commitments, new legislation was passed in Australia in December 2012, giving the Government the power to impose mandatory central clearing, trade reporting or platform-based execution requirements, if it is deemed necessary.
In promoting central clearing, policymakers aim to secure a number of benefits, including a reduction in exposure through multilateral netting and lower risk of contagion by decreasing interconnectedness between financial institutions. As the policy debate has progressed, however, a number of observers have identified important implementation challenges which, under certain conditions, could undermine the effectiveness of the reform proposals. As Pirrong (2012) argues, ‘although [the rules] may reduce some risks, they will simply relocate others, while creating some new ones’.
One concern that features prominently is that the ability of multilateral netting to materially reduce counterparty exposure will depend on the profile of market participants' trading activities and the degree of fragmentation in centralised clearing venues. If the benefits of existing cross-product netting are high and potentially offsetting exposures have to be cleared via different clearing venues, exposures of individual institutions and the system as a whole could actually increase in some circumstances (Duffie and Zhu 2011).
The effectiveness of netting and the size of outstanding net exposures will also have implications for the demand for high-quality liquid assets (HQLA). The transition to central clearing and the implementation of initial margin requirements where derivative trades remain non-centrally cleared will substantially increase the overall system demand for collateral-eligible assets, which may affect pricing, market structure and broader market functioning. Indeed, to the extent that the need to obtain collateral encourages the intermediation of HQLA between those with an excess and those with a shortfall (so-called, collateral transformation), new interconnections between financial institutions may emerge that could affect the resilience of the financial system in adverse conditions.
This paper presents a framework within which to consider these issues, building on the approaches in Jackson and Manning (2007), Duffie and Zhu (2011), and Cox, Garvin and Kelly (2013). The aim is to gain a better understanding of how different characteristics of agents, OTC derivative products and clearing arrangements may affect net exposures, collateral demand and financial stability, so as to identify where additional policy action may be necessary to ensure that the objectives of reforms are realised.
The paper extends previous work in this area in four important respects:
- it extends the ‘network’ by considering not only the derivative activities of dealers, but also those of agents in the periphery, which we term ‘investors’;
- it considers the implications of netting and market structure for both counterparty exposure and collateral requirements;
- in a stylised setting, it models the dynamic interaction between derivative exposure and other balance sheet items under alternative clearing arrangements, focusing on how price shocks are transmitted to balance sheets, and how these may trigger liquidity shortages and, in extremis, defaults; and
- it examines the potential impact of increased interconnectedness arising from investors acquiring collateral-eligible assets from dealer banks through collateral transformation arrangements, mapping out the dependencies and vulnerabilities associated with these arrangements.
The paper is structured, as follows. Section 2 provides some background on the policy rationale for an expansion in the scope of central clearing and on the implementation challenges that have been identified. Section 3 introduces the basic model framework, which focuses on the netting benefits in terms of exposure and demand for collateral under different clearing arrangements. The results of this section show that the netting benefits of moving from bilateral to central clearing arrangements disproportionately accrue to the ‘dealer’ institutions in the ‘core’ because they have a large number of counterparties and relatively balanced portfolios. This result is consistent with the existing literature. In contrast, investors in the periphery of the network have fewer counterparties and, under certain conditions, may have larger net exposure in a centrally cleared environment. Our results suggest that the case for central clearing is strongest for core institutions participating in large OTC derivative markets; the case for institutions in the periphery, which includes investors and smaller financial institutions, will depend on a range of factors.
Section 4 extends the basic model presented in Section 3 by considering the stability consequences of different clearing arrangements. To do this, we allow participants to obtain the collateral required to support their derivative activity by exchanging illiquid assets on their balance sheet. This analysis shows that there are trade-offs when risk is increasingly managed through collateralisation. On the one hand, financial stability improves due to a lower probability of insolvency arising from counterparty default when collateral coverage is higher. On the other hand, increased collateralisation leads to more encumbrance, so the risk of contagion rises because balance sheets are less liquid. Again, most of the financial stability benefits are likely to come from increasing the use of central clearing and collateralisation in the core and extending such requirements to peripheral institutions may, in some circumstances, have stability costs. We also show that potential stability costs arising from illiquidity increase if institutions in the periphery only have indirect access to HQLA via collateral transformation arrangements with the core. In light of the findings of this analysis, Section 5 considers the policy implications, and Section 6 concludes.
2. Background
At the Pittsburgh Summit, in September 2009, the G20 Leaders stated that: ‘All standardized OTC derivative contracts should be traded on exchanges or electronic platforms, where appropriate, and cleared through central counterparties by end-2012 at the latest’ (G20 2009, p 9). One of the core objectives of this decision is to mitigate systemic risk. This has been interpreted by the Financial Stability Board (FSB) to mean limiting the scope for contagion arising from interconnections between OTC derivative counterparties and the potential for crystallised losses to trigger procyclical increases in collateral calls on counterparties or the large-scale unwinding of exposures (FSB 2010).
Central clearing arrangements are expected to achieve this in a number of ways (Cecchetti, Gyntelberg and Hollanders 2009; Manning, Heath and Whitelaw 2010). First, central clearing generally provides greater netting efficiency, thereby minimising exposure. Second, central clearing is expected to reduce interconnections between institutions, thereby improving the robustness of OTC derivative markets to shocks and increasing financial stability. Third, central counterparties (CCPs) promote standardisation and support operational efficiencies in participants' position management and other back-office functions. Finally, CCPs are regulated against high and internationally consistent risk standards (CPSS-IOSCO 2012), and are able to manage defaults more effectively than bilateral counterparties.
Recognising that some products are not amenable to central clearing, perhaps because they are insufficiently standardised, policymakers have also developed new international principles for counterparty risk management where OTC derivative trades continue to be cleared on a bilateral basis (BCBS-IOSCO 2013). These principles propose harmonised requirements for both initial and variation margin between bilateral counterparties with the aim of replicating the risk management benefits of central clearing, and providing sufficient incentive to submit trades for central clearing wherever it is feasible to do so.
The rest of this section provides background on some of the matters relevant to the question of whether central clearing – and increased collateralisation where trades remain bilaterally cleared – is likely to be effective in achieving the G20's objective.
2.1 Netting efficiency – exposures
Contractual agreements between bilateral counterparties typically allow for bilateral netting of exposures across multiple products. In the event of a counterparty default, outstanding derivative contracts in all products covered by a given bilateral agreement would be terminated and netted against each other, either at agreed market values or at values reflecting any loss to the surviving party from replacing the trades (so-called close-out netting). Exposure in this context refers to potential loss in the event that one party defaults before its settlement obligations are met. Such losses arise when the market price of the contract moves adversely between the default event and the surviving counterparty's close-out of its exposure. This is known as replacement cost risk.
Under central clearing, netting occurs not only across all trades in the products accepted by the CCP, but also across all of a given agent's counterparties (multilateral netting). Duffie and Zhu (2011) make the point that whether netting across products or netting across counterparties minimises exposures is an empirical question and the outcome will differ across markets and individual participants. Relative to bilateral clearing, submitting trades to a CCP will be most effective in reducing aggregate exposures where agents have highly offsetting positions spread across a wide range of counterparties (Jackson and Manning 2007). These conditions are most likely to be satisfied for large dealers in OTC derivatives, who typically seek to hedge exposures that they assume through their trades with non-dealer banks, investors and corporates. Where agents trade with only a small number of counterparties, or there is less scope for netting because derivative exposures are positively correlated, multilateral netting will be less effective.
Duffie and Zhu (2011) establish that central clearing will only reduce exposures if both the number of agents and the size of centrally cleared exposures relative to those that remain bilaterally cleared are sufficiently large. Using data on OTC derivative positions across products, sourced from the Bank for International Settlements, the authors demonstrate that the central clearing of credit derivatives alone would be unlikely to satisfy the conditions for a reduction in total counterparty exposure, while interest rate swap positions may be sufficiently large to justify central clearing.
However, regulatory frictions or the privately chosen product scope of individual CCPs may leave participants unable to clear all related products through a single CCP, and hence unable to take full advantage of the scope for netting. For instance, some jurisdictions require that central clearing of domestic currency OTC derivative transactions take place through an onshore CCP, thereby preventing participants from taking advantage of netting opportunities across related products traded in different markets or currencies.[1]
2.2 Netting efficiency – collateral demand
Replacement cost risk is typically managed through the use of variation and initial margin. Variation margin is typically exchanged in cash at least daily to reflect mark-to-market price changes on participants' outstanding positions. Initial margin, on the other hand, is calibrated to cover, with a high probability, potential future exposure (or additional replacement cost losses that may occur) between the last variation margin payment and the close-out or replacement of a defaulting counterparty's trades. While variation margin is often already exchanged under existing bilateral arrangements, initial margin is generally not. New requirements to apply initial margin where trades are not centrally cleared will therefore constitute an important change in market practice (BCBS-IOSCO 2013).
Variation margin is calculated as the net change in the value of derivative positions due to observed price movements, with netting occurring across products and/or counterparties covered by a given bilateral or central clearing arrangement. Accordingly, variation margin is based on net exposures. In contrast, initial margin is calculated on the basis of future expected price movements and potentially offsetting price movements across products may not be fully taken into account. In CCPs, for instance, so-called ‘margin offsets’ are typically limited to distinct ‘families’ of products for which an empirically robust and economically justified correlation in price changes can be demonstrated, including in stressed circumstances. Therefore, even where the empirical covariance between price changes across products may imply significant scope for netting of exposures, the scope for collateral savings is likely to be much narrower.
Initial margin is usually paid in the form of HQLA, and so the netting efficiency of different clearing structures has direct implications for the demand for HQLA. There is increasing concern that the OTC derivative market reforms will lead to a significant increase in demand for HQLA as collateral to cover initial margin requirements because transactions covered by bilateral arrangements typically do not currently require initial margin (Heller and Vause (2011); IMF (2012); ISDA (2012); Sidanius and Zikes (2012); BCBS-IOSCO (2013); and Singh (2013), among others). To the extent that central clearing offers an effective way of reducing exposure arising from replacement cost risk, the increase in demand for HQLA may be mitigated. As noted by Tabb (2012), ‘… [t]he broader the range of open interest, the more opportunities a clearinghouse has to deliver collateral relief …’ However, ‘… for those who take on directional risk, or whose hedges do not fall into the same clearinghouse, the implications of the new collateral regime will be significant, especially if they use both cleared and un-cleared products’.
A quantitative impact study carried out by BCBS-IOSCO, summarised in BCBS-IOSCO (2013), estimates that applying initial margin requirements to those positions that do not transition to central clearing could lead to additional collateral demand of between €0.7 and €1.7 trillion, depending on the institutional scope of the requirements. Indeed, this is likely to add to other demands for HQLA arising from impending new liquidity requirements under Basel III and a general trend towards secured funding arrangements (Heath and Manning 2012; CGFS 2013).
The supply of HQLA is likely to be fixed in the short term. Accommodating an increase in collateral demand is therefore likely to involve significant adjustment in markets. This may have implications for the market structure and the network of exposures between financial institutions. For instance, it is likely that increased demand for HQLA will entail widespread portfolio reallocation, both as non-natural holders of HQLA shift a proportion of their balance sheets into such assets, and as existing holders reduce their holdings in response to an adjustment in relative prices. In some cases, including jurisdictions such as Australia with a low supply of HQLA, a policy response may be necessary to smooth the transition (see Heath and Manning (2012), Singh and Stella (2012) and Singh (2013)).
2.3 Network interconnectedness
A CCP becomes the buyer to every seller and the seller to every buyer in the markets it serves, thereby transforming a network of bilateral net exposures between participants into a single set of multilateral net exposures between the CCP and each market participant – a ‘star’ network (Figure 1). In this way, central clearing aims to reduce direct interconnectedness between counterparties, centralise default management, and address risks of contagion associated with the uncertainty about who is exposed to whom that exists in a bilateral network.
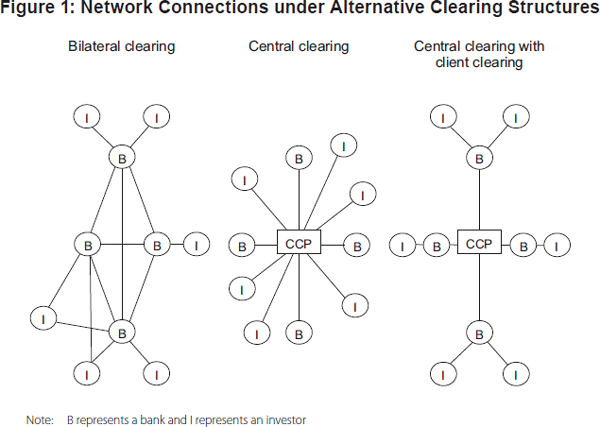
2.3.1 Client clearing
The extent to which central clearing simplifies the market structure and reduces the interconnectedness of the network will ultimately reflect the extent to which non-dealer banks, buy-side institutions or other end users of OTC derivatives transition to central clearing and whether they access CCPs as direct participants or indirectly via a clearing agent (client clearing). To the extent that they access central clearing indirectly, a new source of interconnectedness and dependence could emerge within the financial network.
In a client clearing structure, the clearing agent acts as a conduit to the CCP for its clients. The precise nature of the relationship between the client, the clearing agent and the CCP differs across jurisdictions, and across individual CCPs. In the agency model, which is common in the United States, the client maintains a direct contractual relationship with the CCP, but employs the clearing agent to act on its behalf in its day-to-day dealings with the CCP. Outside the United States, including in Australia, the alternative principal model predominates. In this model, the client has no direct contractual relationship with the CCP, only with the clearing agent. Accordingly, the CCP has no recourse to the client in the event of non-performance, and calls upon the clearing agent to guarantee its clients' performance. In either model, new interconnections are established between clearing agents and their clients (Figure 1).[2]
2.3.2 Collateral transformation
Increasing collateral demand may also increase interconnections in the OTC derivative network if access to HQLA is not evenly distributed. Of particular interest is collateral transformation, whereby an intermediary lends HQLA against less-liquid securities in return for a fee. Collateral transformation is in its infancy, but is widely expected to accelerate as the OTC derivative market reforms are implemented globally (Ellis 2012; ESRB 2012; IMF 2012).
Under such an arrangement, the collateral transformation provider would make HQLA available to an investor to meet a collateral requirement imposed by a central or bilateral counterparty, taking security over less-liquid assets posted by the investor. The clearing agent would either source HQLA from its own inventory or borrow them from another market participant in the repo market, for example. The collateral transformation provider would require that the investor post a higher value of less-liquid assets than the value of HQLA provided (a so-called ‘haircut’) to protect against a possible adverse change in the value of the less-liquid assets should the investor default.
It is generally acknowledged that, in the face of increasing collateral demands, there are efficiencies to be gained from the emergence of collateral transformation services. These services allow those with a shortfall of HQLA to meet their collateral requirements as they arise, rather than having to maintain these assets on their balance sheet. Other things being equal, such reallocation of portfolios would give rise to a steady-state increase in credit spreads and a concomitant decline in credit availability.
It is also recognised, however, that collateral transformation will be a source of new exposures and interconnections, taking the market further from the simple ‘star’ network that the OTC derivatives reform agenda originally sought to establish. Among the risks that have been highlighted in the policy debate so far, the potential funding risk for those relying on collateral transformation has been emphasised. In particular, collateral transformation transactions are typically of shorter maturity than the underlying OTC derivative transactions that they support. This introduces a rollover risk, which could crystallise in a number of ways: for example, an idiosyncratic shock to the collateral transformation provider; a tightening of conditions in the wider securities market; or a sharp decline in the value of the less-liquid assets posted as collateral.[3] The underlying market conditions and the responses of both the collateral transformation provider and the customer in such circumstances will determine the extent to which stress is spread more widely through the network.[4]
3. Netting under Alternative Clearing Structures
To characterise the way in which alternative clearing structures affect market participants' exposures to each other and their collateral implications, we use a relatively straightforward model that extends the Duffie and Zhu (2011) framework in two dimensions.
First, rather than assume that all participants are equal in size and trade with all the other participants in the market, which is consistent with the description of the core of an interbank or interdealer market, we add a layer of participants that trade with core institutions, but do not trade with each other. Several studies, including Upper and Worms (2004), Bech and Atalay (2010), Craig and von Peter (2010), and Markose (2012), have shown that this ‘core-periphery’ set-up is a more realistic and complete description of interbank and derivative markets. Babus (2011) shows that when collateral is costly and there are information frictions, a core of intermediary institutions can endogenously form to facilitate more efficient uncollateralised trading within long-term counterparty relationships.
The core of OTC derivative markets is arguably made of up of around 16 global banks that conduct most of their business in large financial centres such as London and New York, but also connect to more peripheral financial institutions that operate in regional financial centres. Since a large proportion of peripheral institutions' OTC derivative transactions are designed to hedge concentrated interest rate and currency risk, they are often highly directional and the logical counterparties to these transactions are large global banks. Extending the framework to include peripheral institutions allows us to consider the implications of different clearing arrangements for market participants such as end users of OTC derivatives and smaller, more domestically oriented investors and banks.
Second, we focus on the collateral implications of different market structures, rather than only the net exposures. This is important because the aggregate demand for HQLA to be posted as collateral to meet initial margin requirements may not have a linear relationship with those exposures. In particular, while variation margin payments reflect the impact of the single net price change on a portfolio of positions across all products held with a bilateral counterparty or CCP, initial margin requirements are typically calculated independently by product class, with only limited scope for cross-product offsets (see Section 2.2). As a result, the demand for HQLA to meet initial margin requirements will be quantitatively much more important than the demand arising from variation margin payments. Another consideration is that demand for collateral to meet initial margin is calculated at the beginning of a transaction and must be available in the event of a default, for example in a segregated trustee account. This reduces the velocity of collateral and increases the amount of collateral required to support a given level of activity.[5] In contrast, once variation margin is paid, typically in cash, the receiver is free to reuse the funds.
3.1 The model
The key elements of the basic model used in this section are the agents, the derivative products and the clearing arrangements. Our model is highly stylised and in the baseline case we do not attempt to calibrate the parameter values to match attributes of the real world accurately. In Section 3.4, however, we examine the sensitivity of our results to the choice of parameter values. The model is developed further in Section 4 to examine the dynamic response of the network to price shocks and highlight potential channels for contagion and financial instability.
3.1.1 Agents
We assume that the financial system has B banks that make up the core and I investors that make up the periphery. The banks in the core may be thought of as large dealers, while the investors in the periphery may be thought of as buy-side institutions. In the baseline case, we assume that B = 10 and I = 30.
3.1.2 Derivative products and positions
The net position between agent i and agent j in product
d is denoted
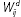 . A positive value
indicates that i has a ‘long’ position with j
in asset class d, while a negative value indicates a ‘short’
position. Accordingly,
. A positive value
indicates that i has a ‘long’ position with j
in asset class d, while a negative value indicates a ‘short’
position. Accordingly,
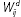 =0 and
=0 and
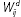 =−
=−
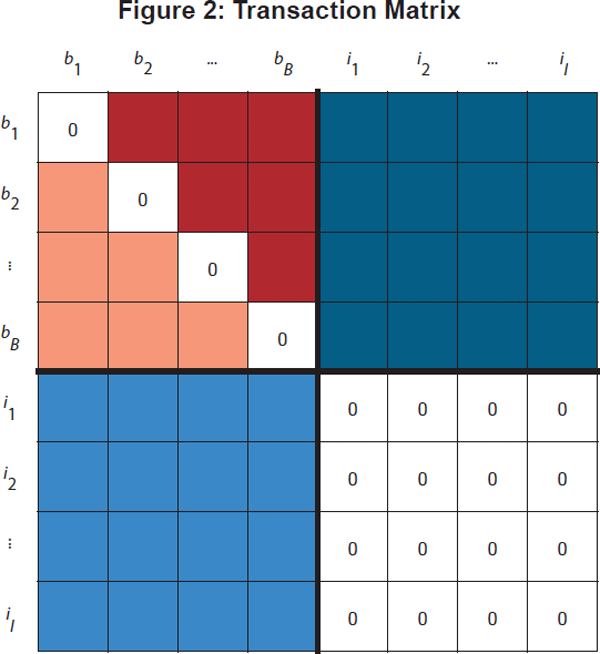
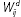 . All transactions
are contracted on a bilateral basis. The core is characterised as a dense network
of banks that trade with all the other banks in the core (the red block in
the transaction matrix in Figure 2). Investors transact only with banks
(the blue block) and not with each other.
. All transactions
are contracted on a bilateral basis. The core is characterised as a dense network
of banks that trade with all the other banks in the core (the red block in
the transaction matrix in Figure 2). Investors transact only with banks
(the blue block) and not with each other.
In the baseline case, we assume that there are two classes of derivative product,
and that net derivative positions,
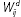 , are independent
across i and j
and across products. Derivative positions
, are independent
across i and j
and across products. Derivative positions
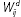 are randomly
assigned according to one of two bivariate normal distributions: N(0, ΩPB)
for positions between banks; and N(0, ΩPi) for positions
between banks and investors.
are randomly
assigned according to one of two bivariate normal distributions: N(0, ΩPB)
for positions between banks; and N(0, ΩPi) for positions
between banks and investors.
We define xd as the share of a bank's positions in product d
with other banks, and nd as the total notional value of
each bank's positions in product d. In the baseline case, the
expected total notional outstanding held by each bank in each of the two derivatives
products is normalised at 1. This implies that
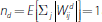 and
that n1 = n2 = 1. We also assume
that half of these positions are held against other banks and half against
investors, that is x1 = x2 = 0.5. These assumptions
pin down the variance-covariance matrix of positions as:
and
that n1 = n2 = 1. We also assume
that half of these positions are held against other banks and half against
investors, that is x1 = x2 = 0.5. These assumptions
pin down the variance-covariance matrix of positions as:
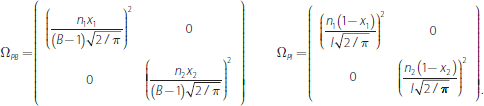
The matrix ΩR represents the covariance matrix for price movements (or returns) in the two derivative products. In the baseline case, we assume that there is no covariance between price movements (but relax this assumption in Section 3.4.2):
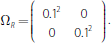
3.1.3 Clearing arrangements
We examine exposures and collateral demands under four alternative clearing arrangements, where:
- both products are bilaterally cleared (‘bilateral’)
- the core centrally clears both products with a single CCP, while the periphery bilaterally clears both products (‘split clearing’)
- one product is bilaterally cleared and one product is centrally cleared (‘mixed clearing’)
-
both products are centrally cleared with:
– each product cleared via a different CCP (‘separate CCPs’)
– a single CCP (‘single CCP’).
Under the centrally cleared arrangements, each bank and investor is assumed to access the CCP directly. We relax this assumption in Section 4.3, where we examine interdependencies introduced by client clearing and collateral transformation.
3.2 Exposures
We start by comparing the exposures generated under each clearing arrangement. Following
Duffie and
Zhu (2011), exposure is defined as expected loss given default, calculated
in terms of the expected change in mark-to-market valuations. This is also
the variation margin payment that would have been received had the counterparty
not defaulted. If we define ΔPd
as the change in the price of product d, then the variation margin
payment owing in respect of product d is given by
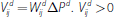 denotes that
i receives a variation margin payment from j, while
denotes that
i receives a variation margin payment from j, while
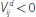 denotes that
i pays variation margin to j.
denotes that
i pays variation margin to j.
Given a transaction matrix and the covariance matrix of price movements for each derivative product, exposures for each agent will differ across clearing structures according to the netting properties of the structure. In particular:
-
When both products are bilaterally cleared, exposures are netted across products,
between each pair of counterparties. Note that the transaction matrix described
in Figure 2 is defined in terms of net bilateral positions, so there is no
scope for further netting of individual transactions in a given product executed
between a given pair of agents. Under these circumstances, the exposure of
agent i is given by:
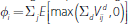 .
.
-
When the core is centrally cleared and the periphery is bilaterally cleared, the
exposures of these two groups are given, respectively, by:
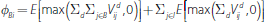 and
and
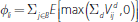 .
.
-
When one product, d1, is bilaterally cleared and the other, d2,
is centrally cleared, exposures in the centrally cleared product are subject
to multilateral netting across all participants in the CCP, while exposures
in the bilaterally cleared product are bilaterally netted between each pair
of counterparties. Under this hybrid model, the exposure of agent i
is given by
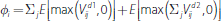 .
.
-
When the two products are centrally cleared by separate CCPs, exposures in each product
are multilaterally netted across all participants of each CCP separately.
The exposure of agent i is then given by:
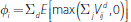 .
.
-
When both products are centrally cleared by a single CCP, exposures are netted multilaterally
across all products and all participants of the CCP. Under these circumstances,
the exposure of agent i is given by:
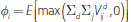 .
.
Table 1 presents exposure metrics for the baseline model under each clearing structure based on a Monte Carlo simulation with 300000 iterations. The table separately identifies exposures for each class of agent, including CCPs. In the final column, agents' and the central counterparties' exposures are summed to give total system exposure.
| Clearing arrangement |
Banks | Investors | All agents |
CCPs | System exposure |
|---|---|---|---|---|---|
| Bilateral | 0.63 | 0.31 | 0.94 | na | 0.94 |
| Split clearing | 0.44 | 0.31 | 0.73 | 0.13 | 0.89 |
| Mixed clearing | 0.47 | 0.26 | 0.73 | 0.14 | 0.87 |
| Separate CCPs | 0.15 | 0.13 | 0.28 | 0.28 | 0.56 |
| Single CCP | 0.12 | 0.10 | 0.22 | 0.22 | 0.44 |
The differences in the scope for netting give rise to differences in exposure outcomes across clearing structures in the baseline model. Consistent with Duffie and Zhu (2011), a single CCP offers the most netting-efficient solution. The system exposure with a single CCP clearing both products is less than half that in the bilateral structure. If only one product migrates to central clearing, however, the reduction in exposure relative to the pure bilateral structure is relatively limited. This reflects that, while agents can take advantage of multilateral netting for one of the products, the scope to net across products is lost.
The calculations in Table 1 assume there is a zero correlation between prices of the two derivative products. As we show in Section 3.4.2, the higher the (absolute) price correlation across products, the more valuable cross-product netting becomes and therefore the reduction in exposures from migrating one product to central clearing becomes smaller. This again accords with the conclusion in Duffie and Zhu (2011) that centrally clearing just one product may increase exposures. Also, a higher correlation in prices will increase the difference between system-wide exposures under a single CCP and separate CCPs.
Although the size of aggregate exposure falls moving from bilateral arrangements to a single CCP, the distribution of exposures shifts from being largely borne by banks in the core of the system to the CCP. This is consistent with the objective of the regulatory changes, which is to reduce risk in the system by reducing exposures and shifting risk to institutions that are considered to be in a better position to manage the risk; in this case, CCPs. However, the table also shows that, due to the greater scope for multilateral netting, banks in the core of the network benefit disproportionately relative to the investors in the periphery.
The split clearing structure allows us to examine further the relative importance of collateralisation and central clearing for core and peripheral institutions, and for the system as a whole. The second row of Table 1 reveals that, at least for the baseline case in which half of banks' trades are with investors, moving from bilateral to central clearing of trades within the core alone leads to a material reduction in banks' exposures. Investors' exposures, of course, remain unchanged. Total system exposure in the split clearing case remains significantly higher than when both products are centrally cleared. However, to the extent that interbank exposures are more systemically important – perhaps due to their higher concentration or greater propensity to trigger contagion in the event of a default in stressed circumstances – the ‘effective’ systemic risk reduction under split clearing may be greater than the expected loss captured by the total system exposure metric would imply.
3.3 Collateral demand
The demand for collateral to cover initial margin payments will be a non-linear function of counterparty exposures and the variances of price movements, which determine margin rates. The margin rate, m, is set to achieve a minimum level of coverage of price movements. This calculation may be based on the price distribution of an individual product (product-based margining) or of a portfolio margining.
3.3.1 Product-based margining
Unlike the calculation of variation margin, which is based on outstanding positions and observed price movements across all products covered by the counterparty relationship, initial margin calculations typically allow for only limited netting across products. While some margining methodologies applied by CCPs, such as CME SPAN, allow for some cross-product offsets – known as ‘inter-commodity offsets’ – these are typically applied only where there is a clear, empirically and theoretically robust correlation between the products in question. Initial margining proposals for non-centrally cleared derivatives equally allow very little scope for cross-product offsets in calculating margin requirements (BCBS-IOSCO 2013).
In the case of product-based margining, we assume that no cross-product offsets are
applied, and that target collateral coverage for each agent is 99 per cent
of single-tailed price movements for each product, consistent with international
standards for CCPs (CPSS-IOSCO 2012). Under bilateral clearing, the collateral
required to cover initial margin payments from agent i to agent j
for product d is then given by
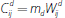 .[6]
Since, with product-based margining, long and short positions in different products
are not netted for the purposes of initial margining,
.[6]
Since, with product-based margining, long and short positions in different products
are not netted for the purposes of initial margining,
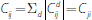 , and the collateral
requirement for agent
i will be Ci + Σj
Cij. Similarly, for a CCP, the total amount of collateral
required from participant i is
, and the collateral
requirement for agent
i will be Ci + Σj
Cij. Similarly, for a CCP, the total amount of collateral
required from participant i is
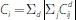 , which is the
same whether there is a single CCP for all products, or a separate CCP for
each product.
, which is the
same whether there is a single CCP for all products, or a separate CCP for
each product.
Table 2 reveals how the application of the product-based margining methodology translates to collateral demand under each clearing structure. Although relative collateral demands in Table 2 are qualitatively consistent with the exposures in Table 1, the relative magnitude of collateral demand under the bilateral structure with product-based margining is striking. This reflects that any observed cross-product netting is ignored for margining purposes. Bilateral clearing is therefore by far the most ‘costly’ market structure in terms of collateral demand and even centrally clearing only one product can give rise to material collateral savings. Indeed, while Table 1 reveals little difference between investors' exposures in the mixed clearing and split clearing cases, collateral demand is significantly higher in the split clearing case when cross-product netting is not reflected in margin calculations. Note also that since agents derive no benefit from pooling exposures with a single CCP when margin is calculated on a product-by-product basis, there is no difference in collateral demand between the single CCP and separate CCP structures. As before, although all agents experience a decline in their collateral needs, the banks in the core benefit disproportionately.
| Clearing arrangement | Banks | Investors | All agents |
|---|---|---|---|
| Bilateral | 5.15 | 2.58 | 7.73 |
| Split clearing | 3.43 | 2.58 | 6.01 |
| Mixed clearing | 3.07 | 1.70 | 4.76 |
| CCP | 0.99 | 0.82 | 1.80 |
3.3.2 Portfolio margining
While full portfolio margining is not typically observed, except within product classes, it is instructive to consider full portfolio margining as a lower bound for collateral demand. Under this methodology, initial margin is based on the potential future exposure on a portfolio of products, rather than on each product individually. In this exercise we assume that the margin rate is calibrated to cover 99 per cent of price movements across the entire portfolio, which is consistent with expectations for portfolio-level variation margin obligations calculated in Section 3.2.
Portfolio margining will only be relevant in cases where both products are cleared
bilaterally or are cleared centrally through a single CCP. In the case of bilateral
clearing, the collateral required for each agent in a bilateral relationship
under portfolio margining is given by
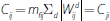 .[7]
In the case of central clearing, the collateral required of each participant
will be given by
.[7]
In the case of central clearing, the collateral required of each participant
will be given by
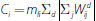 .[8]
.[8]
In general, portfolio margining materially reduces the amount of collateral required for initial margin (Table 3). The extent of the reduction will be affected by the covariance between the price movements of different asset classes and the weights of each asset class in the portfolio (see Section 3.4.2). A comparison of the collateral demands in Table 3 with those in Table 2 demonstrates that material collateral savings may be achieved if (prudent) cross-product netting is recognised in calibrating margin requirements.
| Clearing arrangement | Banks | Investors | All agents |
|---|---|---|---|
| Bilateral | 4.05 | 2.02 | 6.07 |
| Split clearing | 2.80 | 2.02 | 4.81 |
| Single CCP | 0.77 | 0.64 | 1. 41 |
3.4 Exposure and collateral demand: comparative static analysis
The results in Tables 1 to 3 are, of course, dependent on the baseline parameters chosen. To explore how exposure and collateral demand under each alternative clearing structure vary with product and agent characteristics, we conduct a number of experiments, individually varying key parameters of the baseline model. In particular we consider the effect on exposure and collateral demand of: varying the size of the core relative to the periphery (Section 3.4.1); varying the characteristics of derivative products (Section 3.4.2); and allowing a sub-section of the periphery to take directional derivative positions (Section 3.4.3).
3.4.1 Varying the size of the core relative to the periphery
One of the motivations for extending the Duffie and Zhu (2011) model is to understand how the presence of institutions in the periphery might affect conclusions around the costs and benefits of central clearing arrangements. To do this, we examine the effects on exposure and collateral demand of: varying the size of the core, while keeping the size of the periphery fixed; varying the size of the periphery, while keeping the size of the core fixed; and varying the share of notional amounts outstanding traded within the core.
Figure 3 summarises the effect of linearly increasing the number of banks in the core on total system exposure and total collateral demand relative to total notional outstanding, under each clearing structure, holding the total size of notional amounts outstanding fixed.[9] As expected, when derivatives are bilaterally cleared, varying the number of banks in the core has no effect on either relative exposure or relative collateral demand since, under this clearing structure, there is no scope for netting across counterparties. In contrast, in structures involving central clearing, exposures and collateral demand decline steadily as the number of banks in the core increases, though at a decreasing rate. This is intuitive: multilateral netting across counterparties is more valuable, the larger the number of counterparties (Jackson and Manning 2007). The left-hand panel of Figure 3 shows that for a small core, netting across products available in a bilateral clearing relationship may be more important than netting across counterparties. This is consistent with the findings in Duffie and Zhu (2011). This may also be true for collateral demand (the right-hand panel), depending on whether initial margin requirements are calculated on a product or portfolio basis.
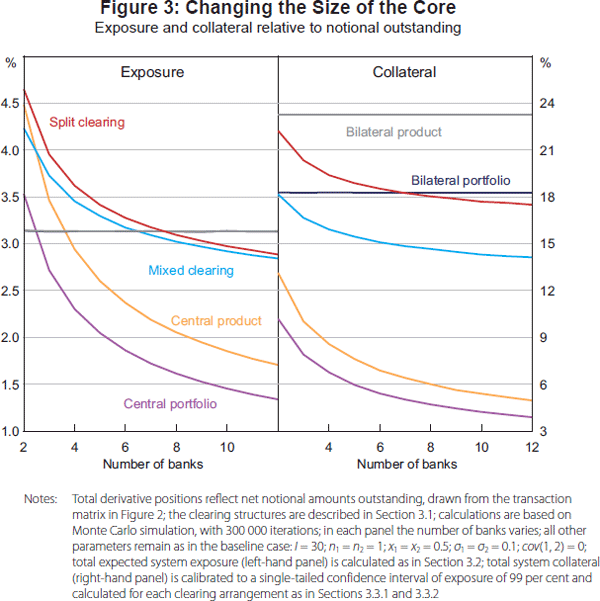
Figure 3 also reveals that, in the case of split clearing (for the baseline case in which half of the nominal value of each bank's trades is with the periphery), exposure falls to below that under full bilateral clearing as the number of banks increases. Further, split clearing always gives rise to higher exposure for these parameter values than the mixed case, though exposure always remains above that under full central clearing.
A similar picture emerges when we consider increasing the number of investors with a fixed number of banks in the core; there is a steady decline in both exposure and collateral demands in the arrangements involving central clearing, as multilateral netting opportunities increase. However, these benefits accrue only to the core (again, since investors do not trade with each other, they experience no change in the scope for multilateral netting of their exposures).
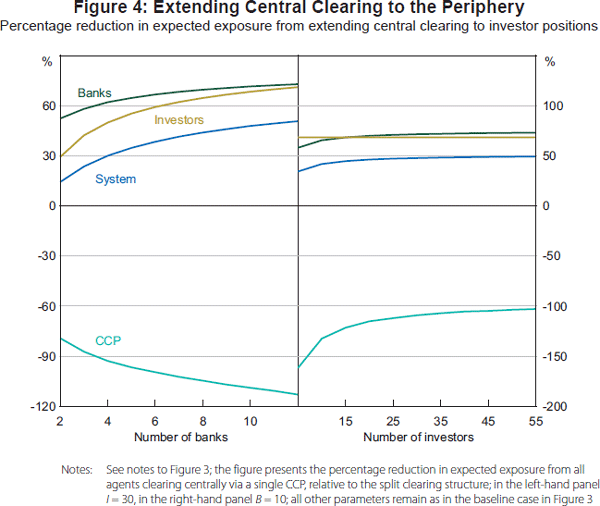
Figure 4 examines the implications of network structure by comparing the relative reduction in exposure for each agent type as central clearing (via a single CCP) is extended to the periphery. In the left-hand panel, changes in exposure are tracked as the number of banks in the core increases, and in the right-hand panel as the number of investors in the periphery increases. It is evident that when there are only few banks in the core, the benefits to investors from central clearing are relatively limited. Again, this reflects relatively less scope for multilateral netting. This is equivalent to investors trading only with a few dealers, which for many investor types is likely to accord with observed practice. As the number of core banks increases, however, the benefits to investors converge on those for banks, since the scope for multilateral netting increases. The right-hand panel, on the other hand, shows that investors' exposures remain unchanged as the number of investors changes (since investors are assumed not to trade with each other). Increasing the number of investors does, however, generate multilateral netting benefits for banks, and therefore there is a material reduction in exposure for the core.
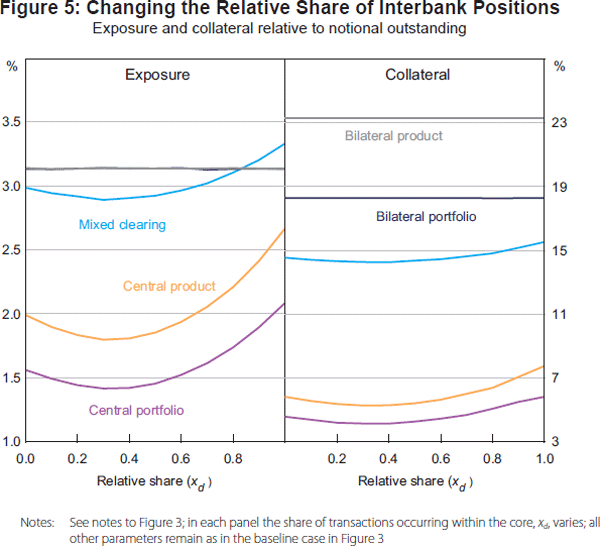
Finally, it is also instructive to consider how netting efficiency and collateral demand change when the share of OTC derivative transactions occurring within the core varies (Figure 5). As the degree of concentration of transactions increases within a relatively small core of 10 banks, the relative benefit of central clearing versus bilateral clearing diminishes. This reflects that with a smaller share of exposure outside the core, multilateral netting benefits associated with exposure to the periphery decline.
3.4.2 Varying the characteristics of derivative products
The netting efficiencies of different clearing structures also depend on the characteristics of the derivative products that are traded. To examine this, we vary the relative size of the two derivative products and the relative volatility of their prices, and allow their prices to be correlated. In a final experiment, we also allow the number of products to vary.
In the first experiment, we scale up the size of positions in one derivative product incrementally and consider the implications for total system exposure and collateral demand (relative to total system notional amounts outstanding) across the different clearing arrangements. In the mixed clearing case, we increase the size of the bilaterally cleared derivative. Two observations in Figure 6 are particularly striking:
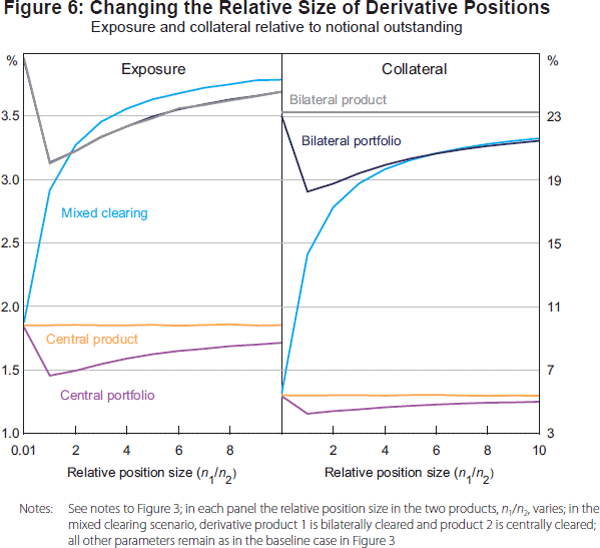
- First, increasing the relative size of positions in the bilaterally cleared derivative product materially increases both exposure and collateral demand in the mixed clearing structure. This is consistent with Duffie and Zhu (2011). In effect, the multilateral netting benefits from centrally clearing one product diminish as the size of positions in the bilaterally cleared product increase, and the characteristics of the portfolio converge to those under pure bilateral clearing. Indeed, at some point, the ‘un-netting’ effects result in slightly larger exposure in the mixed clearing case.
- Second, exposure under the single CCP structure gradually approaches that under the structure with separate CCPs. The interpretation of this result is similar: as the size of one product increases relative to the other, the benefits of netting across products begin to diminish. This also holds for collateral: in the structures with portfolio margining, collateral demand starts to converge on that with product-based margining.
In the second set of experiments, we allow the volatility of derivative prices to vary and the correlation between them to be non-zero. As one would expect, increasing the volatility of one derivative product while the other is held fixed leads to an almost linear increase in exposure and collateral demand. The increase in exposure is steeper for the bilateral clearing structures, due to the diminishing scope for any netting as volatility in the price of one product dominates price changes in the portfolio. Similarly, as the benefit of cross-product netting diminishes, collateral demand under product and portfolio margining in each of the bilateral and centrally cleared structures rise at the same linear rate.
As foreshadowed in Section 3.3, allowing the covariance between derivative price changes to be non-zero has significant implications for exposure and collateral demand. In particular, for those clearing arrangements that allow for cross-product netting (i.e. bilateral clearing and clearing via a single CCP, left-hand panel Figure 7), exposure falls when derivative price changes either become more positively or more negatively correlated. A similar hump-shaped profile is also evident for collateral demand when correlations between derivative price changes are taken into account in setting margin requirements.
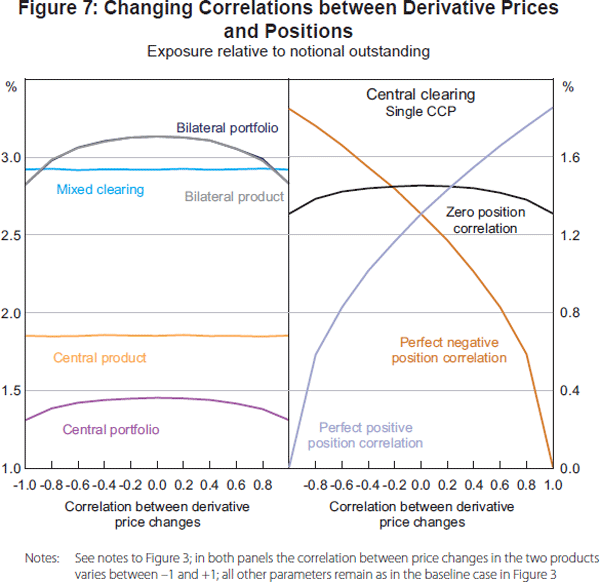
In the baseline model, we have assumed that there is no correlation between participants' positions in the two derivative products. One would expect that as the correlation between these positions increases, the impact of increasing the (absolute) correlation between prices on exposure would also increase. The right-hand panel of Figure 7 illustrates this point for the case of central clearing with a single CCP. As positions become more negatively (positively) correlated, and prices become more positively (negatively) correlated, exposure tends to zero because these combinations constitute fully hedged positions. The highest exposure occurs when prices and positions both have correlations of either +1 or −1.
Finally, we consider the implications of changing the number of derivative products. As might be expected, and consistent with Duffie and Zhu (2011), increasing the number of products increases the value of cross-product netting. Accordingly, as the number of products increases, bilateral clearing and central clearing via a single CCP begin to look proportionally better than fragmented clearing arrangements.
3.4.3 Directionality
In the baseline model, we have assumed that the net positions between institutions in product d are independently drawn from a normal distribution with mean zero. In general, this is likely to be a good first approximation for net positions between banks in the core of the network, since these are large global banks that act as intermediaries to the periphery and much of this ‘interdealer’ activity is intended to distribute risk efficiently throughout the system.
For the periphery, however, it is quite likely that many institutions' OTC derivative positions are designed to hedge exposure arising from other activities. For example, a pension fund may seek to hedge interest rate or currency risk in its investment portfolio; a peripheral bank may seek to hedge the currency risk associated with offshore funding, or the mismatch between the interest rate exposure of its assets and liabilities; and a mining company may use derivatives to hedge its exposure to a change in commodity prices. Furthermore, there may be clusters of institutions in the periphery with very similar net OTC derivative positions, with their natural counterparties often large global banks who subsequently lay off any residual exposure by trading with other banks in the core. In this subsection, we consider how exposure and the demand for collateral change under different clearing arrangements if a subset of financial institutions in the periphery (investors in the terminology of the model) has directional positions.
To do this, we assume that a subset of investors in the periphery draw their positions from a half normal distribution with mean zero. The remaining investors draw their positions from the normal distribution described in Section 3.1. As the directionality of the periphery increases, modelled here as an increase in size of the directional subset, the scope for multilateral netting diminishes. Netting across products may, in such circumstances, be a more important driver of exposure – and hence collateral demand – than netting across counterparties.
This is confirmed by Figure 8, which reveals that as the directionality of the periphery increases, the benefit of multilateral netting in the structures involving central clearing declines and exposure eventually rises to be above that in the bilateral and mixed clearing structures. This may seem surprising, particularly since central clearing via a single CCP allows netting across both counterparties and products. The increase in centrally cleared exposure above that under bilateral clearing can, however, be explained by the fact that system exposure is the sum of exposures to all agent types, including CCPs; the net exposures of each agent type under central clearing with a single CCP remain below those under bilateral clearing. Since the CCP does not post collateral, higher exposure under central clearing relative to bilateral clearing does not translate to higher collateral demand.
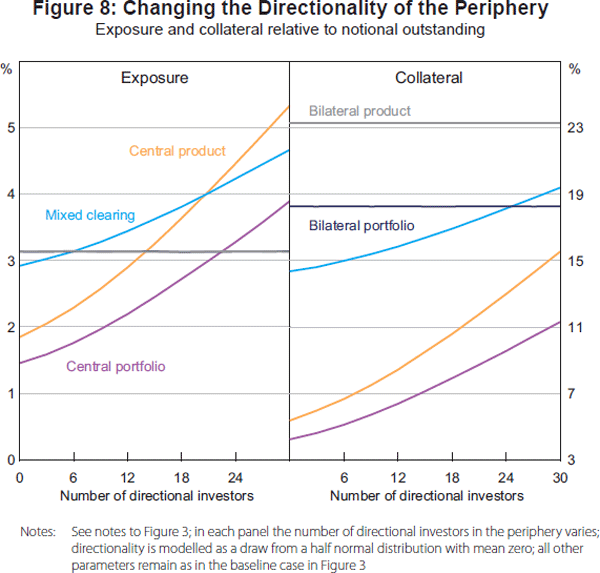
The fact that exposure and collateral demand are independent of the number of directional investors in the bilaterally cleared arrangements is a function of the assumption that there is zero correlation between derivative prices. If the prices of the two derivative products were correlated, there would be greater scope for cross-product netting, especially if the positions were negatively correlated (see Section 3.4.2). Opportunities to net across products would further increase the relative advantage of bilateral over centrally cleared arrangements.
These results highlight the importance of considering the size and distribution of positions in the periphery when analysing the costs and benefits of alternative clearing structures. In some cases, the cross-product netting available under bilateral arrangements may be more valuable than the cross-counterparty netting under central clearing arrangements, and lead to lower exposure. It is also the case that because the core benefits disproportionately from multilateral netting, the costs and benefits of different arrangements may differ across agent types.
3.5 Summary
The results in this section confirm that central clearing generally delivers lower exposure and collateral demand. However, the magnitude of the benefits from central clearing, and to whom they accrue, will depend on the particular characteristics of agents and the products they trade. In particular:
- Given the more limited multilateral netting benefits available to investors, the exposure reduction associated with central clearing accrues disproportionately to the core. When the notional value of trades executed with the periphery is low relative to that executed within the core, the effective number of core counterparties with which investors typically trade is small. When investors' trades are highly directional, the relative benefits to investors from central clearing are further reduced.
- Netting across products (which is available under bilateral clearing, or clearing via a single CCP) may, in some circumstances, deliver greater benefits than netting across counterparties, particularly when cross-product offsets are taken into account in calibrating initial margin requirements. Such netting will be more valuable the higher are the absolute correlations between positions and/or prices in the two derivative products. In such circumstances, bilateral clearing may appear more favourable than fragmented central clearing or mixed clearing arrangements.
4. Networks under Alternative Clearing Structures
One of the main arguments for moving to central clearing is that it offers netting benefits relative to bilateral clearing. These benefits accrue to individual institutions and, as the analysis in Section 3 has highlighted, they are likely to be higher for institutions in the core of the financial network. Another argument for moving to central clearing is that it will result in a more robust network than one comprising only bilateral arrangements. Recent literature has suggested that in interbank or interdealer financial networks, central clearing is robust to ‘random’ defaults, but may be fragile in the face of multiple correlated defaults (Gai, Haldane and Kapadia 2011). An alternative characterisation of this is that CCPs lower the risk that isolated (extreme but plausible) defaults have systemic consequences, but concentrate the consequences and management of multiple defaults within one institution. A countervailing benefit of a CCP, however, is that its central position should allow it to manage the liquidation of defaulters' outstanding positions more efficiently than could a network of bilateral counterparties. In this section, we look at the financial stability consequences of different clearing arrangements in our core-periphery model by considering the size and composition of agents' balance sheets, and examining the dynamic behaviour of the network in response to changes in asset prices.
For each institution we specify a balance sheet which comprises only illiquid assets (IA) funded by either debt liabilities or equity. Banks and investors are able to convert IA into HQLA to meet the collateral requirements related to their OTC derivative exposure. We allow IA prices to change relative to those for HQLA and examine how increasing the level of collateralisation under the alternative clearing arrangements affects exposure, collateral demand and vulnerability to default.
In our model, default can occur either because cumulative losses wipe out the equity of a bank (which we term insolvency), or because a bank or investor has insufficient unencumbered assets on its balance sheet to raise the HQLA required for a margin payment (which we term illiquidity). The dynamic nature of the exercise allows us to examine how the default of one institution affects the stability of the financial system as a whole under different clearing arrangements.
After discussing the main results in Section 4.2, we extend the model further in Section 4.3, by assuming that institutions in the periphery rely on institutions in the core to source the HQLA they need to meet their collateral obligations; that is, they rely on collateral transformation. This allows us to isolate a particular source of interconnectedness between the core and the periphery that may generate additional liquidity pressures for individual institutions and become an additional channel for contagion between institutions. In Section 4.4, we look at the sensitivity of the results in the model with collateral transformation to different parameter values. Section 4.5 provides a short summary of the findings.
The model is highly stylised to ensure tractability in the simulation, and the parameters describing agents' activities and balance sheets are not sufficient to replicate the observed complexity of agents' exposures. For instance, given the simple structure of the balance sheets we use, all observed asset encumbrance is attributed to meeting collateral requirements associated with derivative exposure. In a richer setting, with more types of assets and liabilities, OTC derivative positions could be modelled as the marginal source of encumbrance, and accordingly as an amplifier of stress rather than its proximate cause. Furthermore, parameter values in the baseline model exaggerate the economic significance of OTC derivative positions. This enables us to draw out key relationships, dependencies and interactions, and to demonstrate how derivative exposure and the arrangements used to manage counterparty risk may either amplify or mitigate the effect of asset price shocks.
4.1 The model
The dynamic model builds on the static model in three main ways:
- it includes stylised balance sheets that are specified for both banks and investors, allowing OTC derivative exposure and collateral demands to interact with other balance sheet components
- it allows for institutions in the network to default either due to illiquidity or insolvency, resulting in seizure of collateral and, in some circumstances, crystallisation of losses, with possible spill-over effects
- a Monte Carlo simulation is run, with 70,000 iterations, in accordance with a specified time line of events to examine how the system responds to balance sheet shocks under alternative clearing structures.
We assume participants in the network can hold two types of assets on their balance
sheets: HQLA and IA. HQLA are held solely to meet market participants'
collateral obligations. The price of IA in units of HQLA,
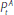 , varies exogenously
from one period to the next according to a random walk, with the percentage
change
, varies exogenously
from one period to the next according to a random walk, with the percentage
change
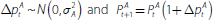 .[10]
It is assumed that the initial price
.[10]
It is assumed that the initial price
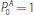 . In the baseline
case, the standard deviation of IA prices is assumed to be σA
= 0.05. Initially, both banks and investors are assumed only to have IA on
the asset side of their balance sheets.
. In the baseline
case, the standard deviation of IA prices is assumed to be σA
= 0.05. Initially, both banks and investors are assumed only to have IA on
the asset side of their balance sheets.
Assets may be funded by equity, K, or (unspecified) debt liabilities, L, which have a fixed price (relative to HQLA). Banks start with 5 per cent equity in the baseline model, whereas investors are assumed to be entirely funded by equity (consistent with investors representing buy-side institutions such as pension funds or collective investment schemes). Each period, the price of IA can move. This leads to changes in the value of assets that can only be accommodated by changes in the value of equity, given that, for banks, the value of other liabilities remains constant in HQLA terms, and investors only have equity liabilities. The initial size of banks' balance sheets is assumed to be one-tenth the expected total notional outstanding of their derivative positions (0.2), and twice the size of investors' balance sheets (0.1).
| Each bank | Each investor | ||
|---|---|---|---|
| Assets | Equity and liabilities |
Assets | Equity and liabilities |
| IA : 100 | L: 100–k | IA: 100 | K: 100 |
| K: k | |||
Derivative positions do not appear on the balance sheet, but once positions are established,
HQLA must be acquired to meet associated initial margin requirements. This
has consequences for balance sheets. Initially, institutions in the network
are assumed to have access to a Securities Market in which IA can be sold to
generate HQLA (and vice versa) at the asset price
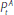 . We assume that
there are no shortages of HQLA in aggregate (CGFS 2013). The total amount of
HQLA required to cover the initial margin on participant i's derivative
transactions is the collateral position discussed in Section 3.
The HQLA pledged to either a central or bilateral counterparty to meet an initial
margin requirement appears as encumbered HQLA on the asset side of the balance
sheet, and the remainder of a bank's assets are IA. Derivative positions
are marked to market each period, which generates variation margin payments
in HQLA. These have further implications for balance sheets in subsequent rounds
of the simulation.
. We assume that
there are no shortages of HQLA in aggregate (CGFS 2013). The total amount of
HQLA required to cover the initial margin on participant i's derivative
transactions is the collateral position discussed in Section 3.
The HQLA pledged to either a central or bilateral counterparty to meet an initial
margin requirement appears as encumbered HQLA on the asset side of the balance
sheet, and the remainder of a bank's assets are IA. Derivative positions
are marked to market each period, which generates variation margin payments
in HQLA. These have further implications for balance sheets in subsequent rounds
of the simulation.
In the baseline scenario, we assume that balance sheets are around one-tenth the size of outstanding notional derivative positions. As noted, the combination of parameters chosen in the baseline model aims to highlight the underlying mechanisms more starkly than may be realistic. We go some way towards exploring the implications of our parameter choices in Section 4.3. However, there is scope for further work on this.
At t = 0, the transaction matrix is populated as in the model in Section 3.1. In each subsequent period, the following actions are described by the time line in Figure 9.
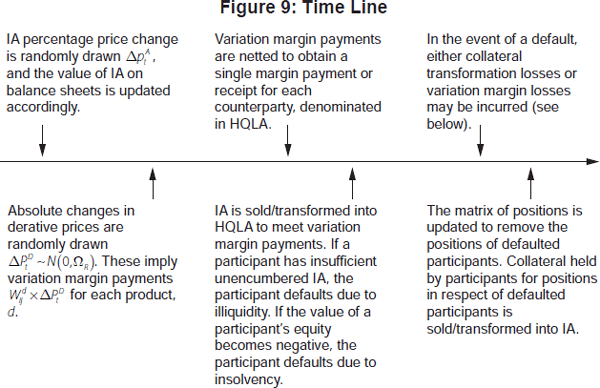
The baseline simulation runs for five periods. The larger the number of time periods, the greater the scope for losses and bank or investor defaults to occur. In particular, any depletion of unencumbered IA, for reasons including variation margin losses incurred or price changes, increases an agent's vulnerability to derivative price shocks in the next period.
Bank or investor defaults may arise in two ways in the model:
- Insolvency. Changes in asset prices and the payment or receipt of variation margin can expand or shrink the size of agents' balance sheets. Any change in the asset side of a balance sheet is necessarily balanced by an equivalent change in equity. Should an agent's equity be fully depleted, that agent is considered to have defaulted due to insolvency. Only a bank can become insolvent, however, since investors do not hold any non-equity liabilities.
- Illiquidity. To meet a variation margin call, a bank or investor must sell IA to purchase HQLA. This is done in the Securities Market. Should an agent be unable to meet a variation margin call due to insufficient unencumbered IA, that agent is considered to have defaulted due to illiquidity. There are three factors that can lead to a decline in unencumbered IA, and hence potential illiquidity: IA may be sold to generate HQLA to meet initial margin requirements on derivative positions established at t = 0; the value of IA may decline due to adverse IA price shocks; and holdings of IA may be depleted due to variation margin payments.
Should a bank or investor default, the surviving counterparty seeks to cover any unpaid variation margin owed using initial margin previously collected from that party. Should this be insufficient to cover the defaulting party's obligation, the shortfall is either subtracted from the surviving counterparty's IA (in the case of bilateral clearing), or subtracted in equal shares from the IA of all surviving participants of the CCP (in the case of central clearing). This is therefore another channel for contagion: changes to IA from ‘variation margin losses’ may cause other agents' IA or equity to become negative, in which case there would be further defaults, and further losses may arise.[11]
4.2 Collateral coverage and system stability
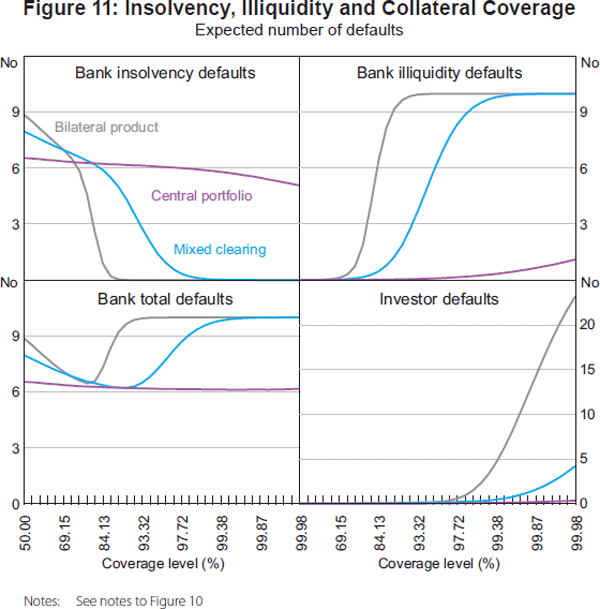
Figure 10 plots the expected number of bank defaults at differing levels of collateral coverage for three of the clearing arrangements under consideration: bilateral clearing with product-based margining, mixed clearing, and central clearing with portfolio margining.[12] Since losses arise in only one tail of the distribution for any agent (e.g. the default of a counterparty with a long position only gives rise to losses if the price has declined), 50 per cent coverage of the price distribution is achieved with zero collateral. The key metric of interest is the expected number of bank defaults.
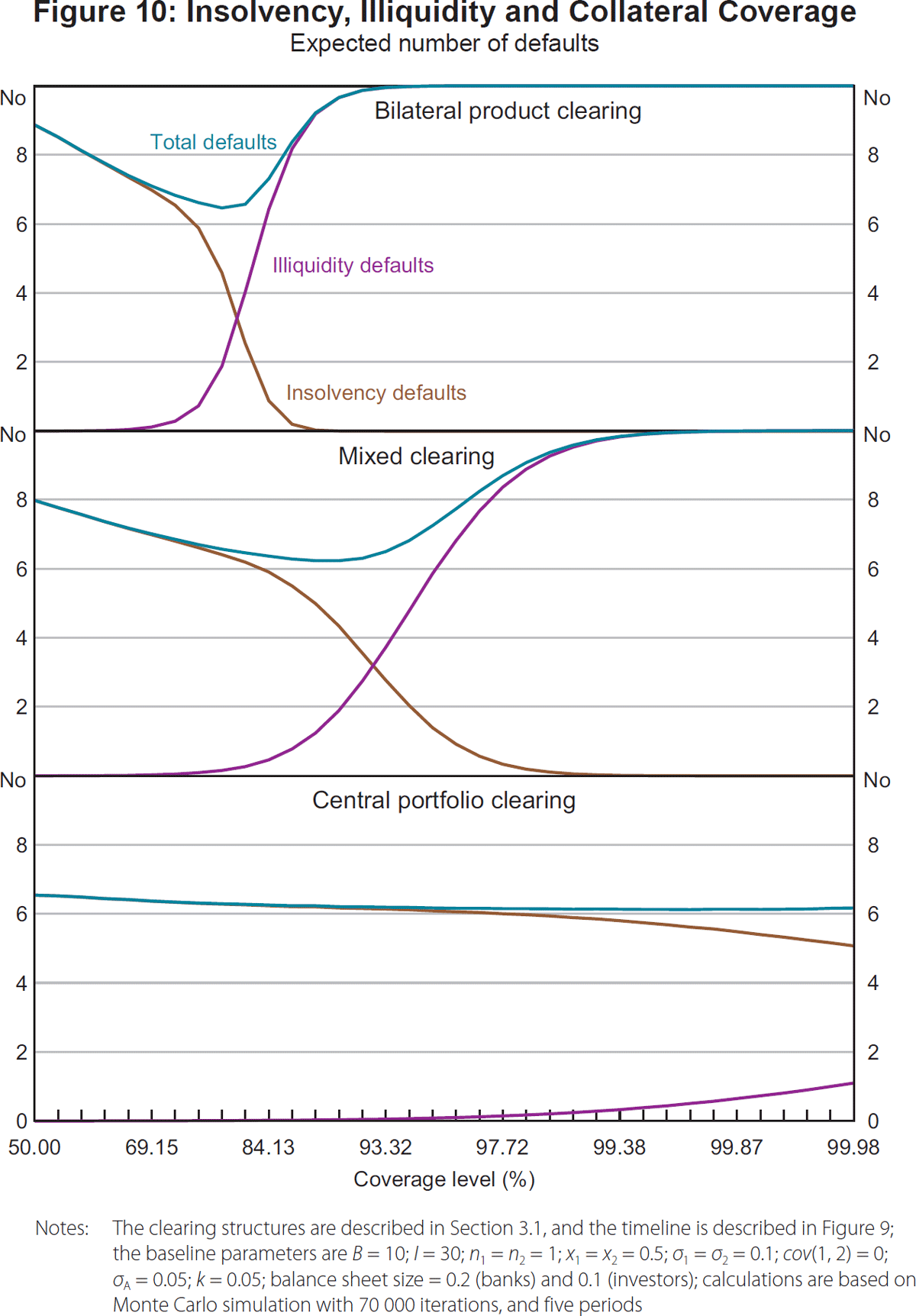
Consistent with its role in mitigating the losses associated with a counterparty default on an OTC derivative contract, increased collateral coverage is associated with a decline in the incidence of bank defaults due to insolvency.[13] This is depicted by the downward-sloping brown line in each plot.
However, at the same time, as collateral coverage increases, agents must encumber a larger share of their balance sheets, making them more vulnerable to asset price shocks and reducing their ability to access liquidity to meet future variation margin obligations. This vulnerability is reflected in an increase in the incidence of bank defaults due to illiquidity (the upward-sloping purple line in each plot). There is a level of collateral coverage at which the increase in defaults due to illiquidity exceeds the decrease in defaults due to insolvency, revealing a U-shaped relationship between total expected bank defaults and collateral coverage. That is, there will be an optimal level of collateral coverage which represents the best trade-off between insolvency and illiquidity.
There are notable differences across clearing arrangements in the slopes of the curves and the level of collateral coverage at which total expected bank defaults reaches a minimum. Consider first bilateral clearing with product margining (the first panel of Figure 10). As collateral increases from 50 per cent coverage, the incidence of bank defaults due to illiquidity increases at a faster rate than the decline in bank defaults due to insolvency, and rapidly exceeds the highest level of bank defaults due to insolvency. When central clearing of at least one product is introduced, the gradient of the curves flatten a little, resulting in an extended U-shaped ‘total defaults’ curve that reaches a minimum at a higher level of collateral coverage. With both products centrally cleared, the increase in bank defaults due to illiquidity and the decline in bank defaults due to insolvency as collateral coverage increases are less pronounced. The ‘total defaults’ curve does, however, attain a minimum at a very high level of coverage. The key driver of the difference in the slopes is the greater collateral efficiency of central clearing highlighted in Section 3.
Figure 11 summarises the results by separately identifying the source of default – that is, insolvency and illiquidity (top panels) – and plotting expected total bank and total investor defaults (bottom panels). The plot of total bank defaults, in particular, illustrates clearly how greater netting efficiency shifts optimal collateral coverage to the right and flattens the U-shaped relationship between bank defaults and collateral coverage. As noted in Section 4.1, investors cannot default due to insolvency because they are fully funded by equity and can therefore only default due to illiquidity. The incidence of investor defaults rises particularly sharply with collateral coverage in the clearing arrangements with low netting efficiency at coverage levels that exceed the optimum, but increases only marginally under central clearing.
4.3 Collateral transformation
Although we continue to assume that there is no shortage of HQLA in aggregate, we now adapt the model described in Section 4.1 to assume that, due to segmentation in markets and other frictions, access to HQLA is not evenly distributed (BCBS 2012). In particular, we assume that banks in the core retain their access to the (un-modelled) Securities Market to obtain HQLA, but that investors can only obtain HQLA by entering into a collateral transformation agreement with a core bank. This creates new interconnections between the core and periphery. This is likely to be an increasingly important feature of funding markets going forward, as described in Section 2.2.4.
We further assume that the bank that provides collateral transformation services to a given investor using central clearing does so in conjunction with client clearing services. In particular, each investor is assumed to access the CCP via a clearing agent, but with an individually segregated client account, such that no financial exposure is created between the investor and its clearing agent other than through the provision of collateral transformation. There is, however, an operational dependence associated with both client clearing and collateral transformation, since an investor's clearing agent may fail. We assume that client positions, collateral and collateral transformation transactions may be ‘ported’ – that is, transferred to a surviving bank – in the event that an investor's clearing agent defaults. If all banks default, there is no further scope for porting, at which point ‘the system’ defaults.
4.3.1 The adapted model
We introduce collateral transformation by assuming that each investor makes arrangements with a randomly selected bank to pledge a defined quantity of IA in exchange for HQLA. The bank, in turn, pledges the HQLA to the investor's counterparty (either a CCP or bilateral counterparty, depending on the clearing structure). The pledged IA remains on the investor's balance sheet, but appears as encumbered (IA*), while the HQLA pledged by the bank to the investor's counterparty appears as encumbered on the bank's balance sheet (HQLA*). Should the investor default on its obligation to its counterparty, the bank loses its pledged HQLA, but takes title over the investor's encumbered IA.
To manage the risk that the value of pledged IA changes, banks require that investors pledge a higher value of IA than the HQLA they loan in return. The difference between these values – the haircut, h – is designed to mitigate losses for a bank in the event that the price of IA falls relative to HQLA following the default of an investor. In the baseline case, h is assumed to be calibrated to cover 99 per cent of potential one-period IA price movements. That is, for investor i, with collateral requirements of Ci, the bank will have Ci of HQLA encumbered on its balance sheet, which has been posted to the CCP on behalf of the investor, and the investor will have (1+h)Ci of IA encumbered on its balance sheet.
| Each bank | Each investor | ||
|---|---|---|---|
| Assets | Equity and liabilities |
Assets | Equity and liabilities |
| IA: 100 – Ci | L: 100–k | IA: 100 – (1+h) Ci | K: 100 |
| HQLA*: Ci | K: k | IA*: (1+h) Ci | |
Should a bank default during the period, investors with which it has a collateral
transformation relationship will be assigned (randomly) to one of the surviving
banks.[14]
In the event of an investor default, the bank loses the Ci
in HQLA that it had encumbered on the investor's behalf and receives the
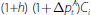 in IA that the
investor had encumbered on its balance sheet. If the price falls by a sufficiently
large amount that it exceeds the haircut on the exposure,
in IA that the
investor had encumbered on its balance sheet. If the price falls by a sufficiently
large amount that it exceeds the haircut on the exposure,
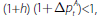 , the bank faces
a ‘collateral transformation loss’, which is recorded as a reduction
in HQLA and a corresponding reduction in equity.
, the bank faces
a ‘collateral transformation loss’, which is recorded as a reduction
in HQLA and a corresponding reduction in equity.
4.3.2 Results from the adapted model
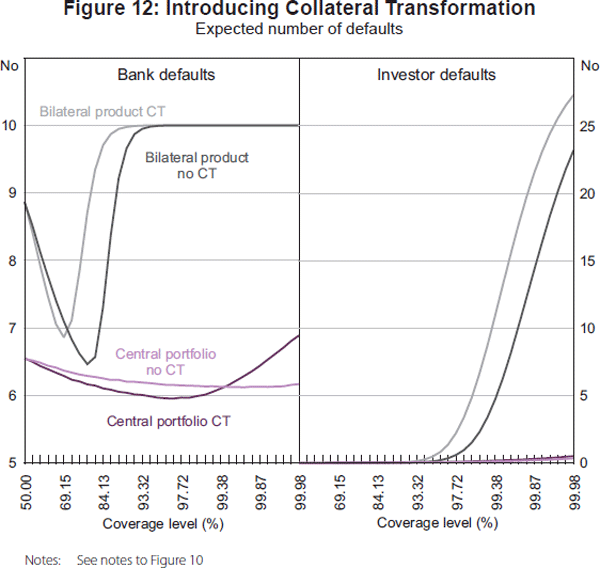
The inclusion of collateral transformation in the model materially affects the results. As might be expected, the main effect of imposing restrictions on investors' access to liquidity and establishing new interconnections is to increase the probability of default due to illiquidity for both banks and investors. For a given clearing arrangement, introducing collateral transformation lowers the optimal level of collateral coverage (Figure 12, left-hand panel) and increases the incidence of investor defaults (right-hand panel). Further, the U-shaped relationship between expected total bank defaults and collateral coverage becomes more prominent for central clearing when collateral transformation is introduced. Notwithstanding the greater netting efficiency of central clearing, at high levels of collateral coverage there is an increase in the incidence of investor defaults, in part due to the need to post a haircut with the bank that provides collateral transformation. The U-shaped curve nevertheless remains much flatter than for the clearing arrangements involving bilateral clearing, and minimum total expected bank defaults occur at a much higher level of collateral coverage.
4.4 Varying parameter values
Given the stylised nature of the model, it is useful to consider the sensitivity of the results to changes in parameters to understand the mechanisms at play. The size and composition of balance sheets are particularly important because they determine the absolute value of IA available to be converted to HQLA: a larger balance sheet relative to the size of derivative positions allows more IA to be encumbered before liquidity strains arise. Figure 13 shows that the total expected number of bank defaults declines as the balance sheet size increases, but at a decreasing rate. Since bank equity is a defined percentage of liabilities, balance sheet size also determines the size of accumulated variation margin or collateral transformation losses that may be absorbed before a bank becomes insolvent. Unsurprisingly, as the share of equity increases, the minimum number of bank defaults observed under each clearing arrangement declines for a given balance sheet size and size of OTC derivative positions.
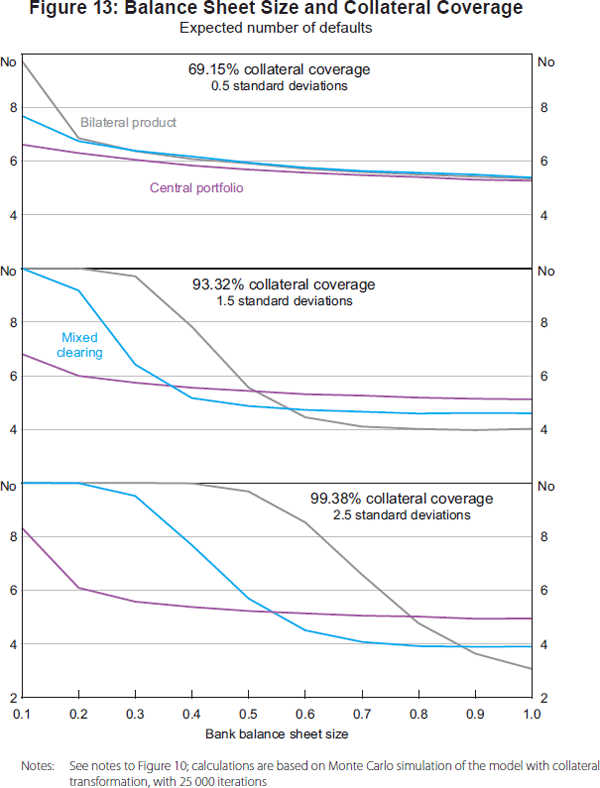
Assumptions about the volatility of prices also affect the results. As the volatility of derivative prices increases, collateral requirements increase and a bank has less capacity to absorb any variation margin or collateral transformation losses, again for a given balance sheet size. The volatility of IA prices is also an amplifier in the model. As IA price volatility increases, the minimum number of bank defaults observed for any given level of collateral coverage under each clearing arrangement also increases. At the same time, with higher volatility, larger falls in the price of IA may be observed. For both banks and investors, the incidence of such large falls ‘squeezes’ the stock of unencumbered assets on balance sheets and thereby reduces access to liquidity. As a result, even for the relatively collateral-efficient central clearing arrangements, the incidence of investor default rises with IA price volatility at higher levels of collateral coverage.
Another parameter that has been introduced in the dynamic model is the haircut on IA used as collateral to obtain HQLA. Because haircuts are used to mitigate the risk that the value of collateral will fall should it need to be liquidated, they are higher for assets with more volatile prices and that may be less likely to hold their value in stressed market conditions. Unsurprisingly, larger haircuts lead to a material reduction in the incidence of bank insolvency (for a given level of IA price volatility) in our model, particularly for centralised clearing arrangements. However, increasing haircuts will eventually increase the risk of investor default due to illiquidity. Haircuts therefore represent another channel by which dependence on the core for access both to clearing arrangements and HQLA may shift risk to the periphery.
Given that the prices of IA do not respond endogenously to changes in market conditions in the model, haircuts do not either. However, recent experience shows that increases in haircuts in response to rising price volatility were an important channel through which liquidity stresses were amplified and transmitted across financial markets. This was apparent in OTC derivative markets, and perhaps more dramatically in repo markets (Gorton and Metrick 2012). Indeed, the procyclicality of haircuts and the ability for this to amplify the effects of financial stress has been noted by policymakers as an area that deserves further consideration as a part of the regulatory reform agenda (CGFS 2009, 2010a).
Section 3.4.3 showed that if some subgroup of the periphery has directional derivative positions, the multilateral netting benefits of central clearing arrangements diminish. Figure 14 shows that this effect is also observed in the extended model. While for a given level of collateral coverage the expected incidence of bank defaults remains lower with central clearing, the steady rise in expected defaults as directionality increases is notable. Particularly striking is the finding that where margining in a centrally cleared setting is product based – or equivalently, where central clearing is fragmented across products – the incidence of bank defaults rises sharply at high levels of collateral coverage. An important driver of these results is the sharp increase in the incidence of illiquidity among investors as directionality increases. Once again, product-based margining or fragmentation in a centrally cleared setting significantly erodes the benefits of central clearing for investors, leaving the profile of investor defaults very similar to that in the mixed clearing setting.
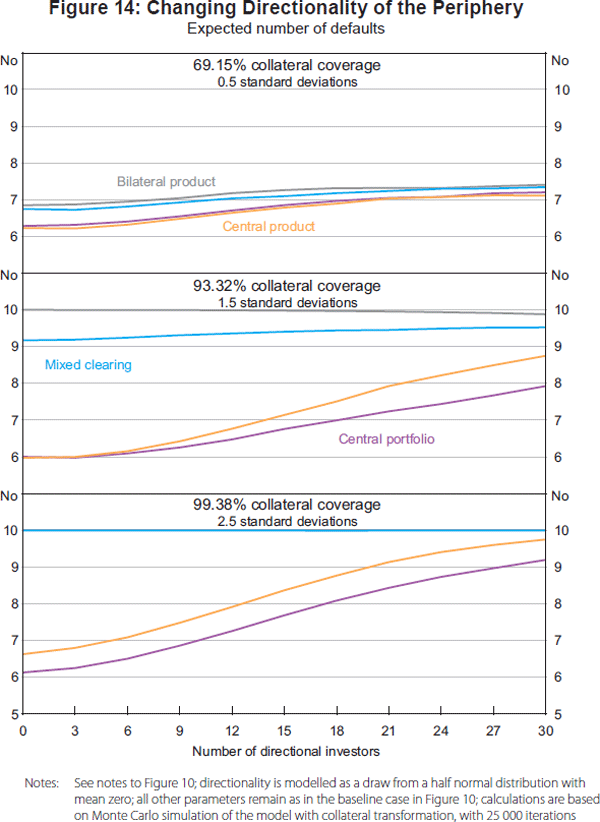
4.5 Summary
While based on a highly stylised model, the results in this section underline the benefits of central clearing, while also drawing out the implications of higher collateral demand for financial stability. The analysis reveals a trade-off between the effect of collateral in reducing the risk of insolvency and its effect on agents' liquidity. In particular, we show that there is likely to be an optimal level of collateral coverage, which will depend on the netting efficiency of clearing arrangements, the extent to which margin methodologies take account of correlations between products, and the characteristics of products and agents.
This trade-off is accentuated when we assume that agents in the periphery have limited access to liquidity and rely on core banks' provision of collateral transformation services. The new interconnections arising from such dependence become an additional channel for contagion between the core and the periphery, and the haircuts imposed on investors in relation to collateral transformation transactions become an additional source of encumbrance which amplifies the liquidity risk that investors face.
5. Policy implications
The analysis presented in Sections 3 and 4 broadly supports some of the main arguments for increasing collateralisation and moving OTC derivative transactions to central clearing. However, the analysis also draws out some factors that might limit the effectiveness of these reforms. This gives rise to a number of policy messages that we consider under three headings: network structure (Section 5.1); optimal collateral coverage (Section 5.2); and collateral shortages (Section 5.3).
5.1 Network structure
The analysis in Sections 3 and 4 suggests that a disproportionate share of the netting benefits associated with central clearing will generally accrue to core institutions, and that the financial stability benefits of the OTC derivative reforms are likely to derive primarily from core institutions participating in central clearing and collateralisation. Indeed, the analysis raises the question whether the incremental benefits of collateralising trades executed with the periphery will outweigh the additional cost of the system's increased vulnerability to liquidity problems.[15] It may be that stability objectives could be best realised if collateralisation and central clearing requirements were imposed only on core institutions and the very largest peripheral institutions.[16]
Our analysis provides a framework for examining the relevant interactions, with three messages in particular emerging:
- Product and agent characteristics. The distribution of benefits depends on a number of factors, including: the size of positions in the periphery; the size of the core relative to the periphery; the number of derivative products; and the variance and covariance of both prices and positions across products. The directionality of positions in the periphery is particularly important, since this will have implications for the scope for multilateral netting of exposure in the centrally cleared scenarios. These characteristics should therefore be taken into account by policymakers when setting the scope of requirements around collateralisation and central clearing.
- Cross-product netting. To the extent that our representation of the core-periphery network structure is reasonable, the scope for the periphery to benefit from multilateral netting will be limited, even abstracting from directionality. If exposures between the core and periphery are nevertheless deemed to be sufficient in size to be relevant to financial stability, and therefore warrant being collateralised, it is important to minimise vulnerability to liquidity risk, by ensuring that clearing arrangements avoid excessive fragmentation and maximise the scope for cross-product offsets in setting margin requirements (to the extent that it is prudent to do so). For instance, market participants may select clearing arrangements that allow for margin offsets in portfolios of closely related OTC derivative products (e.g. offsets across interest rate products denominated in different currencies), or between OTC derivative products and closely related exchange-traded products (e.g. interest rate swaps and interest rate futures).
- Collateral transformation. As we have discussed, collateral transformation may emerge as a response to the increased demand for collateral arising from OTC derivative regulation if institutions (most notably, those in the periphery) caught by these regulations are not natural holders of collateral-eligible assets on their balance sheets. Our model suggests that where peripheral institutions have limited access to liquidity and rely on collateral transformation, the optimal level of collateral coverage is likely to be lower for all clearing arrangements. This should again be recognised in setting policy in this area and, given the potential additional stability risks that may emerge, policymakers should closely monitor the scale of such activity and intermediaries' risk management practices.
5.2 Optimal collateral coverage
Perhaps the most striking result in the model is the trade-off between insolvency and illiquidity as collateral coverage increases; that is, there is a point at which sourcing collateral-eligible securities and encumbering assets to meet collateral requirements creates liquidity strains that eventually offset the benefits from collateralisation in terms of reduced risk of insolvency. The model illustrates this trade-off with a very simple balance sheet structure. Nevertheless, notwithstanding the simplification, the results from our model underscore the increasing policy interest in asset encumbrance and the message that encumbrance to meet higher collateralisation requirements can be a source of vulnerability in the financial system (Debelle 2011; Haldane 2012; CGFS 2013; Gai et al this volume).
Using bank defaults as the metric for financial stability (recognising that with highly stylised agents and balance sheets, the numbers of defaults generated in the model should not be taken too literally) the model provides some clear qualitative guidance about the optimal level of collateral coverage under alternative clearing arrangements in a dynamic setting. In particular, the model demonstrates that more netting-efficient clearing arrangements allow the market to support a higher level of collateralisation – that is, the optimal trade-off between insolvency risk and illiquidity risk is observed at a higher level of collateral coverage. It may be, therefore, that the required level of collateral coverage for OTC derivative transactions in products that do not meet the prerequisites for central clearing (e.g. products that are insufficiently standardised, or cannot otherwise be effectively risk managed by a CCP) should be lower than that for transactions in centrally cleared products, precisely to reflect the higher risk of illiquidity in less netting-efficient bilateral arrangements.[17]
The model also suggests that questions around the optimal level of collateralisation should be considered in conjunction with decisions about the optimal level of bank equity. As noted in Section 4.4, both equity and collateral reduce the risk of bank default, so more mitigation through one channel suggests that the other form of mitigation can be used less actively. Importantly, however, these two channels have quite different implications for the distribution of risks. In particular, collateral is a ‘defaulter pays’ tool, which mitigates counterparty risk but can create liquidity risks, while equity is designed to absorb losses on a bank's own balance sheet. The cost of raising equity is not explicitly captured in our model, but in a richer setting it may be that an optimal mix of equity and collateral coverage would be observed.
5.3 Collateral shortages
The paper has assumed that there is no aggregate shortage of HQLA, and that an unlimited amount was available from an exogenous (un-modelled) Securities Market. This is likely to be a reasonable assumption in aggregate and in normal times. However, there are some jurisdictions, such as Australia, with shortages of domestic-currency HQLA, and, as the financial crisis demonstrated, when financial institutions have concerns about their access to liquidity and hoard HQLA on their balance sheets, it can be difficult to obtain HQLA at any price. Our model suggests that the increase in collateral demand associated with OTC derivative reform could lead to more frequent cases of short-term liquidity problems due to increased encumbrance.
In normal times, a shortage of HQLA will result in an endogenous price response, which could encourage an increase in supply. It has been argued that this mechanism was an important driver of the growth in HQLA supplied by the private sector in the mid 2000s, primarily through securitisation (Bernanke et al 2011; Pozsar 2011). The other obvious source of HQLA is government debt, which is more likely to hold its value in stressed financial market conditions because governments have the ability to raise revenue through taxation. However, as illustrated by recent events, debt sustainability considerations can place a limit on the ability of a sovereign to successfully create new HQLA through debt issuance (IMF 2012).
Another channel through which collateral shortages can be alleviated is through central bank policy. Central banks are the ultimate source of liquidity, and so the assumption that there is no liquidity shortage in the model implicitly requires that the central bank is monitoring conditions in funding markets for signs of stress, such as sharp increases in prices for HQLA, and is willing to respond. Central banks have a number of different tools available to them in this regard. In the case of short-term idiosyncratic liquidity shortages, the most appropriate tool is collateralised lending at a penalty rate through the discount window.
A more generalised liquidity shortage that manifests as an increase in demand for HQLA and falling prices for less-liquid assets requires a different solution. Central banks can increase system liquidity through collateralised lending in their standard market operations. However, Singh and Stella (2012) observe that this may be ineffective at alleviating generalised liquidity stresses if central banks attempt to increase liquidity by lending against collateral for which there is excess demand. In this case, central banks can only increase liquidity by lending against assets that are relatively illiquid and are experiencing excess supply. This will typically involve broadening the set of assets that are eligible as collateral in central bank operations, which may be done to increase liquidity in specific, potentially systemically important, asset markets. In conditions of more severe market dysfunction, it may be necessary for central banks to purchase illiquid assets outright to minimise fire sales and support prices for distressed assets. These actions were taken in a number of jurisdictions during the course of the financial crisis.
Central banks may also take actions to alleviate liquidity stresses that arise because the distribution of the supply of HQLA and the distribution of demand do not match up. In the model presented in Section 4, this is characterised by the banks in the core having direct access to HQLA, while institutions in the periphery do not. This may arise, for instance, because institutions in the periphery do not have direct access to the central bank. In a domestic context, a central bank can affect the distribution of HQLA by broadening the set of counterparties to which it is willing to lend on a collateralised basis, or making lending to core banks conditional on providing liquidity to some subsets of the periphery.
The distribution of HQLA can also become problematic if the excess demand is for HQLA that is not denominated in domestic currency. In this case, the local central bank is not the ultimate source of liquidity. This situation did occur during the financial crisis (CGFS 2010b), and could arise in the OTC derivative market, given its global nature. In particular, there could be extensive use of non-domestic CCPs, particularly by institutions in the periphery, in order to maximise netting benefits and minimise fragmentation (as discussed in Section 5.1). In this circumstance, the policy options include swap facilities between central banks. This proved to be an effective way for central banks to provide liquidity in a non-domestic currency, and for the originating central banks to minimise their exposure to institutions about which they potentially had very little information.
6. Conclusions
With national jurisdictions currently well advanced in the implementation of G20 commitments around collateralisation and central clearing of OTC derivatives, this paper has considered the important question of how differences in the characteristics of agents and products might in some circumstances have implications for the effectiveness of the reforms. The paper has done so by modelling the system as a core-periphery network of banks and investors, and has examined how network structure might affect netting efficiency and collateral demand under alternative clearing arrangements. It has also considered new sources of interdependence between the core and periphery; in particular, by assuming that restricted access to liquidity for the periphery requires that investors source HQLA from the core via collateral transformation.
The paper has drawn out a number of key messages, relevant to the ongoing policy debate on implementation of the reforms. Most notably, the paper has illustrated how network structure and the size and nature of peripheral exposures – e.g. small, directional positions with the core – may limit netting opportunities for the periphery and may increase their vulnerability to liquidity risk in collateralised bilaterally or centrally cleared settings. In this sense, when considering the implications of higher collateral demand, it is important to look beyond the aggregate availability of HQLA to also consider the distribution. Given the stylised nature of the model, further work is needed to strengthen the conclusions, including: enriching the representation of agents' balance sheets; endogenising the price of illiquid assets; and calibrating model parameters to real world observations, so as to better establish the economic relevance of the results.
Footnotes
The views expressed are the authors and do not necessarily reflect those of the Reserve Bank of Australia. [*]
Interoperability between CCPs could, in principle, reduce the costs of un-netting arising from fragmentation in clearing venues (Cox et al 2013). However, interoperability is currently observed primarily between CCPs operating in cash equity markets, rather than derivative markets where contracts are longer dated, principal values are higher, and price volatility is often greater. Notwithstanding their support for interoperability in cash equity markets, European regulators and legislators have reserved their position on derivative interoperability, with the European Commission undertaking to assess the case for interoperability in derivative markets by December 2014. It may, therefore, be a considerable time before interoperability can be entertained in OTC derivative markets. [1]
The degree of financial exposure between a clearing agent and its clients ultimately depends on whether client positions and collateral are commingled with those of the clearing agent, segregated in an omnibus client account with fellow clients, or individually segregated. It also depends on whether the clearing agent extends credit or provides ancillary services such as collateral transformation. [2]
Consider the case of an asset price shock. The collateral transformation provider may respond in several ways: a mark-to-market call for additional collateral; an increase in haircuts; a narrowing of the range of less-liquid assets it is willing to accept as security for its loan of HQLA; or a cessation of its collateral transformation service. Each response could trigger some funding stress for the customer, with potentially procyclical implications for the broader network. If the collateral transformation provider responded by altering its own collateral-acceptability criteria or withdrawing its service entirely, the customer would be forced either to liquidate its derivative positions, or alternatively liquidate some of its less-liquid assets, most likely at fire-sale prices, in order to raise the HQLA it needed to continue to support these positions. [3]
The potential for stress to feed back to CCPs in such circumstances has also been recognised. As observed by IMF (2012, p 120), ‘large banks that are also clearing members may offer collateral transformation services to their customers to turn less liquid assets into CCP-acceptable ones through repos and swaps. This could potentially exacerbate liquidity pressures for CCPs during market downturns, when clearing members would need to provide liquid funds for their clients at a time when they themselves are being subjected to a liquidity freeze’. [4]
For a more detailed discussion of the concept of collateral velocity and its potential importance in understanding the evolution of the shadow banking sector, see Singh (2011). [5]
The margin rate, md, will be equal to the standard deviation of price movements on product d, σd, multiplied by 2.33, the cut-off for the 99th percentile in the standard normal distribution. [6]
In this case, mfij = 2.33×σfij, where
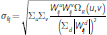 .
[7]
.
[7]
In this case, mfij = 2.33×σfi, where
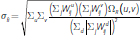 .
[8]
.
[8]
It can be shown that outcomes for exposure and collateral relative to total notional outstanding are equivalent whether the number of banks (investors) is varied keeping the total system notional position fixed, or keeping the position size per agent fixed. [9]
The assumption that prices follow a random walk and have constant variance is in contrast to many models that explore the role of collateral in the dynamics of a financial crisis (for example, Kiyotaki and Moore (1997), Brunnermeier and Pedersen (2009) and Anand, Chapman and Gai (2012)). In these models, when liquidity becomes scarce, the price of relatively illiquid assets falls relative to HQLA, which leads to margin calls for transactions where these assets have been used as collateral. This in turn can lead to fire sales and further falls in relative prices and market liquidity, and further contagion. Allowing this transmission mechanism to operate is likely to amplify the dynamics in our model, and this extension is left to further research. Endogenous prices are also important during a transition from one set of clearing arrangements to another. This is not relevant in the current context because we are comparing dynamics under different arrangements, not the transition between clearing arrangements. [10]
The allocation of unfunded losses in the CCP case reflects the mutualisation principle that characterises CCPs' activities. It simplifies the risk frameworks typically observed, however, in that CCPs generally also have a layer of ‘funded’ financial resources – a default or guarantee fund – comprising up-front contributions from participants and the CCP itself. In not modelling this layer, our model understates the liquidity cost of central clearing. [11]
We focus on just three arrangements to simplify the exposition. Since the chosen arrangements include those that exhibit the greatest (central clearing with portfolio margining) and least (bilateral clearing with product-based margining) netting and collateral efficient arrangements in the baseline model, they cover the broad span of outcomes. Results for the other clearing arrangements are available from the authors, on request. [12]
Note that in this model banks can only default for one reason. Therefore, if a bank defaults due to illiquidity, it cannot also default due to insolvency. An increase in the incidence of illiquidity therefore contributes to the decrease in the incidence of insolvency, steepening the downward slope of the insolvency line. [13]
This increases the receiving bank's assets, which are funded by debt liabilities and equity in equivalent proportion to the original liability mix. [14]
Although this paper takes the core-periphery structure as given, further insights into the costs and benefits of increasing the use of central clearing and collateralisation between the core and periphery may come from thinking about why this structure formed in the first place. Babus (2011) argues that a core will form endogenously for a network of OTC derivative transactions where long-term relationships are based on transaction fees and more ad hoc transactions require collateralisation. In this case, if transaction fees are lower than collateralisation rates, it pays for institutions that do not regularly transact with the same counterparty to form a long-term relationship with an intermediary (core) institution. If this model is correct, policymakers need to argue that the efficiency gains from intermediation are not sufficient to offset unmodelled costs, such as financial stability considerations, to justify some aspects of regulatory change. [15]
This statement refers solely to netting and collateralisation. As noted in Section 2, central clearing may offer other benefits, such as standardisation, operational efficiencies, and centralised default management. These may, in some circumstances, deliver system-wide benefits if extended to certain peripheral institutions, particularly those with high trading volumes. [16]
New international standards for initial margining of non-centrally cleared OTC derivatives, by contrast, envisage a level of collateral coverage equivalent to that under central clearing (see Section 2.2 and BCBS-IOSCO (2013)). An important consideration in developing these standards has been to incentivise central clearing by ensuring that there is no collateral cost advantage to bilateral clearing. For products that do not meet the prerequisites for central clearing, however, these incentives will not be relevant. [17]
References
Anand K, J Chapman and P Gai (2012), ‘Covered Bonds, Core Markets, and Financial Stability’, Humboldt University, Collaborative Research Center, SFB 649 Discussion Paper 2012-065.
Babus A (2011), ‘Endogenous Intermediation in Over-the-Counter Markets’, unpublished manuscript, Imperial College London. Available at <http://www.anababus.net/research/otc.pdf>.
BCBS (Basel Committee on Banking Supervision) (2012), Results of the Basel III Monitoring Exercise as of 31 December 2011, Bank for International Settlements, Basel.
BCBS-IOSCO (Board of the International Organization of Securities Commissions) (2013), Margin Requirements for Non-Centrally Cleared Derivatives: Second Consultative Document, Bank for International Settlements, Basel.
Bech ML and E Atalay (2010), ‘The Topology of the Federal Funds Market’, Physica A: Statistical Mechanics and its Applications, 389(22), pp 5223–5246.
Bernanke BS, C Bertaut, L Pounder DeMarco and S Kamin (2011), ‘International Capital Flows and the Returns to Safe Assets in the United States, 2003–2007’, Board of Governors of the Federal Reserve System, International Finance Discussion Paper No 1014.
Brunnermeier MK and LH Pedersen (2009), ‘Market Liquidity and Funding Liquidity’, The Review of Financial Studies, 22(6), pp 2201–2238.
Cecchetti SG, J Gyntelberg and M Hollanders (2009), ‘Central Counterparties for Over-The-Counter Derivatives’, BIS Quarterly Review, September, pp 45–58.
CGFS (Committee on the Global Financial System) (2009), The Role of Valuation and Leverage in Procyclicality, CGFS Papers No 34, Bank for International Settlements, Basel.
CGFS (2010a), The Functioning and Resilience of Cross-Border Funding Markets, CGFS Papers No 37, Bank for International Settlements, Basel.
CGFS (2010b), The Role of Margin Requirements and Haircuts in Procyclicality, CGFS Papers No 36, Bank for International Settlements, Basel.
CGFS (2013), Asset Encumbrance, Financial Reform and the Demand for Collateral Assets, CGFS Papers No 49, Bank for International Settlements, Basel.
Cox N, N Garvin and G Kelly (2013), ‘Central Counterparty Links and Clearing System Exposures’, RBA Research Discussion Paper No 2013-12.
CPSS-IOSCO (Committee on Payment and Settlement Systems and Technical Committee of the International Organization of Securities Commissions) (2012), Principles for Financial Market Infrastructures, Bank for International Settlements, Basel.
Craig B and G von Peter (2010), ‘Interbank Tiering and Money Center Banks’, BIS Working Papers No 322.
Debelle G (2011), ‘The Present and Possible Future of Secured Issuance’, Address to the Australian Securitisation Forum Annual Conference, Sydney, 21 November.
Duffie D, A Li and T Lubke (2010), ‘Policy Perspectives on OTC Derivatives Market Infrastructure’, Federal Reserve Bank of New York Staff Report No 424.
Duffie D and H Zhu (2011), ‘Does a Central Clearing Counterparty Reduce Counterparty Risk?’, The Review of Asset Pricing Studies 1(1), pp 74–95.
Ellis R (2012), ‘Collateral Transformation: Liquidity and Market Risk Issues’, White paper, Sapient Global Markets.
ESRB (European Systemic Risk Board) (2012), ‘Macro-Prudential Stance on Eligible Collateral for Central Counterparties in Response to a Consultation by ESMA – Based on Article 46 of the EMIR Regulation’, Accompanying document to ESRB/2012/3.
FSB (Financial Stability Board) (2010), ‘Implementing OTC Derivatives Market Reforms’, 25 October.
Gai P, A Haldane and S Kapadia (2011), ‘Complexity, Concentration and Contagion’, Journal of Monetary Economics, 58(5), pp 453–470.
Gorton G and A Metrick (2012), ‘Securitized Banking and the Run on Repo’, Journal of Financial Economics, 104(3), pp 425–451.
G20 (Group of Twenty) (2009), ‘Leaders' Statement: The Pittsburgh Summit’, 24–25 September.
Haldane A (2012), ‘Financial Arms Races’, Speech at the Institute for New Economic Thinking, The Centre for International Governance Innovation, and the Mercator Research Institute on Global Commons and Climate Change Third Annual Plenary Conference ‘Paradigm Lost: Rethinking Economics and Politics’, Berlin, 12–15 April.
Heath A and MJ Manning (2012), ‘Financial Regulation and Australian Dollar Liquid Assets’, RBA Bulletin, September, pp 43–52.
Heller D and N Vause (2011), ‘Expansion of Central Clearing’, BIS Quarterly Review, June, pp 67–81.
IMF (International Monetary Fund) (2012), Global Financial Stability Report: The Quest for Lasting Stability, World Economic and Financial Surveys, IMF, Washington DC.
ISDA (International Swaps and Derivatives Association) (2012), ‘Initial Margin for Non-Centrally Cleared Swaps: Understanding the Systemic Implications’, November.
Jackson JP and MJ Manning (2007), ‘Comparing the Pre-Settlement Risk Implications of Alternative Clearing Arrangements’, Bank of England Working Paper No 321.
Kiyotaki N and J Moore (1997), ‘Credit Cycles’, Journal of Political Economy, 105(2), pp 211–248.
Manning MJ, A Heath and J Whitelaw (2010), ‘The Foreign Exchange Market and Central Counterparties’, RBA Bulletin, March, pp 49–57.
Markose SM (2012), ‘Systemic Risk from Global Financial Derivatives: A Network Analysis of Contagion and Its Mitigation with Super-Spreader Tax’, IMF Working Paper WP/12/282.
Pirrong C (2012), ‘Clearing and Collateral Mandates: A New Liquidity Trap?’, Journal of Applied Corporate Finance, 24(1), pp 67–73.
Pozsar Z (2011), ‘Institutional Cash Pools and the Triffin Dilemma of the U.S. Banking System’, IMF Working Paper No WP/11/190.
Sidanius C and F Zikes (2012), ‘OTC Derivatives Reform and Collateral Demand Impact’, Bank of England Financial Stability Paper No 18.
Singh M (2011), ‘Velocity of Pledged Collateral: Analysis and Implications’, IMF Working Paper No WP/11/256.
Singh M (2013), ‘The Changing Collateral Space’, IMF Working Paper No WP/13/25.
Singh M and P Stella (2012), ‘Money and Collateral’, IMF Working Paper No WP/12/95.
Tabb A (2012), ‘Optimizing Collateral: In Search of a Margin Oasis’, TABB Group Vision Note, June.
Upper C and A Worms (2004), ‘Estimating Bilateral Exposures in the German Interbank Market: Is There a Danger of Contagion?’, European Economic Review, 48(4), pp 827–849.