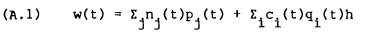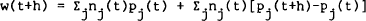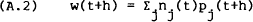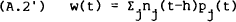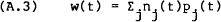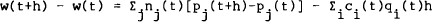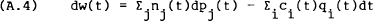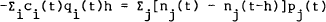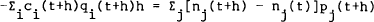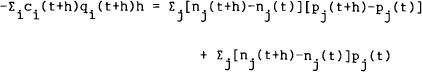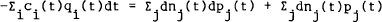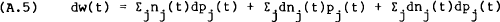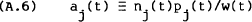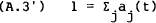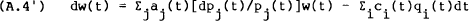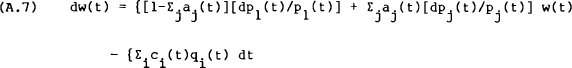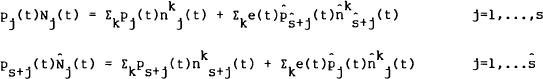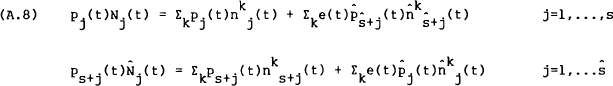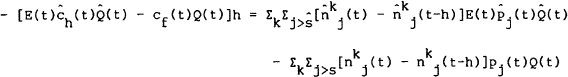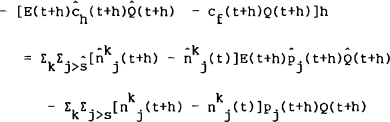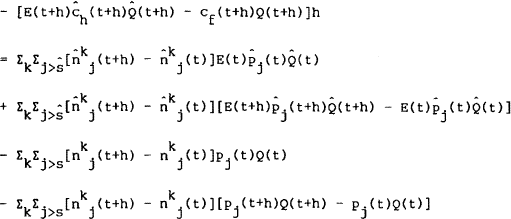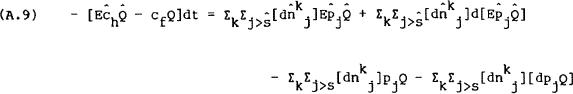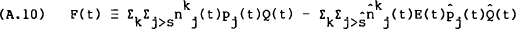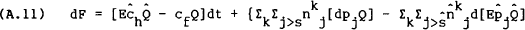RDP 8610: Equilibrium Exchange Rates and a Popular Model of International Asset Demands: An Inconsistency Appendix: Derivation of Continuous Time Constraints

DERIVATION OF CONTINUOUS TIME CONSTRAINTS

The assumption of Ito processes for the dynamics of asset prices and exchange rates means that functions involving these variables will be right-continuous functions of time. They will be differentiable in the stochastic, but not in the normal, sense. Thus, budget constraints and equilibrium conditions need to be specified consistently with the properties of stochastic calculus. This Appendix presents consistent derivations of these constraints from an underlying discrete time model.

A.l Budget Constraints

Assume there are planning periods of h time units in length and that agents make expenditure/investment plans at time t for the period [t,t+h) such that equilibrium occurs at the beginning of the period, i.e., at t. So, given their stock of real wealth, w(t), and current (deflated) prices, q_i(t) and p_j(t), agents choose their instantaneous rates of flow of consumption goods for the period and their asset stocks to be held during the period,

At the end of this planning period, the agent's stock of wealth will be increased (decreased) by the amount of capital gains (losses),

that is,

This means that wealth at the end of period [t−h,t), i.e., just before the beginning of period [t,t+h), is

The budget constraint for period [t,t+h) is given by equating equations (A.1) and (A.2′). However, from Foley (1975), Hay (1970) and Meyer (1975) one would expect that this single budget constraint in discrete time would give rise to two constraints in continuous time as the planning interval is allowed to shrink to zero. The first of these, the stock (or balance sheet) constraint, may be derived from (A.2) by using the right-continuity property of Ito processes and taking limits as h → 0,

The second is the flow (or financing) constraint. Taking equation (A.1) from equation (A.2) gives,

Again take limits as h → 0 to give,

In order to illustrate the similarity of the structure of this constraint with the balance of payments equilibrium condition to be derived below, consider Merton's (1971) derivation. Equating equation (A.1) and equation (A.2′) in the discrete time model gives,

which needs to be incremented to take advantage of the right-continuity property,

From Ito's Lemma, it is known that the difference expression on the right of this equation contains terms of order √h, and therefore the equation must be expanded before taking limits,

Taking limits as h → 0 yields,

which may be compared with equation (A.4) to deduce,

This is precisely the same as the result of applying Ito's Lemma to the stock constraint, equation (A.3). The last terra does not vanish on substitution as it does in the normal calculus because it involves the product of terms of order √h rather than of order h.

For much of the analysis it is convenient to work in terms of asset shares,

Substituting into equation (A.3), the stock constraint becomes,

Using this in equation (A.4) gives the flow constraint,

These two constraints may now be combined,

where the summation over j now runs from 2 to S. There is no longer an explicit constraint on the a_j's because they are now only defined for j=2,…S. Hence (A.7) may be used as the sole budget constraint.

A.2 Equilibrium in Asset Markets

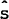Without loss of generality, assume that there are just two countries. (A “hat” will be used to denote a foreign agent.) From the point of view of a home agent, the first s of the S assets available are supplied by the home country. As seen by a foreign agent, however, these are the last s of the S assets he demands. His first assets are supplied by the foreign country, as are the last assets demanded by a home agent.

Equilibrium occurs at the beginning of the period, so equate asset supply and demand to give,

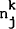
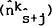where is the (exogenous) stock of the j^th home (foreign) asset, is the k^th home (foreign) agent's demand for the j^th home country asset, 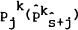is the (deflated) price of the j^th home asset in the home (foreign) currency and e is the real (deflated) exchange rate. Taking limits as h → 0,

which are the market clearing conditions for the asset markets. This gives S conditions, of which only (s−1) are independent given the aggregation of the individual (stock) budget constraints (Walras' Law).

A.3 Balance of Payments Equilibrium

For derivation purposes, consider the balance of payments of the home country, expressed in its own currency, when the first m goods are produced by it.

At the end of period [t−h,t) the net holdings of foreign assets by the home country are 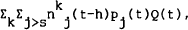whereas at the beginning of period [t,t+h) net holdings are 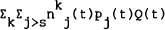. The corresponding holdings of home country assets by the foreign country are 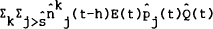and 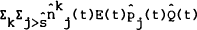respectively. 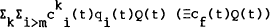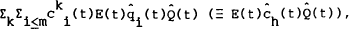The rate of nominal consumption of foreign goods chosen by the home country will be and the rate of consumption of home goods chosen by the foreign country is where the subscript i is ordered as in the home country.

Given these relationships, the balance of payments equilibrium condition for the home country is,

where the trade balance appears on the left and asset transactions on the right. As in Merton's derivation of the budget constraints shown above, this equation needs to be incremented to take advantage of the right-continuity property of Ito processes,

Again, the difference expressions on the right hand side of the equation contain terms of order √h and need to be expanded,

Taking limits gives,

which is the stochastic differential equation representing balance of payments equilibrium for the home country.

To interpret this equation, define the net foreign asset position of the home country, F(t), as

Applying Ito's Lemma to this and using equation (A.9) gives,

where the capital account is on the left and the current account on the right; the trade account is the first term on the right and the service account is the term in curly brackets.