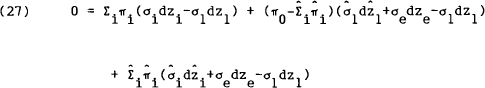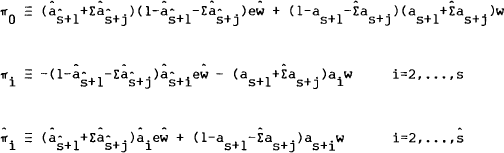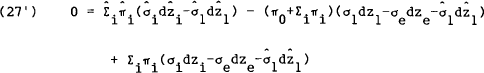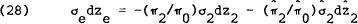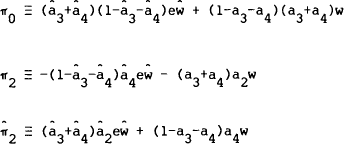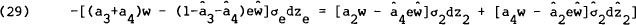RDP 8610: Equilibrium Exchange Rates and a Popular Model of International Asset Demands: An Inconsistency 6. The General Case

The last example assumed the existence of a real riskiness asset in each country. When there are no such assets, the analysis must be expanded to include consideration of terms in σ₁dz₁ and 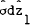. It may then be shown that the coefficient on the σ₁dz₁ term in the balance of payments constraint is simply the sum of those on −σ_idz_i for i=2,…,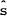 (equation (26a)) less the one on σ_edz_e (equation (26b)). Similarly, the coefficient on the 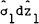term is that on σ_edz_e less the sum of those on for i=2,…,s (equation (26c). Hence the additional restrictions, that the coefficients on σ₁dz₁ and 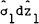are also zero, are not independent of those in equation (26). The above analysis then implies that the only solution to the stochastic part of the balance of payments constraints is that one of the σdz's is a linear combination of the others such that,

where,

Equation (27) shows that a linear combination of the returns on the zero wealth portfolios constructed by taking a long position in one of the j=2,…,S assets and a short position in the home country's first asset, is once again riskless. Contrary to the assumption of distinct assets, riskless portfolios of risky assets can be created. This implies that the investment opportunity set, as it is perceived by the home agent, is spanned by (S−1) of the S assets and that his covariance matrix of excess returns, Ω in equation (7), is singular. A simple rearrangement of terms in equation (27) shows that,

which implies that the investment opportunity set perceived by the foreign agent has an identical problem. Hence, the S assets are not distinct and the original maximisation problem is misspecified. From this property of the most general case, the following propositions may be proved.

Proposition 1: Under the assumption of market clearing prices, the investment opportunity set perceived by any agent is spanned by any S−1 of the S available assets.

Proposition 2: The market clearing exchange rate process cannot have an idiosyncratic risk (dz) component. Rather, exchange rate risk is a linear combination of asset market risks.

These propositions rest on the result in equation (27) which gives σ_edz_e as a linear combination of the stochastic parts of the asset prices. In order for the exchange rate to be a geometric Brownian motion process at all, the weights in this linear combination (the π's) must be constant. To see that even this possibility is inconsistent with the model, consider the case where each country supplies a real riskless asset (σ₁dz₁ and 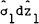are zero) and a single risky asset (s and 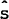are both two). Then,

where,

a₂ is the share of wealth invested in one's own country's risky asset, and a₃ and a₄ are the shares invested in the other country's riskless and risky assets respectively. Since all the a_j's are constant, the weights will be constant if and only if the ratio of home country to foreign country wealth 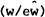is constant over time. Ito's Lemma and the budget constraints in equation (22) may be used to show that this requires,

which cannot hold simultaneously with equation (28). Hence the weights in equation (28) cannot be constants. This suggests a third proposition, which may be proved for the more general case.

Proposition 3: The market clearing exchange rate process cannot be geometric Brownian motion.