RDP 8610: Equilibrium Exchange Rates and a Popular Model of International Asset Demands: An Inconsistency 7. Concluding Observations

This paper has established that the model conventionally used in the literature on international portfolio analysis is internally inconsistent. Contrary to the assumptions of this model, the stochastic part of the market clearing exchange rate is a linear combination (with non-constant weights) of the risk components of the asset price processes. It cannot have an idiosyncratic risk component, nor can it be a geometric Brownian motion process.

The reason for this is clear. Examination of the budget constraint reveals that consumption is an instantaneous flow and asset holdings are instantaneous stocks. Instantaneous uncertainty only enters an agent's decisions via stock variables – i.e., via the real capital gains/losses he will accrue over time due to his asset holdings. Hence an agent's flow demand for foreign exchange has a risk component that is a function of asset market risk only. There is no uncertainty with respect to his demand for foreign exchange to make foreign consumption purchases. Therefore, the stochastic part of the net demand for foreign exchange by each country is simply a function only of the real risk in asset markets. The equilibrium real exchange rate stochastics can only be a function of these risks. This leads to the inconsistency result.

The inconsistency is important because one of the assumptions of the model is that agents have rational expectations. A fundamental implication of this assumption is that the price functions and dynamics “assumed” by agents in determining their portfolio demands are indeed the ones obtained from the interaction of the (assumed) supply behaviour and the aggregation of the optimal demand decisions of all agents. The model violates this necessary condition. Therefore it does not provide a micro-foundations theory of international asset demand.

This problem only arises in a model with market clearing exchange rates. Perhaps one could claim that while asset markets clear, foreign exchange markets do not? In the context of this model, however, it cannot be assumed that exchange rates are fixed, or “crawling”. In that case, the assumption of smooth continuous processes for exchange rates would be inappropriate. Even to think of exchange rate determination as a managed float, taking the parameters of its stochastic process as exogenous, is inconsistent with the spirit of the model and much of the literature in which it is imbedded. The discussion in Branson and Henderson (1985), for example, assumes that the exchange rate is endogenous and Frankel (1982) uses asset market equilibrium constraints to solve for the instantaneous means of exchange rate process, rather than the means of asset price processes.

Moreover, given the continuous time structure of the model, consumption is of an instantaneous flow dimension that is known with certainty. Only portfolio holdings are of a stock dimension that involves instantaneous real risk. The lack of clearing in goods markets (or markets other than asset markets) will not, therefore, logically impinge on the demonstration of inconsistency presented above.

The analysis involves a number of other assumptions that could be relaxed without removing the inconsistency. Each of these will be treated in turn:

1. Two agents and two countries. At the cost of severely complicating the algebra, the above argument may be reconstructed for more than one agent in each country or more than two countries. This merely adds additional terms to the constraints in the expression for the noise terms of the balance of payments. The process of differentiating and collecting terms still generates the same inconsistency result and the same three propositions.
2. Constant risk tolerance. Allowing the coefficients of risk tolerance θ(w) and 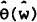to vary stochastically means that the asset shares are not constant and equation (24) does not represent balance of payments equilibrium. However, examination of the correct equilibrium condition in equation (9) shows that the same arguments apply. The additional risk introduced to agents' foreign exchange demands is the risk associated with movements in real wealth, which is only asset market risk. There is still no reason for idiosyncratic risk in the foreign exchange market, and the three propositions continue to hold.
3. Homothetic utility functions. Relaxing this assumption, of itself, only adds terms reflecting hedges against unfavourable shifts in consumption prices to agents' asset demand equations. It does not change the essence of the results. However, if the coefficient of risk tolerance is variable as well, there will be a channel for non-asset market risk to enter the foreign exchange market. This is because the θ's are then functions of both real wealth and the vector of consumption prices.^[30] To that extent, the noise term in the exchange rate process is a linear combination of those in the processes for both asset prices and consumption prices; all of the S assets are required to span the investment opportunity set, and the covariance matrix is invertible. Propositions 1 and 2 are then invalidated. Nonetheless, it is unlikely that a specification of utility functions can be found that also allows the weights to be constant. The equilibrium exchange rate is thus not geometric Brownian motion, so Proposition 3 continues to hold. Moreover, Adler and Dumas (1983) conclude that for many countries the covariance between exchange rates and consumer price indexes is low (in monthly data). This suggests that goods market risk is not a large component of exchange rate risk. Hence, the homotheticity assumption may not be an inappropriate modeling strategy.
4. Capital gains are sole source of income. The addition of wage income or transfer payments to agents' budget constraints does not change the results of the analysis unless that income is of a stock dimension (i.e., involves instantaneous uncertainty). Even with such a source of additional uncertainty, it is not clear that conditions exist under which the weights (in the solutions for the parameters of the exchange rate process) are constant. Thus Proposition 3 is likely to remain.
5. No monetary holdings in the model. Introducing model holdings via agents' instantaneous utility functions (directly as in Kouri (1977) or indirectly through a production function for consumption services as in Stulz (1984)) changes the asset demand equations but does not provide an independent source of risk in the foreign exchange market. All the propositions remain valid unless agents also have an associated uncertain (i.e., stock dimension) transfer payment from the government injected into their budget constraints.
6. No government demand for foreign exchange. A micro-foundations model that allows for (continuous, stochastic) government intervention in the foreign exchange market could be constructed, but then one would want to explicitly specify (or derive) the governments' intervention rules. It is not sufficient to assume that the intervention policy is whatever is required to produce a geometric Brownian motion process for the exchange rate.

These arguments suggest that relaxing any (combination) of these assumptions does not produce an equilibrium exchange rate process that is consistent with the assumptions of the model. A condition for rational expectations equilibrium is that the price functions assumed by agents are the same as those implied by the aggregation of their consumption and portfolio allocation decisions. Therefore, this model (which is commonly encountered in the literature) does not provide a consistent micro-foundations theory of international asset demand.

The model may be made into a consistent theory if more complicated Ito processes for asset prices and the exchange rate (where the parameters of the distributions are themselves stochastic) are allowed. Such models have been utilised in the international literature but, as yet, the constraints imposed by equilibrium in foreign exchange markets have not been explored. Given the assumption of market clearing under rational expectations, it may be fruitful to extend these models to explicitly allow agents to take into account the result that the equilibrium exchange rate process is a linear combination of the other stochastic processes.

Footnote

Actually the vector of consumption prices can be replaced by two price indices – one based on average and the other on marginal expenditure shares. See Breeden (1979) and Stulz (1981). [30]