RDP 8711: Deviations from Purchasing Power Parity: The Australian Case Appendix A Data and Detailed Results

Adrian Blundell-Wignall and Marilyn Thomas

September 1987

Data used in the empirical analysis includes:

quarterly and monthly data for Australia's real effective exchange rate from 1970 to March 1987 in index form (1980-Q2 = 100), from Morgan Guaranty World Financial Markets. It is calculated as the nominal effective exchange rate adjusted for differential inflation measured by the wholesale manufacturing price index – a series which is partially estimated;

  • end of quarter data for the bilateral exchange rate between the Australian and U.S. dollars;
  • quarterly terms of trade data from March 1970 to March 1987 calculated as the unit value of exports divided by the unit value of imports; and
  • monthly data for the Reserve Bank's rural commodity price index from July 1984 to March 1987. These last three series are from the Reserve Bank of Australia's research database.
Table 2
lag length (n) test-statistics for 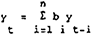Inline Equation using real US$/$A rate test-statistics for 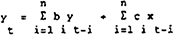Inline Equation using real US$/$A rate and the terms of trade
  Uncorrected model Corrected model
  Significant coefficients F Marginal significance less than Significant coefficients F Marginal significance less than Significant coefficients Wald Marginal significance less than
March 1070 – March 1067
2 None 0.03 0.01(A) None 0.65 0.34(A)      
4 None 0.29 O.0B(A) None 0.58 0.19(A)      
6 None 0.35 0.07(A) None 0.69 0.24(A)      
March 1970 – December 1983
2 None 0.26 0.15(A) None 1.02 0.59(A)      
4 None 0.31 0.09(A) None 0.75 0.34(A)      
6 None 0.34 0.07(A) None 0.63 0.18(A)      
March 1934 – March 1987
2 None 0.32 0.19(A) None 0.21 0.05(A) None 4.83 0.56(A)
4 None 0.73 0.3B(A) None 0.35 0.9(A) None 30.91 0.999(R)

Note
(A) denotes acceptance of the null hypothesis that all the coefficients and the intercept are jointly zero, that is, the model follows a random walk;
(R) denotes rejection of the null hypothesis, implying the model does not follow a random walk.

lag length (n) test-statistics for 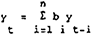Inline Equation using real US$/$A rate test-statistics for 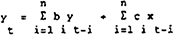Inline Equation using real US$/$A rate and the terms of trade  
  Uncorrected model Corrected model
  Significant coefficients F Marginal significance less than Significant coefficients F Marginal significance less than Significant coefficients Wald Marginal significance less than
March 1970 – March 1987
2 None 0.35 0.21(A) None 1.28 0.72(A)
4 yt−3 2.01 0.91(A) yt−3 1.66 0.88(A)
6 yt−3 1.76 0.89(A) None 1.20 0.69(A)
March 1970 – December 1983
2 None 0.07 0.03(A) None 0.6S 0.34(A)
4 None 0.23 0.05(A) None 0.SO 0.24(A)
6 None 0.18 0.01(A) None 0.34 0.02(A)
March 1984 – March 1987
2 None 0.80 0.48(A) None 1.61 0.74(A) Xt−2 39.57 0.999(R)
4 None 1.21 0.61(A) None 1.51 0.63(A) None 210.84 0.999(R)

Note
(A) denotes acceptance of the null hypothesis that all the coefficients and the intercept are jointly zero, that is. the model follows a random walk;
(B) denotes rejection of the null hypothesis, implying the model does not follow a random walk.

Table 4: January 1970 – March 1987
lag length (n) test-statistics for 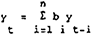Inline Equation using real US$/$A rate
  Significant coefficients F Marginal significance less than
6 yt–1 2.94 0.994(R)
12 yt–1 1.76 0.94(A)
18 yt–1 1.76 0.96(A)
Table 5: January 1970 – November 1983
lag length (n) test-statistics for 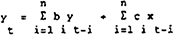Inline Equation using real US$/$A rate and the terms of trade
  Significant coefficients F Marginal significance less than
6 None 0.57 0.22(A)
12 None 0.52 0.10(A)
18 None 0.59 0.10(A)

Note
(A) denotes acceptance of the null hypothesis that all the coefficients and the intercept are jointly zero, that is, the model follows a random walk;
(R) denotes rejection of the null hypothesis, implying the model does not follow a random walk.

Table 6: December 1983 – March 1987
lag length (n) test-statistics for 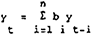Inline Equation using real US$/$A rate test-statistics for 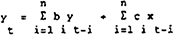Inline Equation using real US$/$A rate and the terms of trade
  Uncorrected model Corrected model
  Significant coefficients F Marginal significance less than Significant coefficients F Marginal significance less than Significant coefficients Wald Marginal significance less than
6 yt−3 1.90 0.90(A) xt−1 2.03 0.69(A) xt−1
xt−5
yt−1
yt−6		 62.51 0.999(R)
12 None 0.94 0.48(A)            
16 None 0.96 0.47(A)            

Note
(A) denotes acceptance of the null hypothesis that all the coefficients and the intercept are jointly zero, that is, the model follows a random walk;
(R) denotes rejection of the null hypothesis, implying the model does not follow a random walk.

Table 7: Results of White Test for Heteroscedasticity Ho: no heteroskedasticity
Model Lags
(months)		 Prob > Chi-Square
1970-Mar'87 1970-Dec'83 1984-Mar'87
effective(gly) without TOT 6 0.49 0.80 0.24
  12 0.37 0.60 0.26
  18 0.63 0.87 –
with TOT 6 0.74 0.98 0.10
  12 0.71 0.77 0.0001
  18 0.73 0.82  
US bilateral (gly) without TOT 6 0.32 0.22 0.18
  12 0.61 0.37 0.05
  18 0.61 0.64 –
with TOT 6 0.64 0.37 0.01
  12 0.62 0.64 0.0001
  18 0.22 0.74  
effective (mthly) without commodity prices 6 0.18 0.52 0.18
  12 0.09 0.82 0.19
  IB 0.27 0.82 0.32
with commodity prices 6 – – 0.0007

Note: Under Ho. it is assumed that the errors are independent of the regressors and that the model is correctly specified. The null hypothesis is rejected when the marginal significance level is less than that desired (e.g. 0.01, 0.05).

Table 8: Results of Breusch-Godfrey Test for First-Order Autocorrelation
HO: No First order Autocorrelation
Model Lags
(months)		 1970-Mar'87 Prob > F
1970-Dec'83		 1984-Mar'87
effective (gly) without TOT 6 0.02 0.49 0.13
  12 0.20 0.03 0.38
  18 0.02 0.09 0.20
with TOT 6 0.54 0.06 0.16
  12 0.26 0.94 0.35
  18 0.62 0.62 –
US bilateral (gly) without TOT 6 0.27 0.71 0.49
  12 0.92 0.66 0.38
  18 0.08 0.23 0.57
with TOT 6 0.73 0.48 0.27
  12 0.75 0.36 0.42
  18 1.00 0.62 –
effective (mtly) without commodity prices 6 0.01 0.42 0.02
  12 0.06 0.07 0.31
  18 0.77 0.93 0.86
with commodity prices 6 – – 0.012

Note: The null hypothesis is rejected when the marginal significance level is less than that desired (e.g. 0.01, 0.05).