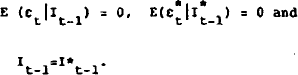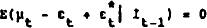RDP 8711: Deviations from Purchasing Power Parity: The Australian Case 3. The Models
September 1987
- Download the Paper 633KB
(a) A random walk model of deviations from PPP
In this section we show that it is possible to derive a random walk model of deviations from PPP from conditions of asset market equilibrium, even though the ex-ante expectation is for the constant equilibrium level to prevail. Since Adler and Lehman's finding of widespread support for the random walk hypothesis is so surprising, it is important to illustrate the kind of theoretical assumptions that would justify testing it as a null hypothesis. Alternative hypotheses which suggest that the real exchange rate reverts to an equilibrium level are too well known to require further justification in this paper.
| Let | ||
| it | = | the nominal interest rate from t to t+1, |
 |
= | expectation of the inflation rate from t to t+1, based on the information available at the end of time t−1, |
| it | = | actual inflation rate from t to t+1, measured by the wholesale manufacturing price index., |
 |
= | the expectation of the percentage change in the exchange rate from t to t + 1. based on the information available at the end of time t−1. |
| st | = | actual percentage change in the exchange rate from t to t+1, |
| It−1 | = | information available at the end of time t−1. |
An asterisk denotes a foreign country, and its absence the domestic country.
Using this, notation, we begin with the simple equilibrium condition of the asset market approach to exchange rate determination. Perfect substitutability between assets denominated in different currencies is assumed (i.e. Zero risk premium), so that the uncovered interest parity holds:
He postulate that rational expectations prevail in the spot exchange market, so that:
Subtracting 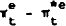 from both sides of (1) and re-arranging, we obtain:
from both sides of (1) and re-arranging, we obtain:
This simply states that the expected real interest differential between assets (bonds) denominated in different currencies equals the expected change in the real exchange rate. We further postulate that inflation expectations within bond markets are also rational, so that actual inflation rates equal expected inflation rates plus random error terms:
where
To arrive at a random walk model we also need to specify the ex-ante equilibrium condition for the roal exchange rate with which our rationally expected inflation and exchange rate changos are consistent. We assume that a zero change is anticipated. PPP is expected to prevail at the existing real exchango rate and the real interest differential is expected to be zero. Ignoring real interest rates:
By substituting (2) and (4) into (5) we obtain:
which is observable.
Following from the rational expectations assumption we have:
The ex-ante expectation that the real exchange rate will not change implies that the observed real exchange rate will follow a random walk process. There will be no systematic tendency to revert to PPP following a random deviation from parity.[3]
(b) The alternative hypotheses
The random walk model of deviations from PPP may be tested against the alternative hypothesis that there is a tendency to revert towards long-run PPP following a disturbance, as in Adler and Lehman. However, the argument that the equilibrium value of the real exchange rate is constant assumes that relative prices remain unchanged (apart from short-term cyclical fluctuations). This assumption may not be applicable to small open economies that specialise in commodity trade. Such countries may be subject to exogenous terms of trade shocks that are “permanent” – there may be trend movements, or persistent deviations from trend.
The maintenance of the equilibrium current account balance in the face of a permanent shift in the terms of trade calls for adjustments to the equilibrium real exchange rate.[4] A shift in the relative competitiveness of the bundle of goods in question is required to generate trade quantity offsets to the real gain or loss implied by the change in the terms of trade.
In this case the long-run equilibrium or “sustainable” level of the real exchange rate may not be constant, as implied by the PPP hypothesis. Shocks or innovations in the real exchange rate would revert to the terms-of-trade-modified equilibrium level. Taking account of such effects in the above model may mean that at least some of the movements in the real exchange rate may be predictable – contradicting the random walk hypothesis -given expectations about movements in commodity prices.
If the earlier model is modified to allow for terms of trade effects, equation (5) could be rewritten as:
where:
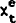 = the
expectation of the percentage change in the terms of trade from t to t+1 based on
information available at the end of time t−1.
= the
expectation of the percentage change in the terms of trade from t to t+1 based on
information available at the end of time t−1.
Making the further assumption that expectations about movements in the terms of trade (commodity prices) are rational:
Substituting (2), (4) and (7) into (8) and rearranging we obtain:
where
This contradicts the random walk model of deviations from PPP in equation 6. At least some part of real exchange rate movements will be predictable, given information about the terms of trade.
Chart 3 shows Australia's real effective exchange rate together with our terms of trade. Both rose in the early 1970s and subsequently were subject to a trend decline. One exception to this general pattern is the period from about 1960 to the end of 1983, referred to earlier in relation to the trade-weighted nominal exchange rate. The real exchange rate rises strongly, in spite of a relatively flat profile for the terms of trade.
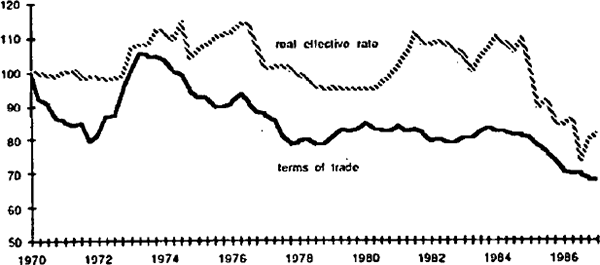
Nevertheless, there appears to be sufficient casual evidence to suggest that the terms of trade may be important in specifying an alternative to the random walk hypothesis. Consequently, we consider a more general alternative hypothesis than that adopted by Adler and Lehman: that there is a tendency for the real exchange rate to revert to an equilibrium level which may or may not be constant, depending on the importance of the terms of trade effect.
The percentage change in the real exchange rate in the random walk model (equation 6) represents the PPP innovation. Its conditional expectation given information available at the end of time t-1 is zero. This implies that in the regression model:[5]
the estimates of the bi and ci coefficients should be jointly insignificantly different from zero. Υt is the percentage change in the real exchange rate from t to t+1 and ut is a random error at period t.
The null hypothesis that the random walk model of deviations from PPP is the true model, is tested against the alternative hypothesis that information about past changes in the real exchange rate and commodity prices are relevant for predicting innovations in PPP.
Adler and Lehman test the random walk model against the less general alternative hypothesis that the real exchange rate reverts to long-run PPP. This hypothesis predicts that real exchange rate changes should be positively serially correlated, because deviations from PPP are cumulative in the short-run and, in the long run, the real exchange rate tends to revert to a constant equilibrium.
In testing the random walk model against this alternative hypothesis they implicitly restrict the ci coefficients to be zero, and test only whether the bi coefficients are jointly insignificantly different from zero. If the set of bi coefficients are jointly zero, then innovations to the real exchange rate in Adler and Lehman's regression model are serially uncorrelated. This would constitute evidence against the (less general) alternative hypothesis in favour of the random walk model.
A potential problem with this approach is that by restricting the ci equal to zero, there may be a high probability of making a Type II error – failing to reject the null hypothesis when in fact it is false. Deviations from PPP may appear to be random, when in fact they arise partly because of changes in commodity prices, which are ignored in Adler and Lehman's regression model.
The modification considered in this paper is that in the long run the real exchange rate may revert to a level that is not constant, but changes with movements in the terms of trade or commodity prices.[6] The random walk model implies that successive increments to the real exchange rate are serially independent. If the random walk model is the true model, there should be no relationship between the real exchange rate and past movements of both itself and commodity prices. If there is no serial correlation then the null hypothesis that both the bi and ci coefficients, i=l, ... , n, in equation 10 are jointly insignificantly different from zero should not be rejected by the data.
In the next section, we show that if we follow Adler sod Lehman by restricting the ci coefficients to zero, we too are unable to reject the random walk model of deviations from PPP on Australian data. However, we also show that if tested against the more general alternative the random walk model is rejected for some periods.
Footnotes
Adler and Lehmann derive this model following different assumptions to those adopted here. In particular, they assume the real interest differential is constant. A non-zero real interest differential implies expectations of perpetual' depreciation of the real exchange rate. This seems implausible without specific assumptions about trend movements in relative commodity prices. [3]
See Spencer (1983) for a derivation of the extent of adjustment of PPP consequent upon a shift in the terms of trade. [4]
We assume for simplicity that there is a linear relationship between the expected change in the real exchange rate and the expected change in the terms of trade. [5]
The PPP alternative hypothesis is a special case of this more general regression model. The ci coefficients would be jointly insignificantly different from zoro, whilo this would not be the case for the bi coefficients. [6]