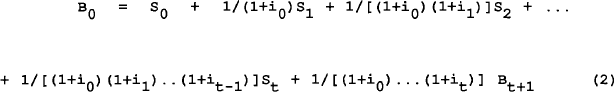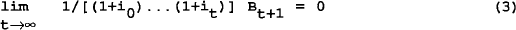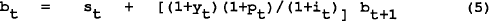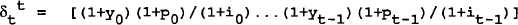RDP 8809: The Intertemporal Government Budget Constraint and Tests for Bubbles 2. The Intertemporal Government Budget Constraint

In order to examine the relationship which exists between the government's fiscal stance and the performance of the macroeconomy, the appropriate framework is the government's intertemporal budget constraint. This can be written either in nominal terms and\or as a proportion of GDP and it establishes the link which exists between the prevailing level of government indebtedness and the future debt servicing requirements.

Table 1 shows the nominal and deflated budget deficits together with the level of outstanding debt in Australia over the period 1953/54 to 1986/87. Figure 1 shows that although nominal debt outstanding has increased dramatically, the deflated series has tended towards historically low levels in recent years.

Consider first the nominal version of the government's intertemporal budget constraint which is written as equation (1).

where B denotes the level of debt prevailing at the start of the period (denoted in subscripts), S denotes the ‘primary’ surplus (i.e. the deficit net of interest payments on outstanding debt) plus seignorage and i_t denotes the nominal rate of interest which prevails between periods t and t+1. It is assumed that all debt issued matures at the end of the year. Equation (1) can be rewritten as

If we start at time t=0 and solve equation (1)′ recursively forward in time, we obtain equation (2)

which yields the intertemporal budget constraint by utilising the transversality condition that the level of outstanding nominal debt does not permanently grow at a faster rate than the nominal interest rate, i.e.,

By imposing this transversality condition (3) in equation (2) and denoting the nominal discount factor by R_t = 1/(1+i₀) … (1+i_t), we can simplify the nominal version of the government's intertemporal budget constraint to equation (2)′

which states simply that the present value of debt servicing obligations must be equal to the prevailing level of outstanding debt.

It is pertinent to note that the public sector borrowing requirement constitutes an inappropriate indicator of the government's fiscal stance. The inclusion of public trading enterprises in the measure of the deficit is misleading as these corporations resemble and act as private enterprises. From the perspective of the budget constraint, only the subsidies paid to and receipts received from these enterprises are relevant. Accordingly, the Australian government's fiscal deficit measure which is employed in this paper is obtained by aggregating the Commonwealth and State and Local authorities' revenues and outlays net of public trading enterprises.

As Blanchard, Dornbusch and Buiter (1986) point out it is illuminating to express the government's intertemporal budget constraint as a proportion of GDP. By noting that the growth rate of nominal output (Y_t+1−Y_t)/Y_t is equal to the sum of real output growth (y_t) plus inflation (p_t),

and we use this to deflate the nominal budget constraint of equation (1)′ to get

where b_t = B_t/Y_t and s_t = S_t/Y_t.

Proceeding as before, the real version of equation (2)′ is equal to

where;

This expression can be simplified to (6)′ by writing δ = (1+y)(1+p)/(1+i) where y,p and i denote respectively the long term average growth of real output, the long term average inflation rate and the long term interest rate (the analysis henceforth uses these long term averages with the bar dropped from equations);

The interesting aspect of this version of the government's intertemporal budget constraint is that it demonstrates how higher growth of nominal output (i.e. either higher real output growth and/or higher inflation) reduces the burden of debt repayments. As long as the long term average growth in nominal output exceeds the long term average nominal interest rate, the government is not constrained by the amount of debt it can service. Because this is not generally the case, however, governments are faced with a constraint which will be binding if the growth of debt equals (1+i)/(1+y)(1+p) which implies that on average new issues of bonds are restricted in their amount to cover interest payments on the current level of outstanding debt.

It is generally the case in real economic circumstances that the rate of growth of government bonds diverges from the upper limit implied by the intertemporal budget constraint. There is not necessarily a mechanism to prevent governments from issuing debt in such quantities that its future growth exceeds the sustainable rate which is implied by nominal output growth and nominal interest rates, at least over a short period of time. If this occurs, the government is said to be engaging in bubble financing of it's fiscal deficit. There is an adjustment mechanism, however, which causes the constraint to apply over time. When government debt is imperfectly substitutable for other private sector financial assets, the price of bonds must fall in order to induce portfolio balancers to take up the debt. The resulting higher debt servicing costs are also reflective of the increased incentive which is required to offset investors' uncertainty about whether the government will be able to honour it's future debt obligations.