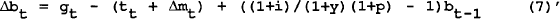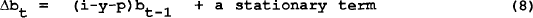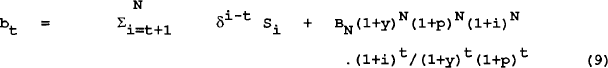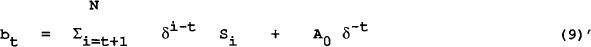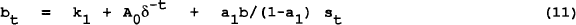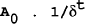RDP 8809: The Intertemporal Government Budget Constraint and Tests for Bubbles 3. Testing for Bubble Financing

In this section, we examine two tests for the existence of bubble financing in Australia over the period 1953/54 to 1986/87. The first test employs the cointegration method pioneered by Granger (1981) and Engle and Granger (1987) which has been utilised by MacDonald and Speight (1987) to examine the British case and Hakkio and Rush (1987) and Trehan and Walsh (1988) for the US. The second test investigates the price level bubble approach pioneered by Flood and Garber (1980) and adapted to examine the intertemporal government budget constraint for the US by Hamilton and Flavin (1986).

Cointegration can be defined as follows. If the components of a vector x_t have a stationary invertible ARMA representation after differencing d times, then x_t is said to be integrated of order d, i.e. x_t ~ I(d). Variables integrated of the same order are said to be cointegrated of order d,b, if there exists a linear combination of these variables such that z_t = α′x_nt is integrated of order d−b where d, b>0. In the special case where d=b, zt is stationary. This implies that the general trend in each series is the same; there is a common path followed by the two series which, although it may not hold at all points, is returned to time and time again.

The first of these tests is derived from equation (1). This can be rearranged to give the following equation:

where the lower case letters g,t,m, and b refer respectively to the government spending, taxation, the money base and debt outstanding deflated by GDP. Seignorage (financing the deficit by expansion of the money base)^[1] is included as the government can simply issue money to pay its bills.

When the constraint is binding, the change in the level of bonds must be stationary. This is proved formally for the nominal case in Trehan and Walsh (1988)^[2]. The point is seen by rearranging equation (7) in the form

which is approximately (and exactly in continuous time) equal to

The last term here is simply the interest payments on debt deflated by GDP growth and inflation. For debt not to be explosive the right hand side of the above equation must be stationary (it may have a negative deterministic component over a sample if debt is being repaid). This differs from the related equation in Trehan and Walsh (1988) as it allows for the possibility that inflation and/or economic growth may finance the deficit. Trehan and Walsh (1988) point out that the requirement that the deficit excluding interest payments be stationary for sustainability (as tested in Hakkio and Rush (1987) and MacDonald and Speight (1987)) is not sufficient; the deficit including interest rates must be stationary.

There is a special case when these two hypotheses will be identical. If the deficit excluding interest rates is stationary (as in the null hypothesis of Hakkio and Rush (1987)) equation (7)′ ′ reduces to

The change in the bond series will be stationary if y+p is greater than i. This corresponds to a root of the bond series of 1+i−y−p which is less than one. The bond series and thus the deficit including as well as excluding the deficit is stationary. This shows that the tests for a deficit including and excluding interest payments are equivalent in this case.

In general, however, the right hand side of equation (7)′ ′ will be stationary if the sum of the trends in each of the variables cancel. This allows for the possibility that the deficit excluding interest payments to be non stationary and still satisfy the constraint if it is cointegrated with interest payments.

One test of the above hypothesis is to test the right hand side of equation (7)′ for stationarity. This is equivalent to imposing a cointegrating relationship (with a cointegrating vector of (1 −1 −1)) between the government spending (inclusive of interest), taxation and seignorage variables.

Previous researchers have variously tested for cointegration between the variables including and excluding interest payments. Trehan and Walsh (1988) employ U.S. data to test both the restricted model and the unrestricted model when interest payments are included in the deficit. In each case they accept the hypothesis of a stationary deficit although in the unconstrained estimation the coefficient for their seignorage variable is not close to unity^[3]. Hakkio and Rush (1987) and MacDonald and Speight (1987) both test the unrestricted model employing the deficit excluding interest payments for U.S. and U.K. data respectively. Both accept the hypothesis of cointegration with coefficients close to unity. From the argument from Trehan and Walsh (1988) regarding inclusion of interest rates, and our argument relating the two hypotheses under the special condition of income growth and inflation outpacing interest rates, the two sets of results are invalid (as they do not allow for income growth the special condition cannot hold).

It is important to notice that if the primary deficit is financed by money creation, it is likely that the hypothesis of cointegration will be accepted. This is not an unlikely finding for Australia as it is only recently that the government has been able to determine the amount of debt that it issues. Prior to this, the institutional arrangements for issuing debt in Australia have involved the government setting the price while allowing the private sector to take up as much or as little as desired. That which was not purchased by the public resulted in increases in the holdings of debt by the Reserve Bank. Seignorage therefore became the residual financing instrument of the primary deficit in Australia over the sample period analysed in this paper. Figure 2 illustrates this point. Both the g_t (excluding interest payments) and (t_t+Δm_t) series follow very similar paths.

The second test is based upon Hamilton and Flavin's (1986) adaptation of Flood and Garber's (1980) test for hyper-inflationary bubbles to examine whether governments have resorted to bubble financing of their fiscal deficits. The test is derived from equation (2) above and reproduced below as equation (9).

This specification shows us that the level of debt outstanding at time t is equal to the sum of all future surpluses plus the present value of debt outstanding at time t=N. Taking expectations of the right hand side of this equation; the current level of debt is equal to agents expectations of future surpluses and their expectation of the amount of debt that will not be repatriated. In particular if

the present value of bonds held at time N is zero and the constraint holds. This does not preclude a positive holding of bonds in the limit (i.e B_N need not tend to zero as long as its present value does) which means that the government can continue to roll over debt so long as the debt is not increasing at a rate greater than (1+i)/(1+y) (1+p). The test is based on the existence of this term. If the limit of this is zero the term drops out of the equation (9) while if it is not, the bubble term will remain. Hamilton and Flavin (1986) show that if the limit approaches a constant then the alternative hypothesis is that

with a significant value for A₀ indicating that investors do not expect that the government will be able in the limit to repatriate all its outstanding debt.

It can be seen that the first term in equation (9)′ cannot be tested because we cannot measure the expected future path of the government surplus, both Hamilton and Flavin (1986) and MacDonald and Speight (1987) assume that current trends in the surplus will continue into the future. Whilst this does not constitute the full information set which investors consider in making expectations of future surpluses, this extrapolation is consistent with our test insofar as we are testing the hypothesis that current trends in government spending and financing decisions imply that the level of debt is too high. The expected surplus term can therefore appropriately be proxied in the present context by utilising an autoregressive representation of past surpluses. The expectations term was substituted out in the method of Hansen and Sargent (1981). For a lag length of one^[4]

This equation is estimated jointly with the autoregression of s_t

The bubble term in equation (11) is:

where A₀ is the coefficient to be estimated and t is a time trend. Considering the variable (1/δ^t) where δ is constant, the variable is a deterministic term integrated of order greater than one. The intuition of this result is that for (1+i)>(1+y) (1+p), (which must be the case if there is a constraint as in Hamilton and Flavin (1986)), then this term trends upwards over time. This term will pick up any deterministic trend in the bond series which is not accounted for by the surplus (including seignorage). The bond series in Hamilton and Flavin (1986) is stationary, which precludes the finding of a significant coefficient on the bubble term.

If i<y+p, the bubble term asymptotes to zero (the specification no longer tests for a bubble). The limit term can approach any value as 1/δ^t goes to zero as t increases. Thus a finding of a significant A₀ here is compatible with the hypothesis that the constraint is holding.

Once non-stationarity of the bond series is established, we can no longer make use of the usually applied t-statistic on the bubble term as it is no longer t distributed (Durlauf and Phillips (1986)), a point which is overlooked by Macdonald and Speight (1986)^[5]. An alternative to testing by the above method is necessary to determine whether or not the bubble term is correctly included in the model. Hall (1986) examines the inclusion of a variable in a cointegrating equation on the strength that its inclusion is necessary for white noise residuals to be obtained. Thus the method of testing is to test the restricted equation's residuals for stationarity (i.e. no bubble term). If the residuals remain stationary when the term is excluded then it is not significant. This can be applied by noting that when the series for bonds is integrated at a higher order than the fundamentals, then the residuals of the estimated equation (excluding the bubble term) will be non-stationary. If the inclusion of the bubble term results in an equation with stationary residuals then the bubble term is found to be correctly included and significant.

Footnotes

In this paper seignorage refers to financing the deficit by issuing money (inflation tax is treated separately). Even though the government may issue enough debt to finance a deficit, if this debt is taken up by the central bank then the effect is as if the central bank printed the money. [1]

The proof is lengthy and will not be reproduced here. [2]

The likely cause of this is that their seignorage variable is stationary. Their test for non stationarity accepts at the 10% level of significance. However, further tests using this variable show that its addition to a stationary variable results in a stationary variable. This is a contradiction to the original finding. [3]

Initially three lags were specified. Use of likelihood ratio tests for the full system resulted in acceptance of a lag length of one. [4]

These authors did not report any diagnostic checking of their final system of equations. What is likely is that the price level effects contained in the bond series is appearing in the equation through a significant deterministic trend (i.e the bubble term is significant). This may explain why they obtain results in conflict with their (possibly incorrect) cointegration results. [5]