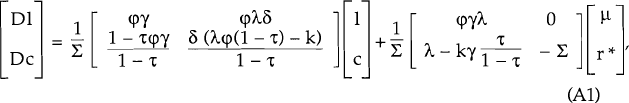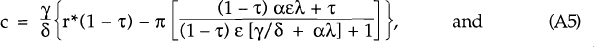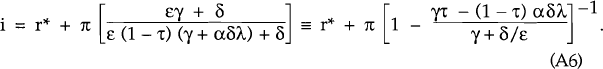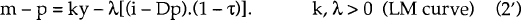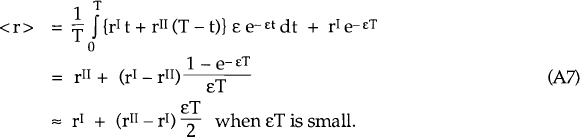RDP 9101: The Effect of Steady Inflation on Interest Rates and the Real Exchange Rate in a World with Free Capital Flows Appendix

1. Justification of a pre-tax international arbitrage condition: equation (1)

There are two relevant justifications – the first applies specifically to US citizens while the second is more general. A pre-tax arbitrage condition is relevant for US citizens because of the nature of the US tax system.^[22] US tax is levied on total world income – irrespective of the source of the income or its nature (e.g., interest income, or capital gain/loss^[23]). Thus, if US citizens have no liability for Australian withholding tax (for example, by investing in ‘widely held securities’ e.g., Euro $A raisings by Australian corporates^[24]) their investment decisions should depend on relative pre-tax rates of return and on perceived risk. The second justification for equation (1) is the tax treatment of many foreign superannuation funds. As well as being exempt from tax in their own countries, these funds have a general exemption from Australian income tax^[25]. The size of these foreign superannuation funds again suggests that pre-tax arbitrage conditions like equation (1) should be satisfied by Australian nominal assets.

2. The model when regime II involves ending nominal money growth with no jump in the level of the money supply

This model is more realistic than the one described in Section 3a of the text – but also more difficult to analyse. The system of equations (2) – (6) forms a set of two coupled differential equations:

where Σ = γ (φλ − k) − λ. Equation (A1) describes the evolution of the economy when it is not at equilibrium and when there is no future uncertainty. It may be expressed more compactly as:

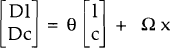where x is the vector of exogenous variables .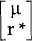

We assume that Σ < 0^[26] and that τφγ< 1. These assumptions both hold provided the slope of the Phillips curve, φ, is sufficiently small, i.e., provided inflation is sufficiently unresponsive to real activity. Using the notation, 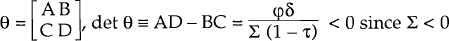. Hence,θ has a positive and a negative eigenvalue. The negative eigenvalue is 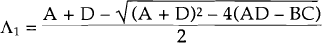(which is negative because AD − BC is negative). The eigenvector corresponding to this eigenvalue represents the stable path upon which the economy regains equilibrium.

Solving the equation, 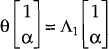, gives 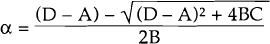. It follows from our assumptions (Σ < 0 and τφγ < 1), that B < 0, and BC > 0. As a consequence, α > 0. The equation for the stable eigenvector may alternatively be written,

where the superscript E again denotes the equilibrium value.

We now use Figure 5 to derive the solution of the model. Once regime II has been established, all uncertainty has been resolved and the economy evolves along the stable path [equation (A2) with 1^E = − λ (1 − τ) r^* and 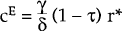]. This stable path is shown as the S'S line. While steady inflation (regime I) persists, the behaviour of the economy is determined by equations (2) – (4) and equation (6′), with “core inflation”, π, pre-determined, and the nominal interest rate, i, set by the monetary authorities to maintain “full employment” output. Equations (2) and (3) can be combined to give the relationship between c and 1 while steady inflation persists:

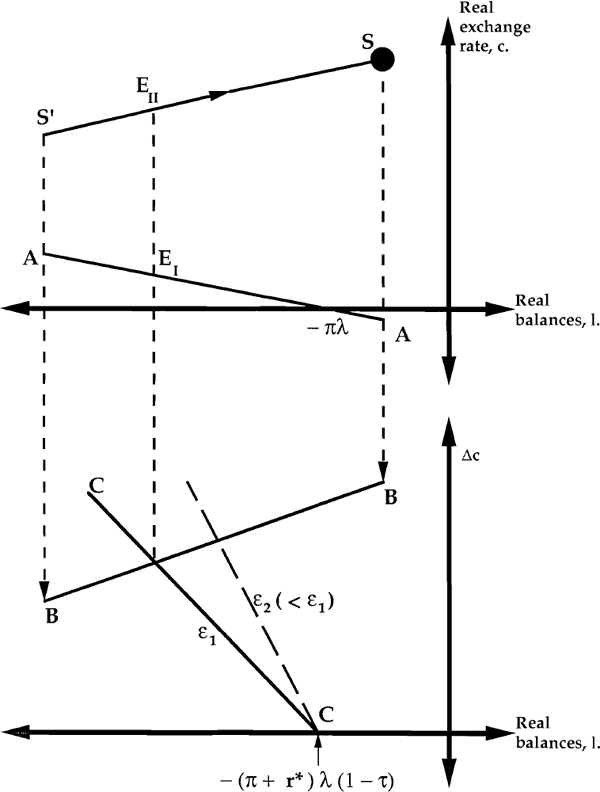
Equation (A3) is backward-sloping in c-1 space and is displayed by the line AA. When the regime change occurs, the economy jumps instantaneously from its equilibrium on the line AA to the stable path S'S. Given the structure of the economy, there is no jump in the level of real balances. Thus, we may derive the relationship between the jump in the real exchange rate, Δc, and the level of real balances when the jump occurs, 1. Given the slopes of AA and S'S, this relationship is upward-sloping in Δc−1 space, and is shown by the line BB. Finally, substituting equation (2) into the the international arbitrage condition (equation 6′), gives a second relationship between Δc and 1, namely,

which is backward-sloping in Δc−1 space, and is shown by the line CC. While regime I persists, equilibrium is determined by the intersection of BB and CC. Thus, while steady inflation persists, the economy sits at the point E_I in c-1 space. When the regime change occurs, the economy immediately jumps to E_II and then slowly evolves along the stable path to S.

Figure 5 also enables us to examine the effects of a change in ε. A fall in ε rotates the CC line clockwise around its 1-axis intercept (see equation A4). Therefore, iff Δc > 0 (or, equivalently, iff r > r^*), it leads unambiguously to an increase in Δc, and to a fall in the level of the real exchange rate, c – that is, to further over-valuation of the real exchange rate. Since in regime I, output is kept at its “full employment” level, there is a fall in the domestic nominal and real interest rate, so that the fall in the after-tax real interest rate offsets the output effect of the real appreciation.

Tedious but straightforward manipulation of equations (2), (3), (9), (10), (A2) and (A4) leads to these expressions for the level of the real exchange rate and the nominal interest rate while regime I persists:

It follows from equations (A5) and (A6) that .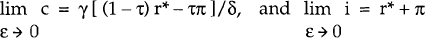

Thus, as the perceived probability of a regime change falls to zero, the model reverts to its ‘certainty’ version and the real pre-tax interest rate in the domestic economy reverts to the world real rate.

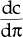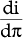Equation (A5) implies that is unambiguously negative. The first expression for i in equation (A6) implies that is unambiguously positive, while from the second expression it follows that, since 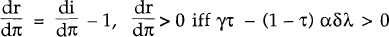. As the model contains seven parameters, an extensive search in parameter space is a major undertaking. Nevertheless, at least for plausible parameter values, 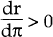. Thus, assuming these values for the parameters (see below for a brief justification): k = 1; 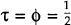; λ = 2; 1/ε = 5 years; δ/γ = 0.15; 1 ≤ “the multiplier” ≤3 implies .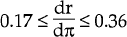

2a Parameter values

The values k = 1; 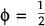and λ = 2 are used by Buiter and Miller (1982). We see no reason to change them. τ is the domestic tax rate on nominal income. 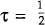is approximately the top marginal income tax rate in Australia. Especially since the introduction of full dividend imputation, this seems the appropriate tax rate to choose. 1/ε is the mean length of time for which the steady inflation regime is expected to persist. We choose 1/ε = 5 years.^[27] γ and δ are the parameters in the IS curve. The effect on output of changes in γ and δ can be analysed in terms of the “direct” effect on the components of output and the “multiplier” effect due to changes in (permanent) income inducing changes in consumption. We assume that the direct effect of a 1%p.a. permanent increase in the after-tax real interest rate is to reduce output by 1%. We assume that the price elasticity of both imports and exports is (see Gordon (1986) and Horton and Wilkinson (1989)). For Australia, both imports and exports are about 15% of GDP. Hence, the direct effect of a 1% depreciation of the real exchange rate is to increase output by 0.15%. Thus, δ/γ = 0.15. Finally, for the multiplier, we assume the range 1 ≤ “the multiplier” ≤ 3.

2b Results when taxation system is inflation-neutral

In this version of the model, to make the tax system entirely inflation-neutral requires eliminating the “inflation tax” on holdings of nominal money balances as well as taxing real income rather than nominal income. With the inflation tax eliminated, and inflation steady at rate π, the after-tax opportunity cost of holding money is (i − π).(1 − τ). Equation (2) then becomes

Solving this inflation-neutral model when there is no uncertainty (that is, solving equations 2′, 3′ and 4–6) leads to coupled differential equations analogous to equation (A1):

where x is the vector of exogenous variables 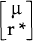, and θ′ is the matrix 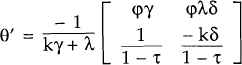. It fallows that det 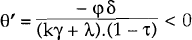, and hence θ′ has a single negative eigenvalue and this ‘inflation-neutral’ model is stable. The steady-inflation (regime I) equilibrium again satisfies equations (12′), (13′) and (14′). Thus, again, with an inflation-neutral tax system, the presence of inflation does not alter the equilibrium in the real economy.

3. The consequences had regime I been specified by the money growth rule μ = π

This specification leads to a more complex dynamic adjustment for the model. Even while regime I persists, in general during adjustment to a shock, De ≠ π. The correct form for the international arbitrage condition in regime I is then

Solving equations (2) – (5) and (6′′′) leads to a set of two coupled differential equations of the form: 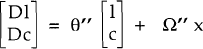where x is the vector of exogenous variables 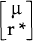, and det θ′′ = det θ + εφ (γ + αδλ)/Σ. Det θ′′ is unambiguously negative and so this version of the model is stable. While regime I persists, the adjustment to a shock (for example, an unanticipated permanent shock to ε) involves an instantaneous jump in the real exchange rate to put the economy onto the appropriate stable eigenvector of θ′′, after which the economy moves along this stable eigenvector towards the appropriate equilibrium point on the line AA in Figure 5. When the monetary regime changes from I to II, the economy jumps from this stable eigenvector to the stable eigenvector S'S. Thus, while regime I persists, the dynamic adjustment to shocks is more complex than the version of the model described in Part 2 of the Appendix.

4. Section 3 model when the relevant interest rate in the real economy is the expected average after-tax real rate over a time period of length T

This Part of the Appendix examines how the models in Section 3 are altered if the relevant interest rate in the real domestic economy at time t^* is the expected average after-tax real interest rate in the period t^*≤ t ≤ t^*+ T, rather than the short-term after-tax real rate at time t^*. For ease of notation, define the real after-tax interest rate in regime I as r^I (r^I ≡ i [1 − τ] − Dp) and in regime II as r^II (r^II ≡ r^* [1 − τ]). Then, while regime I persists, the expected average real after-tax interest rate over a time period of length T, <r>, isthe equilibrium is again given by

Then, equation (3) should be replaced by

where <r> is given by equation (A7). It follows that, while steady inflation persists, the equilibrium is again given by equations (12), (13) and (14) but with 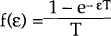replacing ε. Since 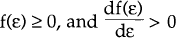, this specification makes no qualitative difference to the results.

The regime I equilibrium continues to be characterized by a domestic short-term pre-tax (after-tax) real interest rate higher (lower) than the comparable world rate, and by an over-valued domestic real exchange rate.

Footnotes

This information was kindly supplied by the Internal Revenue Service Section of the US Consulate in Sydney on 15 March, 1990. [22]

There is one relevant complication: a maximum of $US 3,000 per annum capital loss can be written off against other income for US tax-payers. For large investors, this may be a significant distortion. However, in a diversified portfolio which includes assets from several countries, a capital loss on holdings in one currency can be offset against capital gain on holdings in other currencies. This should reduce the distortion, though not eliminate it. [23]

Section 128F, Income Tax Assessment Act 1936 (personal communication, Mr. Will Duda, Australian Tax Office). [24]

Section 23(jb), Income Tax Assessment Act 1936 (personal communication, Mr. Will Duda, Australian Tax Office). [25]

Buiter and Miller (1981) give a justification for this assumption. [26]

Assuming all the other parameter values unchanged and 1/ε = 10 years, implies 0.11 ≤ dr/dπ ≤ 0.23. [27]