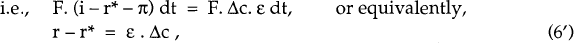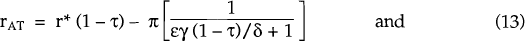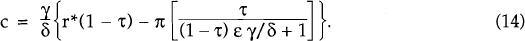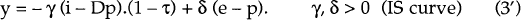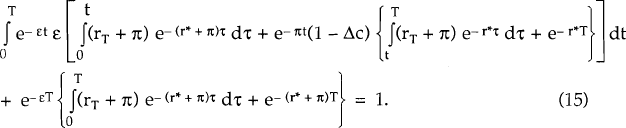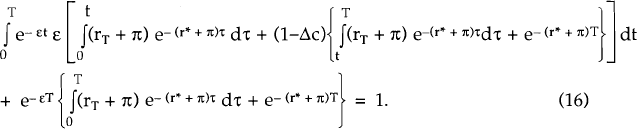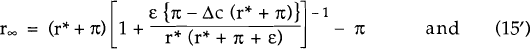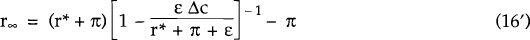RDP 9101: The Effect of Steady Inflation on Interest Rates and the Real Exchange Rate in a World with Free Capital Flows 3. Introducing Uncertainty

3a The possibility that steady inflation will end

Countries with relatively high inflation face a dilemma not shared by countries with relatively low inflation. When inflation is low, there is general agreement that it should be kept low. When inflation is relatively high, there is no comparable consensus. Some argue that even moderate steady inflation is sufficiently costly that it must be eliminated quickly. Others counter that the output costs of eliminating inflation are themselves sufficiently high that they outweigh the benefits of lower inflation. While relatively high inflation persists, even when it is steady, there are continual calls for it to be reduced.^[12]

Thus, when a country runs inflation, even steady inflation, at a rate significantly higher than its trading partners, it is unrealistic to assume that this inflation will never be reduced. Importantly, dropping this assumption changes the nature of the equilibrium – as we now demonstrate. Assume instead that there are two possible monetary policy regimes. Initially, the domestic economy is in equilibrium with steady inflation, π(π > 0), and the monetary authorities set the nominal interest rate, i, to maintain this steady inflation at “full employment” output. This is regime I. The second monetary policy regime (regime II) involves an immediate ending of nominal money growth coupled with an increase in the level of the money supply sufficient to allow the economy to instantly jump to its new long-run equilibrium.^[13] When the monetary policy regime changes from I to II, we assume that it is immediately credible and expected to be permanent.^[14] Thus, after the regime change, all uncertainty has been resolved, and the economy immediately jumps to the equilibrium defined by equations (7) – (10) with π = 0.

We assume that while the first (steady inflation) regime persists, agents assess the probability of a regime change occurring in the next infinitesimal time interval dt as ε dt.^[15] We now derive the appropriate international arbitrage condition for regime I.

In equilibrium with the domestic economy inflating steadily at rate π, the nominal exchange rate depreciates steadily at rate π, so that the real exchange rate remains unchanged. Hence, the excess return earned over an infinitesimal time interval dt by a foreigner holding all her wealth, F, in short-term domestic nominal assets rather than comparable foreign assets is F. (i − r^* − π) dt.

In general, when the monetary policy regime change occurs, there is a jump in the real exchange rate, Δc, because uncertainty has been resolved. When the jump occurs, the capital loss to our foreigner if she is holding all her wealth in domestic short-term nominal assets, is F. Δc.^[16] Since, by assumption, foreign investors are risk-neutral, the expected excess return from investing in domestic assets must be zero,

where, as before, r is the domestic short-term pre-tax real interest rate.

We may now derive the equilibrium. While steady inflation persists, the real exchange rate, c, satisfies equation (3) at full-employment output (y ≡ 0). When regime II is established, the real exchange rate jumps to its zero-inflation equilibrium level, 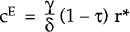. Therefore, the jump in the real exchange rate, Δc, when regime II is established is,

Solving equations (6′) and (11) gives,

Thus, while steady inflation persists, the domestic pre-tax real interest rate, r, exceeds the world pre-tax real interest rate, r^*, while the domestic after-tax real interest rate is lower than it would be if there was no domestic inflation. The real exchange rate is over-valued. The higher the level of steady inflation, the higher the domestic pre-tax real interest rate, the lower the after-tax real interest rate and the more over-valued the real exchange rate.

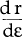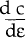It follows from equations (12) and (14) that both and are unambiguously positive. Thus, an increase in the perceived probability of inflation coming to an end shifts the steady inflation equilibrium to a higher domestic real interest rate (both pre-tax and after-tax) and a less over-valued real exchange rate.

3b The possibility that an inflation-neutral tax system or a real interest equalization tax will be introduced

Introducing an inflation-neutral tax system involves taxing real income rather than nominal income. With inflation steady at rate π, and an inflation-neutral tax levied at rate τ, the after-tax real interest rate is r_AT = (i − π).(1 − τ). Equation (3) then becomes:

Even while steady inflation continues, upon introduction of such a tax system (and the associated adjustment of the nominal interest rate to keep output at its full employment level) the equilibrium in the real economy is characterised by

Thus, not surprisingly, introducing an inflation-neutral tax system leads to the same equilibrium in the real economy as is achieved by eliminating inflation.

A real interest equalization tax^[17] is designed to eliminate the real interest premium earned by foreigners investing in domestic nominal assets. It involves imposing a tax, Θ, on foreign lenders with Θ = r − r^*. Equation (6′) becomes

Upon imposition of such a tax (and the associated adjustment of the nominal interest rate to keep output at its full employment level) the equilibrium is characterised by

with r_AT and c again given by equations (13′) and (14′).

Thus, we may re-interpret the model of Section 3a as follows. Redefine regime II as a permanent and immediately credible introduction of either an inflation-neutral domestic tax system or a real interest equalization tax combined with a continuation of nominal money growth at rate μ = π.^[18] The introduction of either of these versions of regime II leads to the same capital loss on short-term nominal assets as in the Section 3a model. As a consequence, while regime I persists, the equilibrium in the real economy is again given by equations (12) – (14).

3c The yield curve

By assumption, there is no uncertainty in the world economy and hence the world interest rate on nominal securities with any maturity is r^*. For the Section 3a model, the domestic nominal exchange rate depreciates at rate π until the regime change occurs, when there is a jump depreciation of magnitude Δc, followed by no further nominal depreciation (because domestic inflation has ceased). Hence, while regime I persists, the appropriate arbitrage condition for a domestic security which pays nominal interest at rate i_T (i_T ≡ r_T + π) over the time interval 0 ≤ t ≤ T and is then redeemed at T for one unit of domestic currency is:

The probability that the regime change will occur between times t and t + dt is e^−εT ε dt, and the term in square brackets is the present discounted value of the security if the regime change occurs at time t, 0 ≤ t ≤ T. The probability that the regime change will not occur over the time interval 0 ≤ t ≤ T, is e^−εT.

For the Section 3b models, steady domestic inflation continues after the regime change and hence so does the steady nominal depreciation of the domestic exchange rate. Hence, while regime I persists, the appropriate arbitrage condition for a domestic nominal security with a life of T is:

Both equations (15) and (16) lead to complicated expressions with little intuitive appeal. However, in the limit as T → ∞, the expressions reduce to:

There are several notable features of these equations. To begin, consider the case when steady inflation is expected to continue after the regime change (i.e., the Section 3b models for which the relevant equations are (16), (16′) and (16′′)). Then, while regime I persists, holders of infinitely-lived domestic securities demand a real interest rate higher than the world real interest rate (equation (16′) implies that r_∞>r^*). However, they do not require an interest rate as high as the short-term interest rate (equation (16′′) implies that r_∞− r^*< εΔc = r − r^*).

Intuitively, this can be understood as follows. Over each short time interval while regime I persists, foreign holders of short and infinitely-lived domestic securities face the same expected capital loss – arising from the possibility of a regime change. Hence, they both require a real return higher than the world interest rate. However, holders of short-term securities require a higher interest rate than holders of infinitely-lived securities because, unlike the former, the latter have locked-in a favourable interest rate for the infinite life of their security.

In the case when steady inflation is expected to end after the regime change (i.e., the Section 3a model), the relevant equations are (15) and (15′). Holders of infinitely-lived domestic securities now receive a further compensation not available to holders of short-term securities.

After the regime change occurs, the steady nominal depreciation of the domestic currency ends – which increases the real yield on infinitely-lived securities. If π > Δc (r^* + π), this effect is so important that, while regime I persists, r_∞< r^*.

To summarize, both the Section 3a and Section 3b models imply that, while regime I persists, the domestic yield curve will be inverse. Figure 4 provides some empirical model estimates for the domestic yield curve using plausible parameter values. Based on Table 1, the calculations assume: r^* = 5%p.a., r − r^* = ε Δc = 2.5%p.a. and π = 4%p.a. (roughly the inflation difference between Australia and the ‘large four’ over the six years). The average duration of regime I is 1/ε and I examine two possible values: 1/ε = 5 years (hence Δc = 12.5%) and 1/ε = 10 years (hence Δc = 25%).

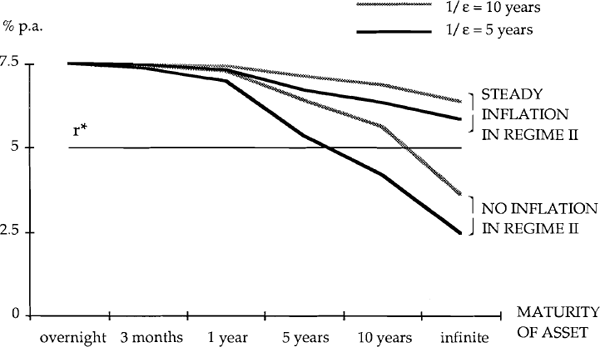
The long-term Australian government bonds used in Figure 2 and Table 1 are 10 year bonds. Using the above parameter values, the models predict a domestic real interest rate on 10 year bonds of r_10year − r^* = − 0.8%p.a. or 0.6%p.a. when regime II has no inflation and 1/ε = 5years or 1/ε = 10 years and r_{10 year} − r^* = 1.3%p.a. or 1.8%p.a. when regime II has steady inflation and 1/ε = 5 years or 1/ε = 10 years. The real interest differential between Australian 10 year bonds and ‘large four’ long-term bonds has fluctuated around zero (see Figure 2) and has averaged 0.9%p.a. over the period under study (see Table 1). While this comparison is far from definitive, the prediction from the models that the yield curve should be strongly inverse seems consistent with the Australian experience of the past six years.^[19]

Footnotes

This asymmetry between the policy choices facing countries with high and low inflation rates has recently been invoked to explain why high inflation raises inflation uncertainty (Ball, 1990). An alternative possible source of uncertainty is a belief in the market that the monetary authorities might, at least temporarily, give up the fight against inflation and loosen monetary policy. This possibility is examined in footnote 19. [12]

In the new zero-inflation equilibrium, the opportunity cost of holding money is smaller and hence the demand for money is larger. From equation (9), the required increase in the level of the money supply is Δm = λ(1 − τ)π. See Buiter and Miller (1981) for further discussion. [13]

It is difficult to imagine that regime II, as described, would be immediately credible. The specification chosen simplifies the analysis. In Part 2 of the Appendix, we specify regime II without the step increase in the level of the money supply. Note that the nominal interest rate is the monetary policy instrument in regime I, while regime II involves a monetary target. Again, this simplifies the analysis. In Part 3 of the Appendix, we briefly deal with the version of the model in which regime I is specified in terms of steady money growth at rate μ = π. [14]

If ε is constant over time, the probability that the regime change does not occur over a time interval of length T is e^−εT. On average, regime I persists for the length of time 1/ε. Note that this specification implies that the steady inflation regime (regime I) must eventually end. However, it is easy to extend the model to the case where investors think that there is a probability 1−q (0 < q < 1) that regime I will continue forever. The probability of a regime change occurring in the next infinitesimal time interval dt is then q.ε dt rather than ε dt. All results are as in the text, with q ε replacing ε. [15]

We use the common approximation that, for small x, ln(1 + x) ≈ x, where x is the proportionate change in the real exchange rate. Assuming all interest rates are short-term avoids dealing with the change in the capital value of outstanding long-term bonds when the monetary policy regime changes. See Section 3c for the implications of the model for longer-term interest rates and Part 4 of the Appendix for a plausible alternative specification. [16]

Liviatan (1980) and Dornbusch (quoted in Buiter and Miller (1981)) suggested a real interest equalization tax in the context of reducing inflation in a world with free global capital flows. The analysis here suggests that their argument also applies in an economy which must run short-term real interest rates higher than comparable world rates to keep inflation steady. [17]

As in Section 3a, to allow an immediate jump to the long-run equilibrium it is also necessary to have a step change in the level of the money supply. [18]

We are now in a position to examine the possibility that the market believes that the monetary authorities might, at least temporarily, give up the fight against inflation and loosen monetary policy – thereby leading to an immediate fall in the exchange rate. As before, this possibility would lead the market to require a real interest premium on domestic short-term nominal assets. But, as should be clear from the above analysis, it also implies that the yield on domestic longer-term assets should be higher than the yield on short-term assets – to provide compensation for the possibility of higher inflation in the future. We can therefore conclude that market anticipation of such a possibility cannot explain both high short-term real rates and lower longer-term real rates in Australia over the last six years. [19]