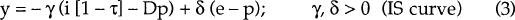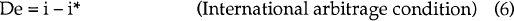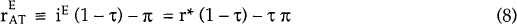RDP 9101: The Effect of Steady Inflation on Interest Rates and the Real Exchange Rate in a World with Free Capital Flows 2. The Model when the Future is Certain
February 1991
- Download the Paper 384KB
We analyse a modification of the model introduced by Buiter and Miller (1981). The main modification is to include a tax system which is not inflation-neutral. The model provides a simple description of a small open economy in a world of floating exchange rates and perfect capital mobility. Accepting the arguments presented in the introduction, we assume that risk premia are small enough to be ignored, and that world investors base their investment decisions on expected pre-tax rates of return. The log-linear equations of our model are:
List of symbols
| m | logarithm of the nominal money stock |
| P | logarithm of the domestic price level |
| y | logarithm of real domestic output (zero represents “full employment” real output) |
| i | domestic nominal short-term interest rate on non-money assets[10] |
| i* | world nominal short-term interest rate on non-money assets |
| r | domestic pre-tax short-term real interest rate (r ≡ i – Dp) |
| r* | world pre-tax short-term real interest rate |
| e | logarithm of the nominal exchange rate (domestic currency price of foreign currency) |
| D | the differential operator, so, for example, Dp ≡ dp/dt. |
| π | “core” rate of domestic inflation |
| μ | rate of growth of the domestic nominal money supply; μ = D+m where D+m is the right-hand side derivative of m(t): D+m(t) ≡ lim {[m(t+h) – m(t)]/h},h > 0. h→0 |
| τ | domestic tax rate, assumed to apply equally to nominal income earned by individuals and companies; 0 < τ < 1 |
| 1 | logarithm of domestic real balances (l ≡ m − p) |
| c | logarithm of the domestic real exchange rate (c ≡ e − p). |
A short description of the model follows. The demand for real balances (equation 2) increases with the level of real activity in the economy and falls with the after-tax opportunity cost of holding money. The level of real activity (equation 3) depends negatively on the after-tax real interest rate, and positively on the real exchange rate. We assume that there is no foreign inflation, so that the world nominal and real interest rates are equal (i* = r*). Without loss of generality, we assume that the logarithm of the world price level is equal to zero and so the log of the domestic real exchange rate is c (c ≡ e − p). Note that, as defined, a fall in the real exchange rate corresponds to a real exchange rate appreciation. Domestic inflation is generated by an expectations-augmented Phillips curve (equation 4), with “core” inflation determined by the expected future growth of the nominal money supply (equation 5). The exchange rate is determined by rational forward-looking risk-neutral agents who understand the structure of the economy as well as the parameters of the model. They ensure that expected rates of return on foreign and domestic nominal assets are equalized (equation 6). Equation (6) is equivalent to equation (1) with the risk premium, rp, set to zero.
Following Buiter and Miller, we assume in this Section of the paper that the forward-looking agents in the foreign exchange market expect the domestic nominal money supply to continue to grow at rate μ forever, and hence expect domestic inflation at rate π (π = μ) to continue forever. In equilibrium, Dl = Dc = 0, and these conditions allow the equilibrium domestic levels of interest rates, real balances and the real exchange rate to be derived:
where the superscript E denotes equilibrium and the subscript AT denotes after-tax. Note that the international arbitrage condition (equation 6) ensures that in equilibrium, the domestic pre-tax real interest rate is equal to the world pre-tax real interest rate (equation 7). This fact, together with a domestic tax system which is not inflation-neutral implies that the domestic real after-tax interest rate is a decreasing function of domestic inflation (equation 8). In equilibrium, output is at its full-employment level. Since output is a function of the real aftertax interest rate and the real exchange rate (equation 3) it follows that the equilibrium real exchange rate is also a function of the rate of domestic inflation (equation 10). The higher the level of steady domestic inflation, the more over-valued the real exchange rate.[11]
Intuitively, this result can be understood as follows. A lower after-tax real interest rate increases domestic demand – and, in particular, increases demand for domestic non-traded goods. For the non-traded goods market to continue to clear, it is necessary for there to be an increase in the relative price of non-traded goods – that is, an appreciation of the real exchange rate.
Footnotes
In the model in this Section, there is no future uncertainty and no distinction between short and long interest rates. However, as we shall see, assuming all interest rates are short-term simplifies the analysis in Section 3. [10]
As defined, a low level of c corresponds to an over-valued real exchange rate. [11]