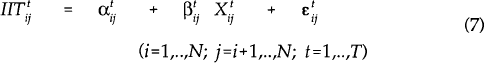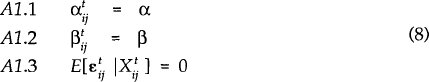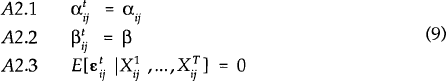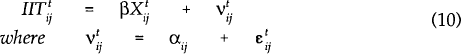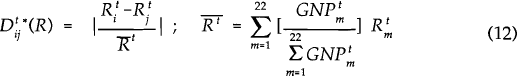RDP 9110: Resource Convergence and Intra-Industry Trade 4. Empirical Tests of Intra-Industry Trade Models
November 1991
- Download the Paper 384KB
In this section we turn to testing the propositions discussed in Section 3. We conduct tests on two different data sets. The first uses the time series on the share of intra-industry trade in total intra-OECD trade. The second examines the importance of intra-industry trade in bilateral trade by using both cross section and time series data. The tests use data for the period 1965–85.
Propositions 1 and 3(a) suggested that the share of intra-industry trade in the within group volume of trade should be negatively correlated with resource dispersion and positively correlated with economic size. These propositions are tested by regressing the share of intra-industry trade in total intra-OECD trade on the weighted coefficient of variation for each resource ratio and on the log of OECD aggregate GDP (the coefficient of variation for the land/labour ratio is excluded as it is essentially constant). The results are reported in column (1) of Table 5.
| 1 | 2 | 3 | |
|---|---|---|---|
| LAG OF INTRA- INDUSTRY TRADE SHARE |
0.23 (1.27) [1.91] |
||
| TIME TREND | −0.62 (2.66) [3.33] |
−0.37 (1.88) [3.94] |
|
| DISPERSION OF CAPITAL/LABOUR RATIOS |
−52.62 (6.17) [10.80] |
−28.63 (2.48) [4.28] |
−23.52 (2.22) [3.45] |
| DISPERSION OF SKILLED LABOUR RATIOS |
−12.95 (0.87) [1.17] |
−15.90 (1.26) [2.07] |
−16.76 (1.75) [2.58] |
| DISPERSION OF NAT. RES./ LABOUR ENDOWMENTS |
−16.74 (2.52) [5.41] |
−18.38 (3.23) [4.80] |
−17.16 (3.75) [6.34] |
| LOG OF TOTAL OECD GDP |
10.72 (4.26) [6.96] |
34.53 (3.76) [4.93] |
22.52 (2.63) [5.79] |
 |
0.97 | 0.98 | 0.98 |
NOTES |
|||
Each of the coefficients on the three resource variables has the expected negative sign, with the coefficients on the dispersion of capital/labour ratios and natural resources/labour ratios being highly significant. This result provides support for Proposition 1 above. The log of OECD GDP also has the expected positive sign. This supports the view that as a group of countries becomes larger in terms of the size of their economies, economies of scale can be more widely exploited with a resulting increase in trade in differentiated products.
Each of the exogenous variables shows some evidence of trending through time. Given the nature of these variables we assume that they are trend stationary rather than characterized by a martingale process with drift. In this case ordinary least squares ensures stationarity of the errors but does not ensure that the residuals are orthogonal to all the regressors. To overcome this difficulty we include a time trend in the regression. The results are reported in column (2). Qualitatively, they are the same as those reported in column (1). The three resource dispersion indices have negative coefficients and the size variable a positive coefficient. The coefficients on skilled labour and mineral resources are essentially unchanged while the coefficient on the capital/labour ratio is reduced by nearly 50 per cent.
The estimated equation is a static relationship. We might expect that the impact of changes in resources on trade patterns would not always be completed within the year. The standard errors reported in square brackets are robust to the serial correlation that this slow adjustment may induce. It is of interest, however, to estimate the dynamic effects of changes in resource dispersion on the structure of international trade. Unfortunately, the limited amount of data restricts us to very simple specifications. In column (3) we report the estimation results when the lagged value of intra-industry trade is included in the estimated equation. Again, the results are qualitatively the same as those in columns (1) and (2). In fact the estimated coefficients do not change substantially from those in column (2). The coefficient on the lagged value of intra-industry trade is positive, with a significance level of 0.07. The relatively small size of the coefficient suggests that much of the adjustment in trade patterns is completed within the year. Further work on the dynamic effects, however, awaits longer time series.
We turn now to an examination of bilateral intra-industry trade. In all there are 231 different bilateral trading pairs in the sample. Data for each of these pairs are used for the years 1965–1985. Pooling the cross section and time series observations there are 4851 observations. As discussed above, theory provides little guide as to the precise specification of the equation to be estimated or to the appropriate estimation technique. Consequently, we use a number of different specifications and estimation techniques to ensure the robustness of our results.
The most general specification is:
where 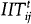 is
the share of intra-industry trade in total trade between countries i and j in
year t and
is
the share of intra-industry trade in total trade between countries i and j in
year t and 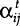 is an unobservable trading pair, time specific
effect. Restrictive assumptions are necessary before this equation can be estimated. The most
restrictive set of assumptions that we consider are the following:
is an unobservable trading pair, time specific
effect. Restrictive assumptions are necessary before this equation can be estimated. The most
restrictive set of assumptions that we consider are the following:
Under these assumptions pooled OLS, using all 4851 observations, is the appropriate estimation technique.
One of the benefits of pooling time-series and cross-section data is the ability to control for unobservable individual trading pair specific effects. Such factors as peculiar historical relationships or similar cultures may affect the level of integration of two economies and thus the importance of intra-industry trade. In this case we relax the assumption of a common intercept for all trading pairs but maintain the time invariant assumption. Thus:
If we assume that the trading pair effects are not correlated with the observable explanatory variables the model can be re-written as:
In this case the generalized least squares (GLS) estimator is the appropriate estimator. If
instead the specific effects are correlated with the observable independent variables GLS yields
biased and inconsistent parameter estimates. In this case the appropriate procedure is to
estimate the model with a different intercept for each trading pair. This estimator is known as
the “fixed effects” (or “within”) estimator (see Hausman and Taylor (1981)). Note that in contrast to the pooled OLS estimator the
GLS and fixed effects estimators require strict exogeneity of the 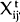 .
.
In the above specifications we have assumed that the parameters are constant through time. This need not be the case. If there are no specific trading pair effects or the effects are uncorrelated with the independent variables, estimation can be conducted period by period.
Below are reported estimation results under each of the above assumptions. All estimation is carried out under the further assumptions of homoskedasticity and no serial correlation. Hypothesis tests for the fixed effects and the pooled OLS estimates are, however, conducted using covariance matrices which are robust to serial correlation and heteroskedasticity. These covariance matrices are estimated using a panel data extension of the Newey and West (1987) estimator. We allow for unrestricted heteroskedasticity and serial correlation within the residuals for each trading pair but assume that the residuals across trading pairs are independent. Two autocovariances are allowed to be non-zero.
In order to test the propositions concerning differences in factor compositions on bilateral intra-industry trade it is necessary to define measures of the degree of dispersion in two country's resource endowments. Again theory provides little guide. To ensure that the results are not sensitive to the measure chosen we use two different measures of dispersion. These are defined below:
where 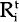 is
the ratio of resource R to labour in country i at time t. The higher
either index the greater the difference between the two countries relative endowments of the
resource. The results were not sensitive to the index chosen. Below we report results for the
is
the ratio of resource R to labour in country i at time t. The higher
either index the greater the difference between the two countries relative endowments of the
resource. The results were not sensitive to the index chosen. Below we report results for the
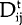 (R) index.
(R) index.
As discussed above the size of an economy may influence the amount of intra-industry trade that occurs. To test this proposition for bilateral trade flows both the log of the larger country's GDP and the log of the smaller country's GDP are included. If size affects the extent of intra-industry trade by allowing exploitation of economies of scale in a greater number of industries it should be the size of the smaller country which is the more important determinant of intra-industry trade.
If two countries share a common border, economic integration is likely to be more extensive and thus the share of intra-industry trade in total trade may be higher. A dummy variable which takes the value of one if the two countries have a land border and zero otherwise is included in the estimated equation. Also included is an EEC dummy which takes on a value of 1 if both countries are members of the EEC. As before a number of the variables are trending through time. Accordingly, we report estimates both including and excluding a time trend.
Table 6 reports the estimation results under the various assumptions. The first 2 columns report the estimation results under assumptions A1.1–A1.3. The results again provide support for intra-industry trade models. This finding does not depend upon the inclusion/exclusion of a time trend.[6] Three of the four resource variables have significant negative signs as the theory predicts. The greater the difference in two countries' capital/labour ratios, land/labour ratios and skilled labour ratios the smaller is the share of intra-industry trade in the two countries' bilateral trade. The results suggest that the reverse is true for the natural resources/labour ratio. This variable, however, plays relatively little independent role in influencing the importance of intra-industry trade amongst the OECD nations.
| βPOOLED | βBW | βFE | βGLS | ||||
|---|---|---|---|---|---|---|---|
| TIME TREND | 0.06 (2.26) [2.27] |
0.51 (14.15) [13.91] |
0.31 (12.67) |
||||
| CAPITAL/LABOUR RATIO | −40.70 (11.49) [12.95] |
−40.05 (11.27) [12.65] |
−42.91 (2.64) [3.06] |
8.12 (2.05) [1.86] |
2.74 (0.70) [0.66] |
−0.91 (0.23) |
0.33 (0.09) |
| SKILLED LABOUR RATIO | −35.18 (8.21) [8.53] |
−34.93 (8.16) [8.49] |
−39.94 (2.04) [2.16] |
28.01 (5.51) [4.62] |
18.89 (3.76) [3.24] |
16.83 (3.40) |
15.74 (3.22) |
| NAT. RES./LABOUR RATIO | 4.59 (5.02) [4.76] |
4.46 (4.87) [4.62] |
7.39 (1.63) [1.55] |
−4.94 (7.16) [6.47] |
−3.81 (5.59) [5.03] |
−4.28 (6.01) |
−4.03 (5.84) |
| LAND/LABOUR RATIO | −25.18 (19.67) [20.24] |
−24.84 (19.27) [19.77] |
−26.06 (4.68) [4.89] |
−32.37 (4.47) [4.22] |
−5.75 (0.78) [0.73] |
−30.06 (7.18) |
−13.85 (3.17) |
| LN(YMAX) | 0.79 (5.22) [5.27] |
0.77 (5.08) [5.14] |
0.79 (1.20) [1.23] |
1.10 (1.73) [1.59] |
−5.58 (7.11) [6.45] |
1.51 (3.30) |
−1.12 (2.24) |
| LN(YMIN) | 6.39 (30.41) [33.33] |
6.29 (29.38) [30.16] |
6.42 (6.97) [7.43] |
11.08 (16.07) [14.88] |
4.05 (4.82) [4.69] |
9.49 (18.77) |
4.86 (7.82) |
| BORDER | 17.98 (31.24) [25.75] |
18.06 (31.33) [25.84] |
17.70 (7.16) [5.88] |
19.36 (8.12) |
22.51 (9.37) |
||
| EEC | 7.57 (19.78) [18.91] |
7.59 (19.83) [19.02] |
7.60 (4.64) [4.54] |
6.88 (4.25) |
7.90 (4.86) |
||
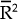 |
0.523 | 0.524 | 0.545 | 0.282 | 0.287 | 0.310 | 0.309 |
| No. Obs. | 4851 | 231 | 4851 | 4851 | |||
| TEST-NL | 0.04 {0.84} |
0.04 {0.84} |
TEST: βBW=βFE | 104.19 {0.00} |
|||
1. A constant (not reported) was also included in all equations
except for the “fixed effect” equation. |
|||||||
The parameter estimates suggest that if a country has three times as much capital per worker as a trading partner the share of intra-industry trade in their bilateral trade would be 7 percentage points lower than if the capital/labour ratios were identical. The impact of a similar 3:1 difference in the skilled labour ratio is slightly smaller while a 3:1 difference in the land/labour ratio would result in an approximately 4 percentage point decline in intra-industry trade compared to the level if the ratios were identical.
Both the size variables have significant positive coefficients with the coefficient on the size of the smaller country being significantly larger than that on the size of the larger country. While the coefficient on the size of the larger partner is statistically significant it does little to explain the variation in the extent of bilateral intra-industry trade. Increasing the size of the larger country from 25 per cent of the OECD average to the OECD average increases intra-industry trade by just 2.2 percentage points. In contrast increasing the size of the smaller country by the same amount increases intra-industry trade by approximately 10.5 percentage points. This provides support for Proposition 3(b).
The coefficients on both the Border and EEC dummies are positive and significant. The existence of a land border between two countries is an important determinant of the extent of intra-industry trade. After controlling for resource differences and size, the existence of a land border increases the share of intra-industry trade by approximately 18 percentage points. Membership of the EEC increases the share of intra-industry trade by a further 7 to 8 percentage points.
The theory provides little guide as to the functional form of the equation to be estimated. The relationship between the dispersion indices and intra-industry trade is conceivably non-linear. Under the null hypothesis that the specification is correct:
where X represents the independent variables included in the estimated equation and W all other
variables. Under the null, all functions of the form θ(W,π) should be orthogonal to the
residuals 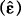 and thus:
and thus:
An obvious test for nonlinearity is to test this orthogonality assumption for various functions
of X and β. Of the many possible candidates we report results for 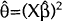 (TEST-NL
in Table 6). The reported test is a standard LM test and is robust to heteroskedasticity and
serial correlation. The results indicate that the orthogonality condition cannot be rejected.
Broadly similar results were found using other functional forms. These tests suggest that the
support for the intra-industry trade model does not rest on the linearity assumption.
(TEST-NL
in Table 6). The reported test is a standard LM test and is robust to heteroskedasticity and
serial correlation. The results indicate that the orthogonality condition cannot be rejected.
Broadly similar results were found using other functional forms. These tests suggest that the
support for the intra-industry trade model does not rest on the linearity assumption.
The third column presents the results using the “between” estimator (βBw).This estimator removes all time series variation from the data by taking the time average of all the variables. The sample size is thus 231. The results are broadly similar to those in the first 2 columns.
We now explicitly allow for trading pair specific effects. The fixed effects estimates are reported in columns 4 and 5. Unlike the earlier results they provide only weak support for the theory. While the natural resources and land variables have the theoretically correct sign, both the capital and skilled labour variables have the incorrect signs. This result is unchanged by the inclusion of a time trend, although the coefficient on the capital/labour becomes insignificantly different from zero. These results suggest that, at the level of bilateral trade, changes in resource endowments do not do particularly well in explaining changes in intra-industry trade over time. The results using the GLS estimator, which includes the specific effects in the error structure rather than as constants, are similar to the fixed effects results.[7] The table also reports the results of a Hausman specification test of the null hypothesis that βBW=βFE. The hypothesis is overwhelmingly rejected.
There are a number of possible explanations for these poor results. An examination of Table 3 shows that the variation in intra-industry trade across nations is considerably greater than the variation across time in individual countries. The fixed effects estimator does not make use of this variation in mean levels across countries. Instead, it uses the smaller variation across time. In contrast, the between estimator uses the variation in mean levels across countries ignoring any time variation. Other possible explanations for the poorer results in the time domain are the susceptibility of the fixed effects estimator to errors in variables and the difficulty of capturing the correct dynamics.
The above estimations were conducted under the assumption that the parameter estimates are constant through time. Previous work by Helpman (1987) questions the validity of this assumption. Hence, we estimate the equation using each year as a separate cross section. The results for selected years are shown in Table 7. While a number of the parameter estimates appear to be trending through time it is not possible to reject the null hypothesis that the parameters are constant through time (TEST1). It is, however, possible to reject the null hypothesis that the coefficients are the same in 1965 and 1985 (TEST2).
| Capital | Skill | Land | Natural | Ymax | Ymin | Border | EEC | 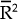 |
JPN | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1965 | −14.88 [1.27] |
−35.82 [2.41] |
−20.65 [4.90] |
7.87 [2.09] |
0.68 [1.25] |
6.95 [8.30] |
15.56 [5.63] |
4.92 [3.04] |
0.54 |
−3.07 [1.99] |
| 1967 | −26.84 [2.21] |
−33.36 [2.88] |
−21.65 [4.39] |
5.23 [1.30] |
0.69 [1.19] |
6.72 [7.69] |
15.17 [4.97] |
6.29 [3.40] |
0.52 |
−0.26 [0.15] |
| 1969 | −30.34 [2.59] |
−32.13 [1.95] |
−23.11 [4.32] |
2.62 [0.60] |
0.49 [0.75] |
6.82 [7.27] |
17.11 [5.62] |
6.04 [3.15] |
0.50 |
−1.09 [0.59] |
| 1971 | −35.58 [2.57] |
−35.29 [1.77] |
−24.85 [4.38] |
6.73 [1.57] |
0.57 [0.86] | 7.21 [7.73] |
17.49 [5.82] |
6.24 [3.58] |
0.52 |
−1.27 [0.52] |
| 1973 | −30.16 [2.59] |
−47.07 [2.68] |
−26.22 [4.79] |
4.73 [1.07] |
0.60 [0.89] |
6.90 [7.56] |
17.46 [6.04] |
7.15 [4.05] |
0.53 |
−3.30 [1.71] |
| 1975 | −37.48 [2.46] |
−44.30 [2.27] |
−28.53 [5.08] |
8.75 [2.08] | 0.79 [1.13] |
6.28 [6.63] |
18.95 [6.20] |
8.26 [4.80] |
0.53 |
−3.88 [1.99] |
| 1977 | −51.83 [3.26] |
−49.37 [2.38] |
−27.99 [4.72] |
6.00 [1.32] |
0.62 [0.86] |
6.12 [6.16] |
19.49 [5.75] |
8.43 [4.50] |
0.51 |
−4.83 [2.56] |
| 1979 | −53.54 [2.94] |
−49.63 [2.24] |
−28.05 [4.30] |
4.89 [1.04] |
0.88 [1.16] |
6.21 [5.77] |
18.72 [6.47] |
8.59 [4.47] |
0.49 |
−5.23 [2.59] |
| 1981 | −56.81 [3.36] |
−44.78 [2.13] |
−26.20 [4.16] |
5.28 [1.09] | 0.70 [0.99] |
5.83 [6.08] |
18.84 [5.35] |
9.06 [4.59] |
0.47 |
−7.18 [3.54] |
| 1983 | −69.49 [3.77] |
−37.53 [1.79] | −25.21 [3.99] |
2.41 [0.55] |
1.02 [1.39] |
5.49 [5.22] |
19.08 [6.82] |
9.64 [5.11] |
0.50 |
−6.61 [2.89] |
| 1985 | −72.24 [5.06] |
−28.38 [1.48] |
−22.96 [3.56] |
0.23 [0.04] |
1.27 [1.74] |
5.13 [5.12] |
20.10 [6.64] |
10.29 [5.16] |
0.48 |
−6.96 [3.23] |
| TEST1 | 0.69 {0.00} |
TEST2 |
3.47 {1.00} |
The sample size for each regression = 231 |
||||||
1. Absolute White heteroskedastic robust t statistics for the null
hypothesis that βj equals zero are shown in square brackets [
]. |
||||||||||
The results again provide support for the propositions discussed in Section 3(a). In each period the coefficients on the capital/labour, skilled labour and land/labour ratios have the correct sign and the vast majority are significant at conventional significance levels. As in the case of the pooled regression results (presented in Table 6) the coefficient on the natural resource variable is the incorrect sign. It is, however, insignificant in most periods and plays little independent role in explaining variations in intra-industry trade across countries. This is particularly the case in the later years.
An examination of the 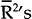 for the various years shows no significant
deterioration in the fit of the equation through time. This is in sharp contrast to the model
estimated by Helpman (1987). Using a similar specification to that used here, he proxied
resource dispersion by differences in per capita incomes. While his model fit reasonably well
for the first year of his sample (1970 – with an
for the various years shows no significant
deterioration in the fit of the equation through time. This is in sharp contrast to the model
estimated by Helpman (1987). Using a similar specification to that used here, he proxied
resource dispersion by differences in per capita incomes. While his model fit reasonably well
for the first year of his sample (1970 – with an 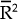 of 0.254) it
had collapsed by the final year (1981 – all coefficients were insignificant and the
of 0.254) it
had collapsed by the final year (1981 – all coefficients were insignificant and the 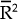 had fallen
to 0.039). This result led Helpman to conclude that the link between the share of intra-industry
trade and differences in factor composition had weakened through time. The results in Table 7,
however, suggest that this conclusion is not justified. Measuring relative resource endowments
more accurately, we find that the link between resource dispersion and intra-industry trade
remains strong.
had fallen
to 0.039). This result led Helpman to conclude that the link between the share of intra-industry
trade and differences in factor composition had weakened through time. The results in Table 7,
however, suggest that this conclusion is not justified. Measuring relative resource endowments
more accurately, we find that the link between resource dispersion and intra-industry trade
remains strong.
In Section 3 it was noted that the share of intra-industry trade in Japanese trade has been low and static. It has been suggested that this may be evidence of a protectionist trade and development policy. Numerous authors have also noted that for Japan the share of imports in GDP is relatively low. Estimating import penetration equations, Lawrence (1987) and Balassa and Noland (1988) find that Japan significantly under imports. They interpret this as evidence of protectionist trade policy. However, not all studies have reached this conclusion. Bergsten and Cline (1987) find that import penetration into Japan is not unusually low after controlling for a number of explanatory variables. Examining the share of intra-industry trade in total trade may be a better way of assessing the extent of protectionist policy. Protectionist policies aimed at restricting competition in certain key sectors may not reduce total imports but should reduce intra-industry trade.
To test whether the share of intra-industry trade in total trade for Japan can be explained by resource dispersion and country size the model is again estimated for each year with the inclusion of a dummy variable for Japan which takes a value of one if Japan is one of the trading partners and zero otherwise. The parameter estimates are essentially unchanged from those in Table 7 and are thus not reported. The last column of Table 7 does, however, report the coefficient on the Japan dummy variable. In each year, the dummy variable has a negative sign, but, up until the late 1970s the coefficient is insignificant. Since the late 1970s the dummy coefficient has increased in absolute size and become significantly different from zero.
These estimates suggest that in the 1960s, and at least the first half of the 1970s, Japan's low share of intra-industry trade could be accounted for by the fact that its resource base was substantially different from that of most of the other OECD nations. However, as its resource base has become more like many of the other OECD nations, the share of intra-industry trade has not increased. The structure of Japan's international trade remains highly specialized. This is consistent with the view that its development policies have been protectionist.
Footnotes
The results were essentially unchanged when the time trend was replaced by time dummies. [6]
Given the relatively poor results from the fixed effects estimator, the poor GLS results are hardly surprising. The GLS estimator can be interpreted as a weighted average of the fixed effects and between estimators. Given that the time series variation is much smaller than the cross sectional variation, the standard error of the regression is much smaller for the fixed effects estimator. Consequently, the fixed effects estimator receives a much larger weight in the construction of the GLS estimator than does the between estimator. [7]