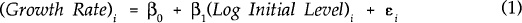RDP 9110: Resource Convergence and Intra-Industry Trade 2. Resource and Income Convergence

Philip Lowe

November 1991

We focus on five resources: labour, skilled labour, capital, agricultural land and natural resources. The endowments of each of the last four resources are divided by the labour force to obtain a measure of resources per worker. The labour supply is measured as the number of economically active people. Skilled labour is the number of workers who fall into International Standard Classification of Occupations (ISCO) classes 0,1 and 2. Such workers include “professional, technical and related workers” and “administrative and managerial workers”. The principal measure of the capital stock is calculated by cumulating investment over a fifteen year period assuming a depreciation rate of 5 per cent per annum.[4] The endowment of agricultural land is measured as the number of hectares of arable land and land under permanent crops. To obtain a measure of a country's natural resource endowment we use yearly production data for five raw materials: oil, coal, copper, iron ore, and zinc (see data appendix).

In order to formally test the convergence propositions we estimate the following equation for each relative resource endowment:

If convergence in relative factor endowments has occurred the growth rate should be negatively correlated with the initial level.[5] Given possible measurement error in the initial values both ordinary least squares (OLS) and instrumental variable (IV) estimates are presented for the capital/labour and skilled labour regressions. For each equation the instrument used is the log of initial per worker GDP. The estimation results are reported in Table 1. Results are not reported for the natural resource/labour ratio as they are dominated by very large changes in the resource ratio in just a couple of countries. An examination of the coefficient of variation for the natural resources/labour ratio does, however, show an upward trend through time.

Table 1: Regression Tests of Convergence in Resources
  PERIOD βOLS βIV 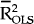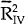Inline Equation Inline Equation N
1. CAPITAL/LABOUR RATIO 1965–85
 
 		 −0.99
(5.13)
[4.80]		 −1.00
(4.87)
[4.84]		 0.52
 
 		 0.52
 
 		 22
 
 
2. CAPITAL/LABOUR RATIO
(a) Manufacturing 1970–85
 
 		 −0.60
(2.37)
[2.94]		 −0.86
(1.36)
[1.59]		 0.32
 
 		 0.20
 
 		 14
 
 
(b) Agriculture 1970–85
 
 		 −1.46
(6.89)
[3.48]		 −1.25
(2.85)
[2.85]		 0.78
 
 		 0.76
 
 		 14
 
 
(c) Mining 1970–85
 
 		 −0.29
(0.45)
[0.81]		 −0.40
(0.45)
[0.60]		 −0.08
 
 		 −0.09
 
 		 11
 
 
3. SKILLED LABOUR RATIO 1965–85
 
 		 −0.48
(4.27)
[3.97]		 −0.49
(3.90)
[3.48]		 0.45
 
 		 0.45
 
 		 22
 
 
4. LAND/LABOUR RATIO 1965–85
 
 		 −0.06
(3.36)
[3.37]		   0.34
 
 		   22
 
 
NOTES
1. The dependent variable is the growth rate and the explanatory variable is the log of the level in the first year of the period. A constant (not reported) was also included in the estimated equation.
2. The instrument used is the log of the initial value of GDP per worker.
3. Absolute t statistics for the null hypothesis that β equals zero are shown in parentheses ( ). White heteroskedastic robust t statistics are shown in square brackets [ ].
4. Sectoral capital/labour data are only available for a subset of the OECD nations. For the manufacturing and agricultural sectors data for the following countries are used: U.S.A., Canada, Japan, Germany, France, Italy, United Kingdom, The Netherlands, Belgium, Denmark, Norway, Sweden, Finland and Australia. The same list of countries with the exceptions of Germany, France and Belgium are used for the mining sector.

Two sets of results are reported for the capital/labour ratio. The first uses the capital stock measure obtained from cumulating investment. The second uses direct measures of the capital stock for several sectors as calculated by the OECD. This second measure of the capital stock is, however, only available over the period 1970–1985 and for a subset of fourteen nations.

Using the full set of countries the coefficient on the initial level of the capital stock is negative and significant for both the OLS and the IV estimates. The results for the sectoral capital/labour ratios are mixed. There is strong evidence of convergence of the capital/labour ratios in the agricultural sector over the period 1970 to 1985. The results for the manufacturing sector are less strong but still suggestive of convergence. In contrast, there is little evidence of any tendency for countries with low initial capital/labour ratios in the mining sector to experience faster rates of capital accumulation in that sector. These results must be interpreted with a deal of caution due to the small number of available observations. The results for the skilled labour ratio support the hypothesis that relative skilled labour endowments of the OECD nations have converged over the period 1965 to 1985. The results for the land/labour ratio also suggest some convergence but at a very slow rate.

Dowrick and Nguyen (1989) argue that “income convergence where it has occurred does not appear to be the result of variations across countries in the growth of factor inputs; rather it results from a systematic tendency for catching up in total factor productivity”. While not disputing some role for the convergence in total factor productivity (TFP), the above results contradict Dowrick and Nguyen's assertion regarding factor inputs. Indeed, it appears that the convergence of capital/labour ratios and skilled labour ratios are an important part of the per worker income convergence phenomenon. To examine this issue in further detail we conduct regressions similar to those of Dowrick and Nguyen. Using a shorter time period we are better able to control for both physical and human capital accumulation.

The results reported in columns (1) and (2) in Table 2 are similar to those reported by Dowrick and Nguyen. Column (1) confirms the convergence in GDP per worker. Column (2) presents the results when the average investment ratio is used to proxy the growth rate in the capital stock. As Dowrick and Nguyen find this ratio has a positive coefficient. More importantly, the coefficient on the initial level of income remains highly significant and negative. This is, however, not the case when the growth rate in the capital/labour ratio (column 3) is used to measure the accumulation of capital per worker. The coefficient on the initial level of income per worker falls substantially and has a heteroskedastic robust t statistic of 1.94, while the coefficient on the growth in the capital/labour ratio is highly significant and positive. Further, when the growth rate in the skilled labour ratio is also included the coefficient on the initial level of income becomes essentially zero, while the two resource variables have positive signs and are significant.

Table 2: Analysis of Convergence of Growth Rates (1965–85)
  1 2 3 4
Log Initial GDP
Per Worker		 −0.59
(5.19)
[4.63]		 −0.58
(5.62)
[6.53]		 −0.13
(1.47)
[1.94]		 −0.01
(0.09)
[0.07]
Average
Investment/
GDP Ratio		   0.02
(2.36)
[1.61]		    
Growth Rate of
Capital/Labour
Ratio		     0.36
(7.31)
[14.78]		 0.39
(8.00)
[15.83]
Growth Rate of
Skilled Labour
Ratio		       0.19
(1.89)
[2.21]
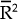Inline Equation 0.55 0.64 0.88 0.89

NOTES
1. Dependent variable is the growth rate in GDP per worker over the period 1965 to 1985.
2. A constant (not reported) was also included in the estimated equations.
3. Absolute t statistics for the null hypothesis that βj equals zero are shown in parentheses ( ). White heteroskedastic robust t statistics are shown in square brackets [ ].

The results suggest that the convergence of the capital/labour and skilled labour ratios have played a critical role in the convergence of incomes per worker in the OECD. We now turn to an examination of the theoretical and empirical implications of this resource convergence for the structure of international trade.

Footnotes

The capital stock was also calculated using a depreciation rate of 13 per cent per annum. No significant differences in the results using the two measures were found. [4]

Quah (1990) argues that even if the variance has remained unchanged through time such a regression will yield a negative coefficient on the initial level due to the “regression to the mean phenomenon”. The coefficients of variation for the capital-labour ratio, skilled labour ratio and income per worker each show a downward trend over the period supporting the hypothesis that there has indeed been some convergence. [5]