RDP 9111: Monthly Movements in the Australian Dollar and Real Short-Term Interest Differentials: An Application of the Kalman Filter 5. Estimation Results
November 1991
- Download the Paper 488KB
Summary statistics for all the data are presented in Table 1 (refer to Appendix 1 for a further discussion of data methods and sources). The first two rows display the sample means and standard deviations of real exchange rate changes over the post-float period. The sample means are positive, corresponding to real Australian dollar depreciation, for all countries except the United States and the trade-weighted index. The standard deviations for the United States and in the case of the trade-weighted index are around 45 per cent per month at an annualized rate, while other countries' exceed 50 per cent.
The next two rows of the table detail the same statistics for ex post real interest differentials. Sample means are negative across the board, indicating that real interest rates were higher on average in Australia than overseas. Sample standard deviations range from 3.5 per cent to around 6.5 per cent, highlighting the much greater volatility of real exchange rates compared with ex post real interest differentials over the post-float period.
The rational expectations framework implies that the ex post real interest differential comprises its ex ante equivalent and an unforecastable error. The variance of the ex post differential therefore forms the upper bound on the variance of the ex ante. Hence, an interpretation of the data consistent with rational expectations implies that the ex ante real interest differential in Australia over the post-float period has a low variance. A comparison with the variance of the real exchange rate could lead us to believe that real ex ante interest differentials are not variable enough to be capable of explaining the high variance of the real exchange rate. The econometric results of our paper provide more rigorous evidence of this.
The first six autocorrelations of the ex post real interest differential, calculated with the assumption of a zero true mean for the real interest differential, are reported at the bottom of Table 1. Alternatively, assuming the sample mean differential to be the true mean, similar but smaller autocorrelation values are obtained. Data for the United States, Germany and the trade weighted index reveal the largest autocorrelations, and suggest the possibility that the ex post real interest differentials follow some ARMA(p,q) process. Remaining countries' autocorrelations are smaller, beginning at 0.24 for the United Kingdom and 0.35 for Japan, and exhibit a much more irregular evolution.
Tables 2 to 5 provide estimation results for each of the bilateral currencies and for the trade-weighted index. Results are given for the two versions of the model. All coefficients, (β, ρ and λ are reported with asymptotic standard errors, together with the standard deviations of the error terms, σ1, σ2 and σ3 and the correlation σ13/σ1σ3. Variance decompositions reveal some of the implications of these estimates.
| Trade-Weighted Index |
United States |
West Germany |
United Kingdom |
Japan |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Log Likelihood: | 494.54 | 500.29 | 488.82 | 442.87 | 427.53 | |||||
| Parameters | s.e. | s.e. | s.e. | s.e. | s.e. | |||||
| β | 1.86 | (1.50) | 0.88 | (1.55) | 0.85 | (1.26) | 1.57 | (5.27) | 0.33 | (2.63) |
| ρ | 0.59 | (0.15) | 0.85 | (0.11) | 0.76 | (0.13) | 0.33 | (0.69) | 0.19 | (0.34) |
| λ | 0.88 | (0.33) | 0.43 | (0.48) | 6.87 | (—) | −0.54 | (17.78) | 5.41 | (—) |
| σ1 | 2.51 | 2.63 | 3.36 | 5.72 | 0.38 | |||||
| σ2 | 3.00 | 2.28 | 0.01 | 2.14 | 1.36 | |||||
| σ3 | 44.53 | 45.93 | 56.25 | 54.88 | 56.83 | |||||
| σ13/σ1σ3 | −0.30 | −0.20 | −0.12 | −0.30 | −1.00 | |||||
| Trade-Weighted Index |
United States |
West Germany |
United Kingdom |
Japan |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Log Likelihood: | 494.37 | 500.29 | 490.19 | 442.76 | 427.50 | |||||
| Parameters | s.e. | s.e. | s.e. | s.e. | s.e. | |||||
| β | 1.00 | (fixed) | 1.00 | (fixed) | 1.00 | (fixed) | 1.00 | (fixed) | 1.00 | (fixed) |
| ρ | 0.62 | (0.15) | 0.84 | (0.11) | 0.84 | (0.11) | 0.37 | (—) | 0.11 | (0.33) |
| λ | 0.79 | (0.21) | 0.46 | (0.44) | 0.52 | (0.37) | −2.31 | (—) | 0.76 | (1.95) |
| σ1 | 1.61 | 2.65 | 2.24 | 4.87 | 4.93 | |||||
| σ2 | 3.60 | 2.27 | 2.41 | 1.46 | 4.57 | |||||
| σ3 | 44.06 | 46.17 | 54.35 | 53.90 | 56.93 | |||||
| σ13/σ1σ3 | −0.08 | −0.23 | −0.09 | −0.27 | −0.13 | |||||
| Country | Variance Decompositions (%) | ||||||
|---|---|---|---|---|---|---|---|
| dt | qt | ||||||
| Et(dt,t+1) | et | Et(dt,t+1) | wt | Covariance | |||
| TWI | 69.54 | 30.46 | 14.28 | 101.64 | −15.92 | ||
| United States | 84.39 | 15.61 | 12.67 | 100.75 | −13.42 | ||
| West Germany | 100.00 | 0.00 | 4.49 | 100.73 | −5.21 | ||
| United Kingdom | 89.33 | 10.67 | 6.93 | 109.46 | −16.39 | ||
| Japan | 96.82 | 3.18 | 0.27 | 100.27 | −0.54 | ||
| Country | Variance Decompositions (%) | ||||||
|---|---|---|---|---|---|---|---|
| dt | qt | ||||||
| Et(dt,t+1) | et | Et(dt,t+1) | wt | Covariance | |||
| TWI | 57.32 | 42.68 | 3.79 | 97.80 | −1.59 | ||
| United States | 84.29 | 15.71 | 15.07 | 101.85 | −16.92 | ||
| West Germany | 79.77 | 20.23 | 8.74 | 95.66 | −4.40 | ||
| United Kingdom | 95.04 | 4.96 | 3.21 | 104.96 | −8.17 | ||
| Japan | 63.80 | 36.20 | 1.45 | 101.18 | −2.63 | ||
Parameter estimates are detailed in Tables 2 and 3 (following). For each model, log likelihood ratio tests fail to reject the hypothesis that β = 1 at a 95 per cent significance level. With β = 1, the risk premium is equal to zero. The low power of these tests, however, means that the restricted models (detailed in Table 3) could not be rejected with β equivalent to values less than 1. Remaining coefficient, variance and covariance estimates are robust across alternative restrictions over β.
Therefore, the value ascribed the time-varying risk premium in this model does not affect any of the conclusions. This result is disappointing since without conclusive evidence to either accept or reject the existence of a risk premium, it is not clear whether Campbell and Clarida's (1987) model collapses to a simple UIP specification for which little empirical support can be found.
Remaining parameter estimates are interpreted below. For explanatory convenience, we concentrate on the results obtained from the uncovered interest parity model of Australia's real exchange rate with a constructed trade-weighted index[35] (refer Table 3):
- ρ is estimated at 0.62, revealing moderate persistence in the ex ante real short-term interest differential between Australia and this trade-weighted index.
- λ is estimated at 0.79, suggesting that innovations to the AR(1) process involve errors associated with forecasting inflation in period t−1.
From the parameter estimates, we can calculate the coefficient on the ex ante real interest differential in equation [10] described in section 3. For the trade weighted index case, this coefficient assumes a value of 2.6 in the uncovered interest parity model and 4.5 in the linear risk premium model.[36] This implies, for the former model, that a 1 percentage point increase in the annual ex ante real interest differential, ceteris paribus, will induce a 0.2 percent change in the real exchange rate.
Estimates of the variances σ1, σ2, σ3 and the covariance σ13 are used for variance decompositions reported in Tables 4 and 5.[37]
For the trade-weighted index case, the proportion of the variance of the real exchange rate (qt) accounted for by the innovation variance of the ex ante real interest differential (vt) is approximately 3.79 per cent for the uncovered interest parity model and around 14.28 per cent for the linear risk premium model. Robust across all models and countries, the innovation variance of the expected long-run real exchange rate must explain the greatest proportion of the variance of the actual real exchange rate because ex ante real interest differentials do not.
It is important to note that when the proportion of the variance of the real exchange rate accounted for by the innovation variance of the expected long-run real exchange rate (u3t) exceeds 100 per cent, this does not imply zero explanatory power for the ex ante real interest differential. The existence of covariance between the two explanatory variables makes direct interpretation of the variance decompositions difficult. However, the overwhelming result remains clear: the movement in the real Australian dollar exchange rate over the period of this study is predominantly explained by the innovation variance of the long-run real exchange rate.
Ex ante real interest differentials are incapable of explaining the variability of the Australian dollar real exchange rate because the models' estimates of their persistence (that is, the ρ values), although quite high in some cases (estimates for ρ exceed 0.6 in half of the models estimated) are nevertheless insufficient to compensate their minor standard deviation[38] relative to that of changes in the real exchange rate.[39]
In summary, the results implied by direct application of Campbell and Clarida's (1987) methodology to Australian data do not contradict the idea that over a short horizon, a change in the level of Australia's real interest rates relative to the rest of the world ceteris paribus, exerts some small influence on the real exchange rate. They do indicate, however, that given the influence of all remaining factors, this effect is not substantial enough to be responsible for the monthly variability observed in the real exchange rate.
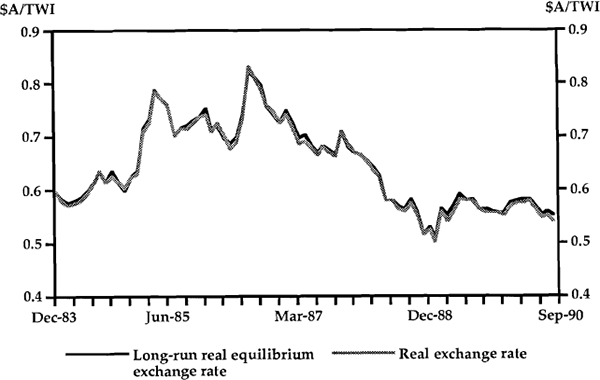
This conclusion can be illustrated graphically:
Graph 1 plots the real exchange rate against its observable long-run real equilibrium rate (wt
as estimated by our model) for Australia and a constructed trade-weighted index. They track so
closely that the reader may be forgiven for not seeing two different sets of data. This
demonstrates that the 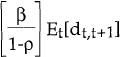 term in equation [10] is so small as to be
insignificant.
term in equation [10] is so small as to be
insignificant.
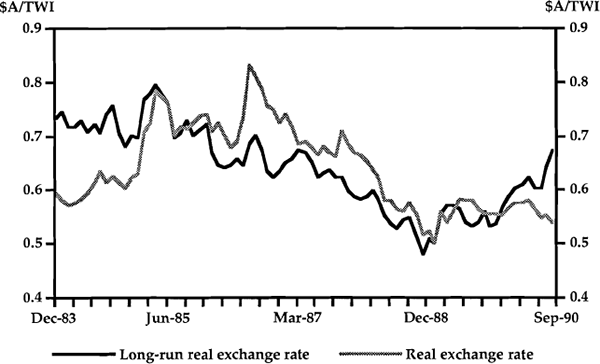
Graph 2 is offered as a counterpoint. It illustrates what the expected long-run real exchange rate would have looked like if the ex ante real interest differential between Australia and the trade-weighted index had been almost perfectly persistent. That is, we synthesize a series for the ex post real interest differential such that the model then estimates a value for ρ (the coefficient on the AR(1) process characterising the ex ante real interest differential) very close to 1. This significantly reduces the explanatory power of the expected long-run real exchange rate and verifies that wt in Graph 1 is not just an artifact of the model. The lack of explanatory power found in short-term real interest differentials is not a function of the model's assumption that the expected long-run real exchange rate (like the actual real exchange rate) follows a random walk.[40]
Footnotes
United States 42.65%; Japan 35.63%; and West Germany 21.74%. [35]
The spread of these coefficient values is a reflection of the lack of certainty associated with point estimates. [36]
Structural interpretation of the variance decompositions is not unambiguous; they do not imply unidirectional causality. [37]
The standard deviation of ex post real interest differentials, calculated in Table 1, is very small in comparison to that calculated for the mean change in the real exchange rate. Our rational expectations framework implies that the variance of the ex post differential forms the upper bound on the variance of the ex ante differential. [38]
Campbell and Clarida (1987) find that for the US, higher estimates of ρ are largely
accompanied by a smaller share of the ex ante differential in the variance of
the ex post differential. This is not always the case in the Australian
data.
Also in contrast with the findings of Campbell and Clarida (19871, we find
that ex ante real interest differentials, as opposed to inflation innovations,
account for the greater proportion of the variance of ex post
differentials. This is not surprising, since inflation exhibits very little variability
over a short time horizon.
[39]
It should also be noted that our sample period encompasses a regime shift in 1987. Between early 1985 and late 1987, monetary policy was directed towards both internal and external objectives. Short-term interest rates were used to directly target the exchange rate and the market expected central bank intervention to dampen any speculative activity. Post-1987, monetary policy became directed primarily towards an internal objective (Macfarlane and Tease (1989)). While it is possible that expectations for Australian dollar movements relative to interest rate changes may be different across these two periods, our results are not unique in the literature. We suspect that estimation of the model over a shorter sample period would produce negligible changes. [40]