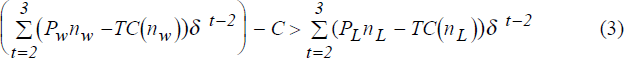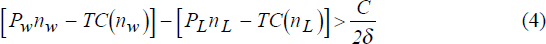RDP 9310: Explaining the Recent Performance of Australia's Manufactured Exports Appendix A: Model Assumptions
August 1993
- Download the Paper 109KB
A three-period model is used to illustrate the effect of a shock that is subsequently reversed. The initial period is one in which there are no exports because of the presence of sunk costs. In the second period, a shock occurs that makes exports profitable; firms make the decision to export sequentially (one by one), changing the number of firms that export and, thereby, the market structure. In the final period, the shock is reversed but the changed market structure ensures that output continues to be sold overseas. In each period, a representative firm must decide how much to produce[47] and whether it should export. Exporting output involves paying a sunk cost, C. There is an order of magnitude more firms in the world market than in the domestic market. Switching output between the two markets therefore changes PL but not PW. For simplicity, it is assumed that an individual firm ignores its own effect on PL when it maximizes profits. However, the next firm in the sequential decision making process makes its decisions using the altered PL.
In the standard model, the gap between supply and demand at PW is exported. However, in the presence of a sunk cost, if a firm is to export it must make extra profits (compared to selling domestically), the discounted sum of which is at least enough to cover the sunk costs. For the sake of simplicity, it is assumed that exports will occur as soon as this is the case. (This is contrary to Dixit (1989) where it is shown how it can be optimal to wait.)
In the presence of C it will be optimal for a risk-neutral firm to export all its output, if it exports any.[48] Hereafter, an ‘exporting firm’ is one that exports all its output. For a given number of exporting firms, local and total supply may then be defined.[49]
It is assumed that a firm will export as soon as the sum of the present value of profits from exporting exceeds the sum of the present value of profits from selling locally. This requires that firms ignore the variance of prices. Given an assumption that all shocks are thought to be permanent, entry will occur in, say, the second period if:
where
| nL | output sold locally by a representative firm |
| nW | output exported by a representative firm |
| TC(nL+nW) | total cost function |
| δ | 1 – the discount rate |
If δ is close to unity, this yields an expositionally useful approximation:
Ignoring discounting (δ = 1), this approximation states that the decision to export will be made if, in each of the two remaining periods, at least one-half of the sunk cost can be recouped. The presence of discounting merely says that a firm needs to expect to do a little better than this before it will export, to cover the opportunity cost of spending C.
If the TC function were known, it would be possible to solve the above inequality for PW−PL (d hereafter), at least numerically.[50] The ‘export premium’, d, is clearly an increasing function of C.[51] The top of the band of inaction is d. That is, PW must exceed PL by at least d before it will be profitable to export. The bottom of the band of inaction is zero because a local price above PW will immediately result in a representative firm ceasing to export.
The diagrams in the text are consistent with this simple model.
Footnotes
It is assumed that there is no production smoothing and that firms maximise profits over the whole three periods. [47]
Given PW is higher than PL, once the sunk cost is paid it makes sense to sell all the output at the higher price. A proof is available from the authors. [48]
Total supply (S) is the output of all firms for each price level. It is obtained by the horizontal summation of all firms' marginal cost curves. Local supply (s) is the sum of the marginal cost curves for the firms that sell all their output domestically. [49]
Experimentation with simple TC functional forms often produced analytically intractable results because nL is functionally related to PL. [50]
Furthermore, in this three period model d will actually change size each period because there are fewer periods in which to cover the sunk cost. This is ignored as it does not change the sense of the results. [51]