RDP 9310: Explaining the Recent Performance of Australia's Manufactured Exports 3. A Sunk Cost Model

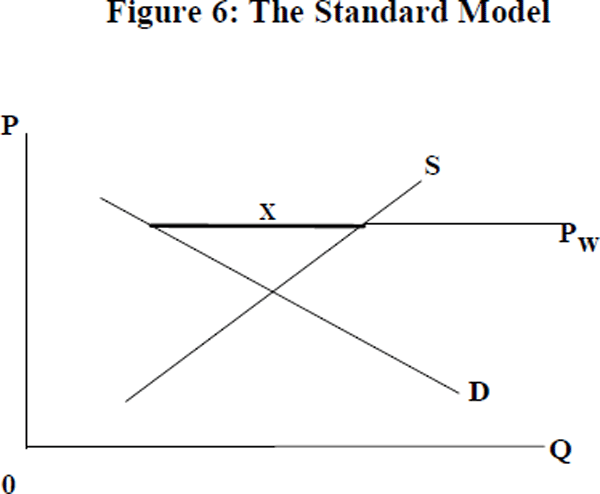
Consider first the properties of the standard export model. In this model, domestic firms compete in perfectly competitive markets. Entry into the world market is assumed to be costless and there are no transportation costs. Firms are price takers in the world market for traded goods and hence, the local price (P_L) and the world price (P_W) are the same when expressed in a common currency. The quantity of goods exported equals the excess of domestic supply over domestic demand, as shown in Figure 6.

What will be referred to as the ‘sunk cost model’ is the standard model with an additional assumption; firms must pay a once-off sunk cost (C) when they first export. Exporting will only commence if it improves the expected present value of profits by at least C. In general, the presence of C drives a wedge between the local price and the world price. There is no automatic tendency for P_L to equal P_W, because there is no profitable way for firms to exploit the difference in prices.

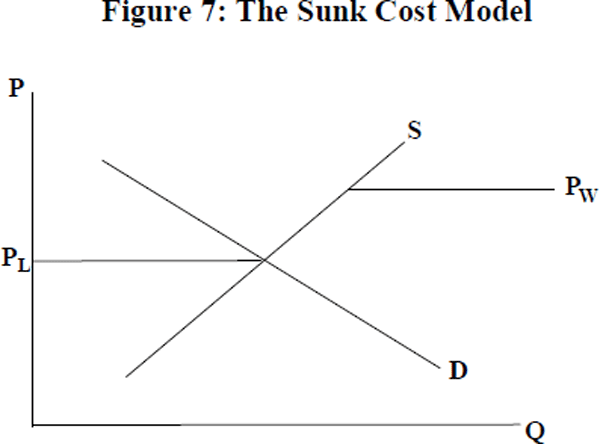
In general, models that incorporate sunk costs are characterised by a ‘band of inaction’ where movements of a causal variable within some band fail to have an effect. For example, an exchange rate band of inaction in an export model refers to a range of values for the exchange rate (the causal variable) that will not motivate firms to commence or cease exporting. The so called ‘lower bound’ of the band of inaction is the value of the exchange rate that will make local firms export for the first time, while the ‘upper bound’ is the value of the exchange rate that will make hitherto exporting firms cease exporting.^[8]

In the sunk cost model of this paper, the causal variable is the price differential P_W−P_L. A high value of the differential (the upper bound) will motivate firms to commence exporting, while a low value (the lower bound) will motivate exporting firms to cease exporting and instead sell their output on the domestic market. Movements of the price differential within the band of inaction (i.e. between the upper and lower bounds) will not change the number of exporting firms. For simplicity, the upper bound will be referred to as d, while the lower bound will be assumed to be zero.^[9] Subsequently, a change in the number of firms involved in exporting will be referred to as a ‘change in market structure’.

Dixit (1989) discusses the factors that influence the width of a band of inaction. In his model, the degree of variation in the causal variable is shown to be a surprisingly important determinant of the width of the band; the greater the variation the wider the band. Using numerical examples, he also argues that variability in a causal variable can create a wide band of inaction even if the sunk costs are quite small.^[10] This insight becomes important when evidence is presented for the existence of sunk costs.

To see how variability can influence the band of inaction, imagine that P_W−P_L is a random walk. For expository ease, assume that a firm faces this choice in each period: it can pay the sunk cost and then export forever or it can sell domestically and put off till the next period the decision about when to enter the export market. Further assume that, for the first time, P_W−P_L has risen to a level high enough for potential exporters to just cover the sunk cost C. That is, the expected present value of exporting now is zero.^[11] The current price differential would be the top of the band of inaction (i.e. exports would commence) if the future value of P_W−P_L was not expected to vary. However, in the presence of future variability it is not optimal to export immediately. Since it is possible that P_W−P_L will rise further, a rational firm can do even better by remaining uncommitted for one period. If the price differential does rise, the firm can pay the sunk cost then and get a positive expected present value. If P_W−P_L falls next period, it can decide not to pay the sunk cost, and wait a further period. Viewed from the original period, the expected present value of waiting is positive, while the expected present value of exporting immediately is zero.

Nevertheless, this does not imply that there is no upper bound. If P_W−P_L in the current period is high enough for exporters to cover sunk costs and earn a return in the current period, there is an opportunity cost of waiting. There is, therefore, a value of P_W−P_L which is so high that the foregone revenue associated with waiting equals the benefit of waiting. A value of P_W−P_L higher than this motivates exports immediately. This is the true upper bound (d). The band of inaction is, therefore, wider because of the variation in the causal variable.^[12]

Earlier literature has tended to focus on the exchange rate as the sole source of movements in P_W−P_L. However, changes in world demand or domestic demand will also alter this price differential. Therefore shocks to exports via these causal variables will now be examined.^[13] The hysteretic effect on exports of a subsequently reversed shock will be shown diagrammatically. The shocks considered will be classified as external (changes in world demand or the exchange rate) and internal (changes in domestic demand). Some other market-altering shocks will also be considered.

A simple three-period model consistent with the following diagrammatic exposition is described in Appendix A. Firms sell all their output overseas or domestically; they do not sell some in each market. Shifts in market structure are equivalent to shifts in a local supply curve. This curve is the horizontal summation of the marginal cost curves of those firms supplying the local market at a point in time.

Firms make their export decisions sequentially according to the following rules:

View MathML

In addition, local and exporting firms choose output so that marginal cost is equated to the relevant output price: P_L and P_W respectively.

3.1 External Shocks: The Exchange Rate and World Demand

Exchange rate depreciation or an increase in world demand should, other things being constant, be reflected in a rise in the world price of exports, when measured in local currency.^[14] The hysteretic effects of such an external shock, and its subsequent reversal, are now shown. Figure 8 shows the situation in period one, before the shock.^[15]

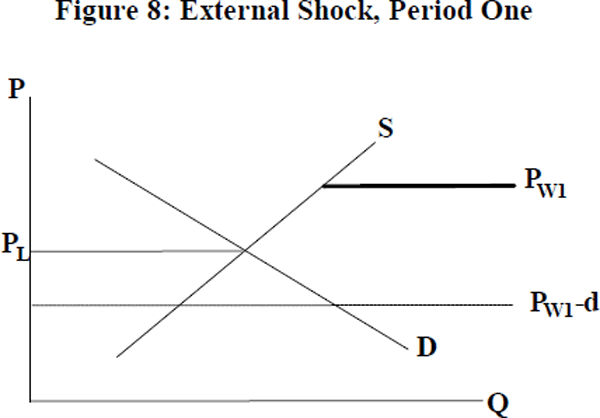
Local supply and demand are equated at P_L, and P_W−P_L is in the band of inaction. There are no exports: the higher price for exports will not compensate a firm adequately over the three periods for its entry cost. In Figure 9, the world price rises due to an external shock.

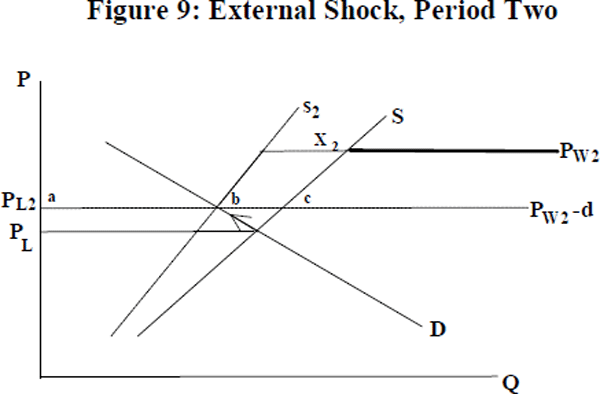
The new world price exceeds P_L (the local equilibrium) by more than d; firms will want to export. As firms leave the domestic market one-by-one, domestic supply^[16] contracts toward s₂, putting upward pressure on the local price. This process continues until the marginal firm no longer faces a local price that differs from the world price by more than d. The new equilibrium has a proportion, bc/ac, of exporting firms. However, the level of exports is not bc. As exporting firms are producing up to the point where marginal cost equals world price, the level of exports is shown by the segment x₂ between the two supply curves at that price. Now consider the reversal of the shock so that P_W returns to its initial level (see Figure 10).

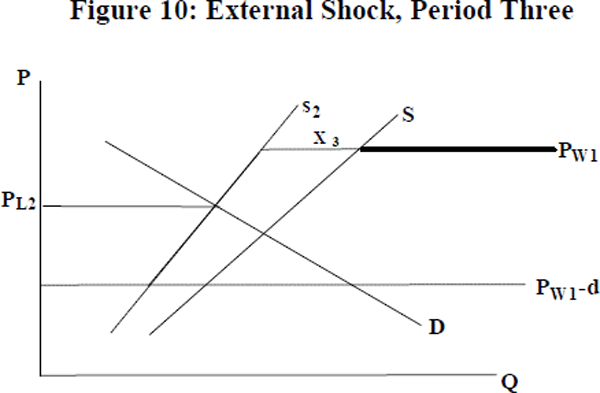
As P_W falls, the differential between P_W and the new P_L falls into the band of inaction. It will not be optimal for any new firms to export. As P_W falls each exporting firm will produce less output. Aggregate exports will fall to x₃ as a result. However, firms that have already paid their sunk costs will continue to export, so long as the world price is higher than the local one.^[17] Thus, despite a reversal of the shock, some exports continue to occur. There is hysteresis.

3.2 Internal Shocks: Domestic Demand

In this section the hysteretic effects of a large decline in domestic demand, and its subsequent reversals, are shown. Figure 11 shows the situation in period one, before the shock. Again, no firm is initially exporting.

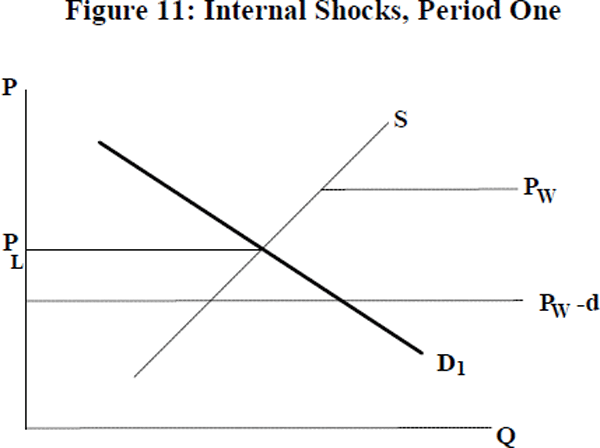
In the second period there is a fall in domestic demand so that D₁ shifts to D₂.^[18]

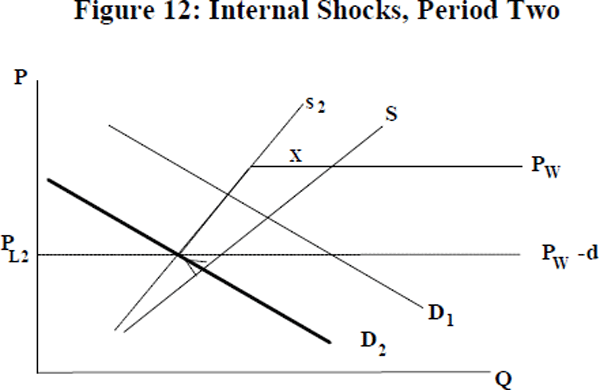
The decline in demand initially results in a local price which differs from the world price by more than d. Local supply will therefore fall to s₂ and exporting will occur. When the shock is reversed (and demand shifts back to D₁) what will happen to exports?

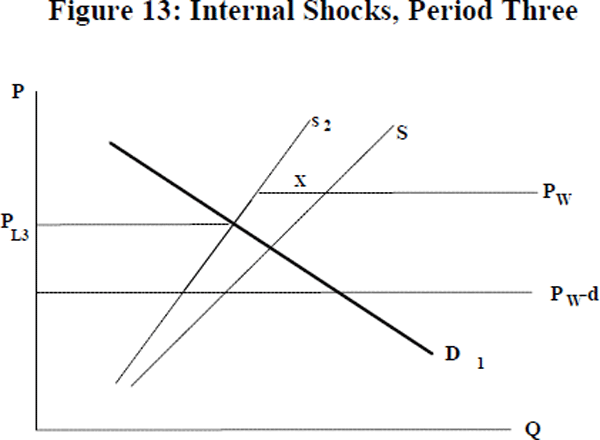
As local supply has contracted, the new local price will be higher than it was in period one. The price differs from P_W by less than d, stopping entry of new firms into the export market. However, firms that have paid their entry costs will continue to export. There is no change in aggregate exports because the output price for these exporting firms has not changed. This is in spite of the shock being reversed. There is hysteresis.

The differences between the sunk cost model and the standard model are most apparent in the face of an internal shock. Unlike the standard model, shocks to domestic demand which leave P_W−P_L in the band of inaction have no effect on aggregate exports. However, external shocks alter output for every exporting firm by changing P_W (the output price). Provided that some firms are exporting, any external shock will affect the aggregate (as in the standard model), even if there is no change in market structure.

3.3 The Vanguard Effect

It has been shown that firms that have already paid their sunk costs will continue to export, so long as the world price is higher than the local one. In the popular vernacular, each firm has established a ‘beachhead’ so that export sales are not given up when market conditions change. In fact, ‘beachhead’ is often used as a metaphor for hysteresis in exports. However, the beachhead notion may be applied to a group of firms, as well as an individual firm. A military beachhead enables later forces to enter the battle more easily. With regard to exports, initial entrants may form a ‘vanguard’ which reduces the sunk cost for subsequent entrants.^[19]

In terms of the model, a fall in C makes it optimal for firms to leave the local market in response to a smaller price differential. Consider the extreme case where one firm paying C means that other firms do not have to pay C. The final period solution of the model for all three shocks is shown in the following diagram.

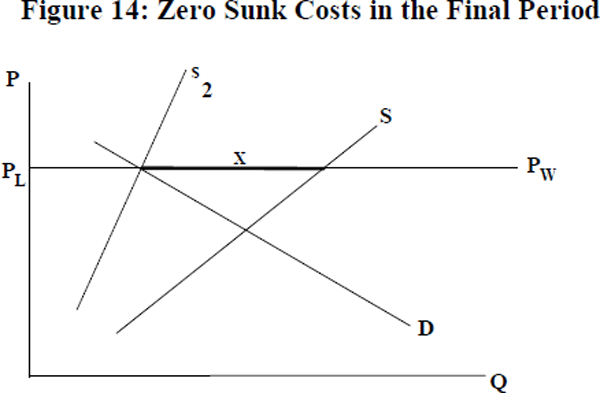
This can be recognised as the standard model. A comparison with the final equilibria for both the internal and external shocks shows that hysteresis can be magnified by the effects of a vanguard.^[20]

3.4 Tariff Reductions

The discussion thus far has been restricted to movements in world price, domestic demand and sunk costs. This restriction has facilitated the discussion of hysteresis using the sunk cost model. However, an important class of shocks can be represented by a shift in the supply curve.^[21] If declines in protection result in cheaper imported inputs, the cost curves for Australian manufacturing will shift down. This is equivalent to an outward shift in the supply curve. In the following diagram, imported inputs are an argument of supply.

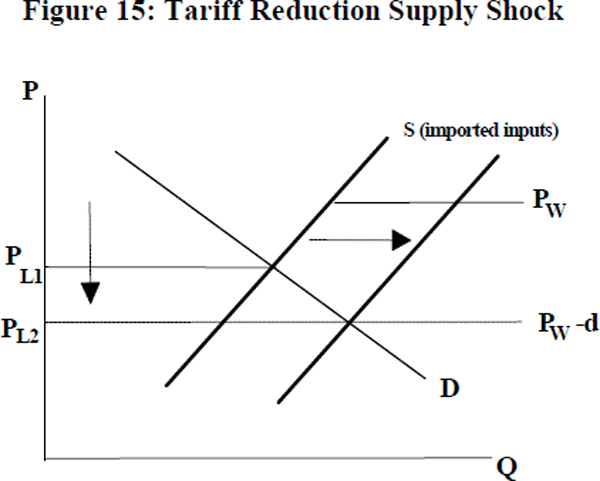
While P_W−P_L remains in the band of inaction, no new firms will export. However, exports will increase if P_W−P_L exceeds d. Therefore efficiency gains from cheaper imported inputs (or microeconomic reform) could induce an apparently ‘sudden’ rise in exports.

It has been established that the presence of sunk costs brings with it the possibility of hysteresis. The source of hysteresis may be world demand or domestic demand, in addition to the more conventional exchange rate channel highlighted in earlier models. Furthermore, the sunk cost model describes two facets of international integration. Export vanguards reduce sunk costs for subsequent entrants, thereby accelerating the momentum of an export surge. Tariff reductions (or microeconomic reform) may proceed for some considerable time, apparently without effect. In reality, the outward shift in the supply curve places downward pressure on local prices without effecting exports, until a threshold is reached where new exporters can cover their sunk costs. The resultant growth in exports may appear to be sudden, and unrelated to its true explanators. In what remains of the paper, an attempt is made to relate the experience of the 1980s to the analytical framework that has been developed.

Footnotes

The exchange rate in this example is expressed as the foreign currency price of the local currency. [8]

In other words, when the local price exceeds the world price a representative firm will cease exporting and instead sell on the domestic market. This is consistent with the simple model in Appendix A, but not with the more sophisticated analysis of Dixit (1989) subsequently discussed in the text. [9]

However, sunk costs must be non-zero for there to be a band of inaction. [10]

Here and subsequently, the ‘present value of exporting’ refers to the value of the extra profits attainable compared to selling locally. [11]

Dixit (1989) also shows how the lower bound falls with increased uncertainty in the causal variable. [12]

The issue of how the future variances and covariances of the causal variables effect the width of the band of inaction is sidelined. A formal extension of Dixit (1989) which allows for these variances and covariances is not attempted. The model in Appendix A assumes that firms export as soon as sunk costs can be covered. [13]

This abstracts from productivity shocks which would effect both the exchange rate and the total supply curve. See Appendix C for a discussion of the associated empirical difficulties. [14]

In subsequent diagrams, numerical subscripts denote the time period. [15]

If the local price rises above P_w or falls below P_W−d, the number of firms supplying the domestic market changes. This is shown graphically by dashing the s line outside these limits. [16]

That is, while P_W−P_L exceeds the lower bound of the band of inaction. [17]

The local demand for the exportable good shifts in response to GNE. [18]

A vanguard is the ‘foremost part of an army or fleet’ (Oxford Dictionary). Its existence creates a free-rider problem. It also may help explain the existence of industry organisations the role of which is to facilitate entry of firms to foreign markets. If it is a policy objective to increase exports, the government can subsidize the vanguard. As well as encouraging outward focus, organisations such as AUSTRADE already fulfil this purpose. For example, Export Marketing Development Grants cover marketing expenditures of firms which export less than $25 million worth of merchandise. [19]

An interesting corollary to the vanguard effect is that future hysteretic effects will be less pronounced if the sunk costs are made smaller by the vanguard. [20]

Some of these shocks, such as microeconomic reform and tariff reductions, are not expected to be reversed and therefore cannot be ‘hysteretic’ in the strict sense of the word. They are, nevertheless, interesting. [21]