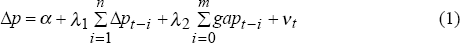RDP 9411: Demand Shocks, Inflation and the Business Cycle 2. Background
December 1994
- Download the Paper 72KB
Much of New Keynesian economics is built around the “stylised fact” that, given wages, changes in demand have no (or little) effect on prices.[2] As Blanchard and Fisher (1989) note, the simplest explanation is that given wages, marginal cost is flat so that firms have no reason to increase prices as demand increases. An alternative explanation is that marginal costs increase as output increases, but that markups are counter-cyclical so that prices remain unchanged.
There is considerable debate about both the theoretical and empirical justification for believing that markups narrow when demand and output are high. At the theoretical level, various arguments have been advanced to justify this relationship. First, there may be some price-smoothing, whereby the seller agrees not to change the price fully in line with production costs, especially when changes in costs are seen as temporary. Second, the elasticity of demand facing a firm may be pro-cyclical, so that market power is reduced when demand is high. Third, it may be more difficult for firms to collude when demand is strong, as the benefit from cheating is likely to increase as demand rises.[3]
On the other hand, “customer markets” models suggest that markups should increase as demand rises. In these models, a firm that lowers its price sells more to existing customers and expands its customer base. In so doing, it also increases future sales. Lower prices are thus an investment in market share. Such investments are likely to be more profitable, the higher is the ratio of future to current sales. As a result, discounting will be more common at low levels of demand and thus markups should decline when demand falls.[4] When demand is high (relative to potential) the cost of losing customers is reduced and margins should widen.
The empirical evidence on the relationship between markups and demand is mixed. There is no strong consensus about whether the markup is pro or counter-cyclical, or which theories of the markup are most empirically relevant. Rotemberg and Woodford (1991), Bils (1987), and Benabou (1992) find that the markup is counter-cyclical in the US. On the other hand, Ramey (1991) finds that US markups are pro-cyclical. Rae and Wong (1992) find a similar result for New Zealand, while Morrison (1988) finds that markups are pro-cyclical for manufacturing firms in the United States but counter-cyclical for manufacturing firms in Japan.
In a study concentrating on French and German manufacturing firms, Konig and Nerlove (1983) find that firms' actual and expected price changes were largely independent of actual and expected demand changes. This was particularly the case for French firms. Price changes were found to be driven largely by costs, with firms reacting to demand changes by altering production levels. Even in the presence of capacity constraints, this study found that firms are more likely to revise production, rather than prices, in response to an unexpected change in demand. Buckle and Meads (1991) find similar results in their investigation of the behaviour of manufacturing firms in New Zealand.
If it is correct that markups are counter-cyclical, then the power of the output gap in explaining prices rests on the link between the level of output and costs. This link is simply the familiar Phillips Curve relationship between unemployment (or the output gap) and wages growth.
An increase in the level of output may increase costs in one of two ways – marginal costs may increase because of decreasing returns (at least in the short run), or factor prices may rise, increasing production costs, even if firms are operating under constant returns to scale.
With some factors of production fixed in the short run, marginal cost may increase quite quickly (even with constant factor prices), especially once production exceeds normal capacity. Machines are worked at above normal capacity, increasing wear and tear, bottlenecks may occur in the production process, and new workers may be less skilled than the firm's existing workers. In addition, Bils (1987) argues that marginal costs rise with output, not solely because the capital stock is fixed in the short run, but also because high capacity utilisation requires the use of relatively expensive overtime. He finds that marginal costs increase with output. In contrast, Ramey (1991) and Flaig and Steiner (1989) find that marginal costs decline with output.
While this first link between capacity and costs holds at the level of individual firms, the second link (that is, increasing factor prices) depends upon a high level of capacity utilisation for the economy as a whole. In such cases, aggregate demand for factors of production (including labour, capital and raw materials) is relatively high. Just as is the case for final goods, strong demand puts upward pressure on input prices. This pressure can arise through increasing costs of producing inputs and through higher margins on various factors of production. Stronger demand for raw materials, for example, may require firms to exploit higher-cost sources, leading to higher marginal costs. In the labour market, stronger demand increases the market power of unions and this may be translated into increases in wages. If the markup in the labour market is defined as the difference between the actual wage and workers' reservation wage, there is little reason to believe that the markup is counter-cyclical – in fact, the reverse is probably true. Thus with pro-cyclical markups in factor markets and increasing marginal costs of producing inputs, strong demand should lead to higher factor and output prices, even if producers of final goods operate under constant returns to scale in the short run.
There is considerable empirical support for the idea that increased capacity utilisation increases price pressures in the economy. Bauer (1990) finds that in the United States, inflationary pressures increase when the Federal Reserve's capacity utilisation series rises above 80 per cent. These pressures appear to be stronger in goods markets than in markets for services and are attributed to increasing marginal costs as capacity constraints are reached. McElhattan (1985) finds similar results, but argues that the link between capacity utilisation and inflation arises from markups being pro-cyclical. She also finds that capacity utilisation is a better predictor of inflationary pressures than the unemployment rate (a measure of excess capacity in the labour market). In a comprehensive review of the effect of capacity constraints on output and prices in the US, Shapiro (1989) shows that prices do rise when capacity utilisation rises, but not more so than that suggested by the increase in wages. The implication is that marginal productivity is not decreasing with output and that markups are not pro-cyclical. Indeed, in some industries studied by Shapiro, prices rise less than costs at high levels of capacity utilisation.
In Australia, Blundell-Wignall, Lowe and Tarditi (1992) find that the inclusion of the output gap in an autoregressive model of inflation significantly improves the equation's explanatory power. They argue that excess capacity typically precedes troughs in inflation, while increasing inflation typically follows periods when output is above some notion of “potential” output. The most notable exception to this relationship appears to be in the late 1980s, when the Prices and Incomes Accord was moderating wage pressures that might normally have been expected when the level of output was high and increasing. By holding down wage increases, the Accord was able to reduce the rate at which firms' costs were increasing. This allowed inflation to actually decline slightly in a period of very strong demand growth and declining unemployment.
Finally, before turning to the survey data, we examine the relationship between the output gap in manufacturing and manufacturing price inflation using output and price data for the manufacturing sector. To do this, we estimate the following equation:
where Δp is the quarterly percentage change in the price of manufactured goods and gap is a measure of the output gap in the manufacturing sector. Lags of quarterly inflation are included to capture the fact that inflation rates are often characterised by a considerable degree of inertia. Changes in costs are excluded, as the output gap variable should capture cost pressures.
The output gap is the gap between the actual and potential levels of manufacturing output. We calculate potential output using the method developed by Hodrick and Prescott (1980) and also by using a time trend through the log of actual output. Both methods have the undesirable property that the measure of potential output for the last few observations in the sample can be excessively influenced by the current level of actual output. In an attempt to obtain a better measure of potential output, we assume that manufacturing output will grow at a quarterly rate of 2 percent over each of the next 5 quarters. Having made this assumption we estimate both measures of potential output using a sample period that runs from September 1968 to September 1995. Equation (1) is then estimated over the period September 1977 to June 1994.
We initially include the contemporaneous value and four lags of the output gap as explanatory variables, as well as four lags of quarterly manufacturing prices inflation. We sequentially eliminate insignificant lags. For both measures of the output gap this leaves us with a specification which includes two lags of quarterly inflation and the contemporaneous output gap. The estimated results are reported in Table 1.
| Hodrick-Prescott Output Gap | Trend-Adjusted Output Gap | |
|---|---|---|
| Constant | 0.54** (2.83) |
0.63** (3.13) |
| Inflation(t−1) | 0.40* (2.42) |
0.38* (2.31) |
| Inflation(t−2) | 0.25 (1.91) |
0.23 (1.80) |
| Output Gap | 5.71* (2.22) |
5.74* (2.30) |
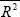 |
0.39 | 0.40 |
| Diagnostic Test: Serial Correlation |
1.88 {0.39} |
1.81 {0.41} |
| Notes: White corrected t-statistics are reported in parentheses. Numbers in brackets {} are p-values for a test of the null that regressions are first or second-order serially correlated. | ||
The results confirm an important role for the output gap in influencing price changes in the manufacturing sector. The contemporaneous output gap coefficient is positive and statistically different from zero. While the results suggest that high capacity utilisation will lead to immediate price pressures, there are also important delayed effects. A one percentage point decline in the output gap for the manufacturing sector, for just one quarter, results in an immediate decline in the quarterly rate of price inflation for manufactured goods of 0.06 of a percentage point. After one year, the price level will be 0.12 percent lower than otherwise would have been the case.
Footnotes
This stylised fact leads Blanchard and Fisher (1989) to ask “Why are shifts in demand largely accommodated by changes in quantities rather than by changes in relative prices?” (p. 427) or more specifically “why [do] shifts in the demand for goods lead mostly to movements in output rather than movements in prices given wages” (p. 427). [2]
For a review of various models of the mark-up see Rotemberg and Woodford (1991). [3]
See for example, Phelps and Winter (1970) and Greenwald and Stiglitz (1988). [4]