RDP 9411: Demand Shocks, Inflation and the Business Cycle 3. The Survey

The above aggregate data for the manufacturing sector provide a useful summary of the relationship between capacity utilisation (or the output gap) and changes in inflation, however, it leaves us without answers to two important questions. First, how are demand pressures transmitted into increased price pressures? Second, to what extent do firms react differently to unexpected and expected changes in demand? We turn to survey data in an attempt to shed some light on these two questions.

The survey data we use are from the ACCI/Westpac Survey of Industrial Trends. This survey is conducted quarterly and typically includes responses from around 200 manufacturing firms, drawn from a sample of over 400 firms each period. The sample is designed to reflect, as closely as possible, the size and industrial composition of the manufacturing sector.

Each firm is asked questions regarding its actual and expected new orders, prices, costs, output etc. These questions are qualitative and the majority are directed at the firm's experience over the previous three months and their plans, or expectations, for the next three months. Firms are asked to abstract from normal seasonal variations, and indicate whether a particular variable has increased, decreased or stayed the same over a given period. The percentage of firms reporting an “increase”, “decrease” or “no change” is published for each question. In the following analysis, we focus on the questions relating to new orders received (our demand variable), output, average selling prices and average cost of production. We also use the responses to the question which asks whether firms are operating at, above, or below normal capacity.^[5]

An advantage of using this type of survey data is that it allows direct observation of both expected and actual outcomes. This permits us to avoid some of the pitfalls involved in generating expectations using macroeconomic data. In particular, using the residuals from an econometric model of demand as a measure of unexpected demand changes and then correlating those changes with unexpected changes in inflation generated in a similar way, may lead to misleading results regarding the underlying correlation between the two shocks. This is problematic if some information which is actually used by firms in forming expectations is omitted from each equation. In this case, any correlation in the estimated shocks may simply reflect this omitted information.^[6] In addition, the survey data allow us to distinguish output from demand, which is often difficult with macro-economic data.

On the other hand, using this type of survey data has a number of problems. First, the survey results are aggregated across firms, preventing comparisons of individual firms' expectations and outcomes. The second problem is the conversion of the qualitative survey data into a form that can be used in quantitative analysis. The most commonly used procedure for this type of survey data is to use the “balance statistic” (Theil (1952)). This statistic is defined as the difference between the proportion of firms experiencing (expecting) an increase in the relevant variable and the proportion experiencing (expecting) a fall. If movements in this statistic are to accurately reflect movements in the underlying series, a number of restrictive assumptions must be satisfied.^[7] These include that the underlying series (say price changes) has a constant variance and is uniformly distributed across firms. Furthermore, the threshold level at which firms report that a change has occurred must be constant through time and across firms.

A number of modifications of the balance statistic have been proposed. The two most widely used were developed by Carlson and Parkin (1975) and Pesaran (1985). The Carlson and Parkin method involves computing the sample mean and variance from the aggregated response data, making explicit assumptions about the distribution followed by the underlying series. Pesaran adopts a regression-based approach which involves estimating the appropriate weights on the “increase” and “decrease” responses when calculating the net balance statistic. The details of these and other more complicated procedures are discussed in Pesaran (1987) and Smith and McAleer (1990).

Unfortunately, a consensus has not been reached as to which is the superior method of quantification. Pesaran (1987) argues that the appropriate summary statistic depends upon the particular circumstances being investigated, but that many of the approaches yield very similar estimates and conclusions. Other studies have been even less conclusive. Defris and Williams (1979) and Batchelor (1986), compared the results of surveys which used quantitative expectations of price movements with those using summary measures calculated from qualitative surveys. They found that the balance statistic and the Carlson-Parkin mean tracked the year-to-year movements in average expectations reasonably well, but not shorter-term movements. In empirical work, however, the balance statistic was found to be systematically biased, and led to an incorrect rejection of the hypothesis of rationality.

Smith and McAleer (1990) used the ACCI/Westpac data to compare the properties of the various statistics. Their focus was on which measure was most useful in a forecasting context and on determining whether the broad conclusions concerning rational expectations were robust to alternative procedures. While they found a lack of robustness across different procedures, they did conclude that all of the measures provided information which was useful for forecasting.

An additional potential problem arises from the fact that the balance statistic (and many of its variations) is bounded. The balance statistic must lie between negative and positive one hundred. As a result, the dependent variable in many of our regressions is not normally distributed and may be truncated. This is essentially the same problem as the one encountered with the modelling of frequency data, and thus the same issues concerning the relative merits of linear probability and probit models are relevant here.^[8] In our case there are unlikely to be any benefits from using a non-linear estimation technique which takes account of these constraints, as the simple OLS regressions that we report do not yield any predicted values outside the −100 to 100 range.

Keeping the potential short comings in mind, we use the balance statistic to convert qualitative data to quantitative data in this paper.^[9] The correlation between the net balance statistic for output and the quarterly change in manufacturing output (from the national accounts) is 0.47, while the correlation between the net balance statistic for prices and quarterly changes in the prices of goods produced by manufacturers is 0.68. The alternatives to the balance statistic did not generate consistently higher correlations. In addition, a regression of the Hodrick-Prescott adjusted output gap for the manufacturing sector on the survey measure of capacity utilisation produced a positive coefficient, with a t-statistic of 8.33 and an 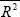of 0.51.

Footnotes

This question was changed into its current form in December of 1987. The question had previously asked firms: “Are you operating at a satisfactorily full rate of operation? Yes/No”. The change in the nature of the question does not appear to lead to a break in the series, nor does it appear to affect the behaviour of the series or any of the results reported in the following section. [5]

See Flood and Lowe (1993) for a more detailed discussion of this issue. [6]

See Batchelor (1986) pp. 103–5 and p. 108 and references cited therein. [7]

See Konig and Nerlove (1983) and Zimmerman (1986) for examples of the use of log linear probability models. Heckman (1978) and Hausman and Wise (1978) discuss the relative merits of their use. [8]

To examine the sensitivity of choosing the net balance statistic method over alternative statistics the regressions corresponding to Tables 2, 5 and 6 were conducted using the ratio of net balance to no change responses (see Pesaran (1987)). The results were not qualitatively different from those obtained using the net balance statistic. Details of these regressions are available from the authors. [9]