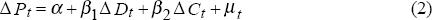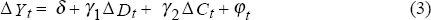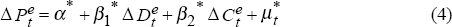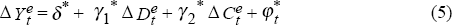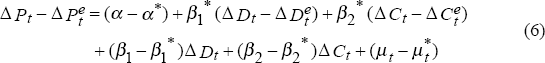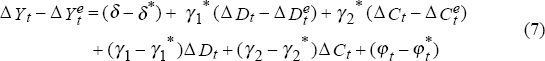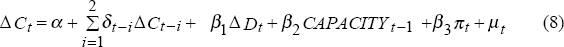RDP 9411: Demand Shocks, Inflation and the Business Cycle 4. The Links Between Demand, Costs, Prices, and Output
December 1994
- Download the Paper 72KB
This section is divided into two parts; the first outlines our empirical strategy and the second presents and discusses the results.
4.1 The Empirical Framework
We begin by modelling actual price and output changes as a function of changes in demand and costs. Using the simplest specification we can write:
where P denotes the average selling price, D new orders received, C the average cost per unit of output and Y the level of output.
We can write analogous equations for firms' expectations of price and output changes. These equations can be estimated as the survey asks firms about their expected outcomes.
Where superscript e denotes the expected value of the relevant variable.
We can also estimate equations explaining unexpected changes in prices and output, in terms of unexpected changes in demand and costs. The unexpected changes are derived simply by subtracting the expected change from the actual change:
This framework allows us to examine the impact of changes in costs and demand on prices and output. If an increase in demand leads to higher prices through an increase in margins (given costs) then we should see a positive coefficient on the actual, expected and unexpected changes in demand in equations (2), (4) and (6) respectively. If the impact of changes in demand on prices works solely through a change in costs, then the change in demand should not be a significant explanator of the change in prices. Similarly, if an increase in production costs leads to an increase in output prices, the coefficient on the actual, expected and unexpected change in costs in equations (2), (4) and (6) respectively, should be positive and significant.
If higher production costs also lead to a decline in output, γ2 and 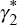 should be negative and significant, while
if higher demand generates an increase in output, γ1
and
should be negative and significant, while
if higher demand generates an increase in output, γ1
and 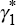 should be positive and significant.
should be positive and significant.
We suggested in Section 2 that the output and price responses may be a function of the level of capacity. To allow for the possibility that changes in demand have differential effects on output and prices depending upon whether firms are above or below capacity, we allow the β and γ coefficients to vary, depending on whether or not a positive net balance of firms is operating above normal capacity. This is done by introducing dummy variables into the various equations. These dummy variables allow the slope coefficients to vary with the level of capacity utilisation.
A similar procedure is followed to allow for asymmetric effects of changes in costs on prices. Here, however, the interaction between costs, prices and capacity is a little more difficult to capture. The coefficient on costs is, in a sense, the pass-through parameter – that is, given that a number of firms are experiencing an increase in costs, how many are putting up their prices. It may well be the case that the degree of pass-through does not depend on capacity, but rather that the number of firms actually experiencing a cost increase is a function of the level of capacity utilisation. To examine this possibility we directly examine the effect that capacity has on cost changes.
When there is high background inflation, more firms will be putting their prices up for a given increase in demand, than would be the case in a low-inflation environment. To control for the effect of background inflation, we initially include the 12-month-ended percentage change in the Private Consumption Deflator in the equations explaining actual changes in prices and output.[10] Where it is insignificantly different from zero we remove it from the specification and re-estimate the model. In the “expected” and “unexpected” equations, we include expected and unexpected inflation where the expected rate of inflation is estimated from a simple AR(4) model.
Lags of the relevant dependent variable are also included in the estimated specifications. These are included to capture the fact that price and output responses to changes in demand and costs may not be instantaneous. In both equations (2) and (3) four lags are initially included and then insignificant lags are excluded sequentially. In both equations this procedure results in just one lag being included. The same specification is then used for the “expected equations”. In the unexpected equations, if the same model describes actual and expected outcomes, then the lagged level of price changes (or output changes), the constant and the contemporaneous changes in demand and costs should not enter the equation. We do however include these variables and test the hypothesis that the coefficients are jointly equal to zero (the constant term is excluded from these tests).
While the ACCI/Westpac Survey was first conducted in 1961, questions concerning costs were not introduced until June 1966. Thus our sample period starts at the third quarter of 1966 and runs until the second quarter of 1994, giving a total of 112 observations.
The 6 equations comprising the price and output equations are estimated jointly using the SUR technique. The structure of the equations means that the residuals within each block (that is, the price block and the output block) are closely related – at least conceptually, the residuals from the “unexpected change” equation are equal to the residuals from the “actual change” equation less the residuals from the “expected change” equation. While this implies a particular structure to the variance-covariance matrix, this structure is not imposed, and the matrix is estimated freely. The SUR technique also takes into account the correlation between residuals in the price and output equations – the highest correlation is 0.23 and is between the residuals in the equations for unexpected price changes and unexpected output changes.
Basic descriptive statistics for actual, expected and unexpected changes in prices, output, demand and costs are reported in Appendix 1.
4.2 The Results
4.2.1 The Price Response to Changes in Demand and Costs
The estimation results for equations (2), (4) and (6) are presented in Table 2.
| Actual Change | Expected Change | Unexpected Change | |
|---|---|---|---|
| Constant | −15.03** (−8.33) |
−3.85* (−2.27) |
−11.28** (−7.40) |
| Change in Pricet−1 | 0.32** (5.50) |
0.37** (6.88) |
−0.05 (−1.03) |
| Actual Change in Demand | 0.20** (8.41) |
0.09** (3.87) |
|
| Actual Change in Costs | 0.51** (10.73) |
0.00 (0.00) |
|
| Expected Change in Demand | 0.11** (4.53) |
||
| Expected Change in Costs | 0.51** (9.51) |
||
| Unexpected Change in Demand | 0.12** (5.06) |
||
| Unexpected Change in Costs | 0.53** (10.27) |
||
| Actual Inflation Rate | 1.15** (3.78) |
0.86** (3.41) |
|
| Expected Inflation Rate | 0.28 (1.07) |
||
| Unexpected Inflation Rate | 0.12 (0.40) |
||
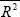 |
0.92 | 0.92 | 0.60 |
| Hypothesis Test: | |||
| Actual Variables in Unexpected Equation are jointly zero | 31.39 {0.00} |
||
| Notes: The test that the coefficients on the actual variables (that is, the lagged change in actual price, actual changes in demand and costs and the actual inflation rate) in the unexpected price equation are jointly zero excludes the constant term. t-statistics are reported in parentheses – **(*) indicates that the coefficient is significantly different from zero at the 1%(5%) level. Numbers in {} are p-values. | |||
Clearly, both demand and cost factors are important in generating increases in output prices. Given the number of firms that report a change in costs, the higher the number of firms that report an increase in demand, the higher the number of firms that report an increase in prices – that is, demand and margins move together positively. In the equation explaining actual price changes, the coefficient on the actual change in demand is positive and significant. Similarly, the greater the number of firms that expect an increase in demand, the greater the number of firms that expect to increase their prices. Finally, when firms find that demand is unexpectedly strong, they appear to increase their prices by more than they had initially intended, even after accounting for any unexpected increase in costs.
Changes in costs also play an important role in firms' decisions to change prices. The estimates suggest that if an additional 10 firms report an increase in costs (and demand is unchanged), 5 of those firms will increase their price in the same quarter. This is regardless of whether the cost increase is expected or unexpected. However, not all the adjustment in prices occurs in the same quarter as the increase in demand and costs. The final response is around 1.5 times the initial effect.
Over the sample period the average number of firms reporting an increase in costs in a particular quarter is greater than the average number reporting an increase in prices; the average net balance statistic for changes in prices is +32, while that for costs is +56. This does not mean that costs increased faster than prices. Rather it reflects the fact that a change in just one of a firm's cost components leads the firm to report an increase in costs. If this component is small, and the resulting increase in total costs is also small, the firm may not increase its output price, preferring instead to wait until it experiences a larger increase in costs. As a result, more firms report increases in costs than increases in prices. This is consistent with the Ss pricing models.[11] In these models, the existence of costs to changing prices (“menu costs”) means that firms will only change prices when the actual price has moved a specified amount away from the optimal price. It is also worth noting that the percentage of firms reporting a change in prices averaged 50 per cent over the sample period, and in some quarters as few as 16 per cent of firms reported “no change”. This suggests that, when necessary, firms are prepared to change prices relatively frequently.
The results also confirm that the initial impact of changes in demand and costs on prices is less than the eventual impact. In addition, the higher is the background inflation rate, the greater will be the number of firms increasing their prices in any given quarter. Unexpectedly high inflation, however, does not seem to be associated with an unexpectedly large number of firms putting up their prices in the same quarter.
The hypothesis that the coefficients are the same in the equations explaining actual and expected price change is clearly rejected. The constant in the regression explaining unexpected price changes is negative and significant. The net balance of firms that expect to be able to increase their prices is systematically larger than the net balance actually reporting an increase in prices. This optimism is also reflected in expectations of output where, on average, the average net balance of firms recording an increase in demand is less than the average net balance expecting an increase in demand (see Appendix 1).
The table also reports the result of testing the hypothesis that the coefficients on lagged actual changes in price, actual inflation and actual changes in demand and costs are jointly zero in the equation explaining unexpected changes in price. The hypothesis is clearly rejected. In particular, the coefficient on actual changes in demand in the equation explaining actual price changes is significantly higher than the coefficient on the unexpected change in demand in the equation explaining unexpected price changes. This suggests that, systematically, the actual realisation of a change in demand has a greater effect on prices than was anticipated.
We now turn to an examination of how capacity constraints influence the price response to a change in demand. As was discussed above, this is done by allowing different price responses depending upon whether a net balance of firms is reporting that they are operating above or below capacity. In the sample used, 26 of the 112 observations are characterised by production in excess of normal capacity.[12] The estimation results are reported in Table 3.
| Actual Change | Expected Change | Unexpected Change | |
|---|---|---|---|
| Constant | −13.95** (−7.94) |
−2.24 (−1.35) |
−11.75** (−7.87) |
| Change in Pricet−1 | 0.34** (5.83) |
0.41** (7.75) |
−0.07** (−1.35) |
| Actual Change in Demand | |||
| Above Normal Capacity | 0.06 (1.33) |
0.07 (1.56) |
|
| Below Normal Capacity | 0.24** (8.53) |
0.09** (3.62) |
|
| Actual Change in Costs | |||
| Above Normal Capacity | 0.51** (10.40) |
0.04 (0.74) |
|
| Below Normal Capacity | 0.50** (10.35) |
0.00 (0.06) |
|
| Expected Change in Demand | |||
| Above Normal Capacity | −0.01 (−0.16) |
||
| Below Normal Capacity | 0.14** (5.38) |
||
| Expected Change in Costs | |||
| Above Normal Capacity | 0.47** (8.42) |
||
| Below Normal Capacity | 0.49** (9.60) |
||
| Unexpected Change in Demand | |||
| Above Normal Capacity | 0.01 (0.26) |
||
| Below Normal Capacity | 0.15** (5.38) |
||
| Unexpected Change in Costs | |||
| Above Normal Capacity | 0.49** (6.42) |
||
| Below Normal Capacity | 0.51** (9.97) |
||
| Actual Inflation Rate | 1.09** (3.62) |
0.95** (3.80) |
|
| Expected Inflation Rate | 0.10 (0.40) |
||
| Unexpected Inflation Rate | −0.08 (−0.24) |
||
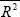 |
0.93 | 0.93 | 0.60 |
| Hypothesis Tests: | |||
| Actual Variables in the Unexpected Equation are Jointly Zero | 39.53 {0.00} |
||
| Demand Effect Independent of Capacity | 7.60 {0.01} |
||
| Cost Effect Independent of Capacity | 0.10 {0.75} |
||
| Notes: The test that the coefficients on the actual variables in the unexpected equation are jointly zero excludes the constant term. t-statistics are reported in parentheses – **(*) indicates that the coefficient is significantly different from zero at the 1%(5%) level. Numbers in {} are p-values. | |||
In the equation explaining actual price changes, the coefficient on changes in demand when output is above capacity is small and insignificantly different from zero. In contrast, the coefficient on changes in demand when most firms are operating below capacity is positive and significant. These results suggest that changes in demand have their greatest impact on manufacturers' margins when output is below capacity. It does not appear to be the case that extremely high levels of demand (relative to capacity) put significant upward pressure on margins. Instead, the principal downward (upward) pressure on margins comes when demand is already low and falling (rising) – such periods are usually associated with recessions. A similar picture emerges from the equation explaining expected price changes: when the number of firms expecting demand to increase is relatively high, firms do not expect to increase their prices by more than the change in costs would have suggested.
To gain further insight into the relationship between margins and capacity we split the sample again. First, we distinguish between periods when more firms report that demand is rising than falling. We then cross-classify the observations by the degree of excess capacity. Three cases are used: no excess capacity (the net balance capacity variable is greater than or equal to zero), normal excess capacity (net balance between −45 and 0) and high excess capacity (net balance equal to or less than −45). To control for the effect of costs on prices, we regress the price change variable on a constant, its own lagged value, the cost change variable and inflation. The residuals from this regression represent price changes that are not explained by changes in costs; one interpretation is that they represent the direct demand effects on prices. A negative residual implies that fewer firms raised prices than was predicted by the simple model which excludes demand, while a positive residual implies that a greater number of firms raised prices than can be explained by this simple model. The average residual for each of our six (2×3) categories is presented in Table 4.
|
High Excess Capacity |
Normal Excess Capacity |
No Excess Capacity |
|
|---|---|---|---|
| Rising Demand | 5.30 (6) |
2.69 (37) |
1.66 (22) |
| Falling Demand | −6.02 (19) |
−2.36 (24) |
0.81 (4) |
| Note: Numbers in parentheses indicate the number of observations in each category. | |||
Clearly, the most significant downward pressure on margins comes when demand is falling and there is already a large amount of excess capacity – the average residual in this case is −6.02. A fall in demand appears to have a larger effect on prices (independent of the cost channel), the higher is the level of excess capacity. The results also indicate that when many firms have high excess capacity, but more firms are reporting rising rather than falling demand, then the number of firms putting up prices will be greater than that suggested by the number of firms experiencing an increase in costs. This suggests that it is not only the level of excess capacity that influences the decision to change margins, but also the direction of change in demand. Even when there is considerable excess capacity, provided demand is increasing, firms appear to be willing to rebuild the margins that were squeezed as demand fell. Once capacity utilisation has recovered to levels approaching “normal”, further increases in demand appear to lead to smaller increases in margins.
These results suggest that both the level of demand (relative to capacity) and the change in demand are important for understanding the behaviour of margins in the manufacturing sector. While the size of margins is positively correlated with the level of the output gap, most of the movement in margins takes place in recessions, when margins narrow when demand is falling and then widen as demand begins to increase.[13]
Do these results throw any light on the various theories explaining markups? It may well be that there are two countervailing forces. The customer markets theory suggests that when demand is high, the value to a firm of maintaining its customer base declines. As a result, firms will be willing to increase their margins and their profits; this phenomena is sometimes described by the somewhat colourful term “price gouging”. Opposing this force is the idea that when demand is strong, competitive pressures increase and firms increase prices by less than the increase in costs. In addition, if a firm believes that demand is going to be strong for only a relatively short period of time, it may not be prepared to “gouge” its customers, for fear that the customers will leave them permanently.
When demand is very low, the picture seems a little different. In this case, the customer markets explanation appears to dominate. Faced with falling demand, firms find it attractive to engage in discounting to keep existing customers and to attract new customers who will be likely to stay with the firm in the up-swing. This leads to a narrowing of margins. In addition, faced with low and falling demand, firms are likely to have heightened concerns about their ability to survive. Such concerns may also lead to discounting. Once demand starts increasing, although the level of demand is low, discounting appears to lessen. If the initial increases in demand indicate a period of continuing demand growth, concerns about survival and the need to attract new customers through price reductions decline. The result is that most rebuilding of margins appears to be done in the early stage of the recovery.
While the effect of a demand change on prices appears to depend upon the level of capacity utilisation, the results in Table 3 suggest no such dependence for the pass-through of a cost increase to prices. The coefficients on the change in cost variable do not depend upon the level of capacity – the coefficients are not significantly different from one another and are quite close in magnitude. This is the case in both the actual and unexpected price change equations. As discussed earlier, this does not mean that capacity constraints have no influence on prices through costs, for the level of capacity may influence the number of firms reporting a cost increase, while having no influence on the pass-through of any given cost increase. To test this proposition we estimate the following equation for the actual change in costs:
where CAPACITY is the net balance of the capacity variable and π is the inflation rate. The estimation results are presented in Table 5.
| Actual | |
|---|---|
| Constant | 6.13** (2.62) |
| Change in Costst−1 | 0.66** (8.02) |
| Change in Costst−2 | 0.14* (2.02) |
| Actual Change in Demand | 0.03 (0.88) |
| Capacityt−1 | 0.13** (3.63) |
| Actual Inflation | 0.95** (3.65) |
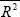 |
0.89 |
| Notes: t-statistics are reported in parentheses – **(*) indicates that the coefficient is significantly different from zero at the 1%(5%) level. | |
The level of capacity is a significant explanator of the change in costs. The higher the number of firms reporting that they are operating at normal or above capacity at the beginning of the quarter, the greater will be the number of firms registering increases in average costs during the quarter. An increase in demand during the quarter, however, appears to have no additional effect on costs – the coefficient on the actual change in demand is small and insignificantly different from zero. As was the case for margins, the level of demand seems to matter, but unlike the margins case, the number of firms reporting changes in demand in a particular quarter seems to have little direct impact.
The estimates also suggest that the full impact on costs is substantially greater than the initial effect: a movement of five firms from reporting that they are operating below capacity to reporting that they are operating above capacity (a change in the net balance of 10) will lead to just one (10 × 0.13) additional firm recording an increase in costs in the same quarter. However, at the end of four quarters, an additional 4 firms will have reported an increase in costs. One way to interpret this lagged response is that capacity constraints lead to higher costs through increases in factor costs, but that factor costs increase with some lag, perhaps due to the time taken to re-negotiate contracts. The earlier results suggested that once the cost increases have taken place they are passed through to prices relatively quickly, although again the eventual price response is larger than the initial response.
Similar to the results for prices, the results show that an increase in general inflation leads to more manufacturing firms experiencing an increase in costs.
4.2.2 The Output Response to Changes in Demand and Costs
We now turn to the effect of changes in demand and costs on output. The estimation results for equations (3), (5) and (7) are presented in Table 6.[14]
| Actual Change | Expected Change | Unexpected Change | |
|---|---|---|---|
| Constant | 6.79** (4.72) |
2.15 (1.33) |
4.49** (2.63) |
| Change in Outputt−1 | 0.12** (2.81) |
0.21** (6.04) |
−0.09* (−2.02) |
| Actual Change in Demand | 0.75** (19.80) |
0.01 (0.33) |
|
| Actual Change in Costs | −0.05* (−2.28) |
−0.09** (−3.23) |
|
| Expected Change in Demand | 0.74** (20.94) |
||
| Expected Change in Costs | 0.04 (1.39) |
||
| Unexpected Change in Demand | 0.72** (19.96) |
||
| Unexpected Change in Costs | 0.04 (1.03) |
||
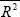 |
0.93 | 0.89 | 0.60 |
| Hypothesis Test: | |||
| Actual Variables in the Unexpected Equation are Jointly Zero | 17.08 {0.00} |
||
| Notes: The test that the coefficients on the actual variables (that is, the lagged change in output and the actual changes in demand and costs) in the unexpected output equation are jointly zero excludes the constant term. t-statistics are reported in parentheses – **(*) indicates that the coefficient is significantly different from zero at the 1%(5%) level. Numbers in {} are p-values. | |||
Clearly, the number of firms reporting demand changes is of critical importance in determining the number of firms reporting output changes – the coefficient on the actual change in demand is large and highly significant. Similarly, the greater the number of firms that expect an increase in demand, the higher the number of firms expecting output to increase. When more firms experience a demand increase than expected, this translates into a higher number of firms experiencing output increases than had been expected. These results suggest that when firms experience an increase in demand, they are able to change output relatively quickly, with most of the output response occurring in the same quarter as the demand change.
The evidence on the impact of changes in costs on output is mixed and difficult to interpret. On the one hand, actual changes in costs do appear to have a role in influencing firms' actual production decisions. The more firms experiencing a cost increase, given the change in demand, the smaller the number of firms experiencing an increase in output. The effect is, however, quite small. On the other hand, if more firms are expecting an increase in costs, there is no evidence that this makes more firms pessimistic about their output decisions. Similarly, the results for the equation explaining unexpected changes in output suggest that cost shocks play no significant role in explaining unexpected changes in output.
Again, we reject the restriction that the coefficients on the actual variables in the unexpected output equation are jointly zero. In addition to the fact that the effect of costs differs in the actual and expected equations, firms seem to place greater weight on the previous change in output when forming their forecasts of future changes in output than is actually warranted. This is suggested by the negative coefficient on the lagged change in output in the equation explaining the unexpected change in output.
We now turn to examining the link between changes in output and capacity. Work by Shapiro (1989) using the US Federal Reserve's Capacity Utilisation Index finds no evidence in support of the idea that high levels of capacity utilisation limit output expansion. Shapiro concludes that one possible explanation is that supply is very elastic, and that periods of high demand and output are typically periods of low-cost production. In contrast, the results reported in Table 7 suggest that capacity constraints do limit the output response to changes in demand. The table contains results of regressions which allow for different output responses to changes in demand and costs, depending upon whether a net balance of firms is operating above or below capacity.
Again, the first column explains actual output changes. When a net balance of firms is operating above normal capacity, a change in demand generates a smaller increase in output than is the case when a net balance of firms is operating below normal capacity. This difference is significantly different from zero at the 1 per cent level, and indicates that capacity constraints do bind, limiting the output response (at least, in the short run) to rising demand.[15] A similar result is suggested by the expected output equation – a greater number of firms expect an increase in output, given the number that expect an increase in demand, when demand is below capacity than when it is above capacity. There appears to be no asymmetry in the impact of changes in costs on the decision to change output.
| Actual Change | Expected Change | Unexpected Change | |
|---|---|---|---|
| Constant | 7.59** (5.55) |
2.93 (1.91) |
4.41** (2.99) |
| Change in Outputt−1 | 0.11* (2.55) |
0.17** (4.47) |
−0.05 (−1.26) |
| Actual Change in Demand | |||
| Above Normal Capacity | 0.57** (10.93) |
0.05 (0.86) |
|
| Below Normal Capacity | 0.80** (20.32) |
−0.02 (−0.53) |
|
| Actual Change in Costs | |||
| Above Normal Capacity | −0.04 (−1.33) |
−0.12** (−3.57) |
|
| Below Normal Capacity | −0.06* (−2.50) |
−0.07** (−2.80) |
|
| Expected Change in Demand | |||
| Above Normal Capacity | 0.54** (9.90) |
||
| Below Normal Capacity | 0.83** (22.01) |
||
| Expected Change in Costs | |||
| Above Normal Capacity | 0.10** (2.66) |
||
| Below Normal Capacity | 0.01 (0.55) |
||
| Unexpected Change in Demand | |||
| Above Normal Capacity | 0.46** (7.98) |
||
| Below Normal Capacity | 0.82** (20.69) |
||
| Unexpected Change in Costs | |||
| Above Normal Capacity | 0.02 (0.21) |
||
| Below Normal Capacity | 0.03 (0.69) |
||
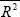 |
0.93 | 0.90 | 0.68 |
| Hypothesis Tests: | |||
| Actual Variables in the Unexpected Equation are Jointly Zero | 21.89 {0.00} |
||
| Demand Effect Independent of Capacity | 30.58 {0.00} |
||
| Cost Effect Independent of Capacity | 0.02 {0.89} |
||
| Notes: The test that the coefficients on the actual variables (that is, the lagged change in actual output and the actual changes in demand and costs) in the unexpected output equation are jointly zero excludes the constant term. t-statistics are reported in parentheses − **(*) indicates that the coefficient is significantly different from zero at the 1%(5%) level. Numbers in {} are p-values. | |||
Footnotes
To allow for the possibility that firms adjust their prices in response to changes in manufacturing prices we re-estimate these equations using the four-quarter change in manufacturer's output prices. As these data are available over a shorter sample period we re-estimate the equations over the shorter period for both measures of inflation. The results are not qualitatively different. [10]
For example see Barro (1972), Caplin and Sheshinski (1987), Sheshinski and Weiss (1983) and Caplin and Leahy (1991). [11]
There are 3 cases in which the net balance for the capacity variable is zero. These are included in the “above normal” capacity category. We also used an alternative estimate of full capacity; that is, full capacity was defined to occur when the net balance statistic was greater or equal to −10. This expanded the number of cases of above normal capacity to approximately one third of the sample. All qualitative results remained unchanged. [12]
The correlation between the change in margins (that is, the residuals used in Table 4) and the change in the Hodrick-Prescott measure of the output gap is 0.38 (t-statistic of 3.31). The correlation is 0.42 with a t-statistic of 3.74 for the trend-adjusted measure. These correlations are estimated over the period 1977 quarter 3, to 1994 quarter 2. [13]
The inflation rate is excluded as the coefficient was found to be insignificantly different from zero. [14]
When the equations for unexpected changes in prices and output were estimated jointly, but without the equations for actual and expected outcomes in the system, the results were essentially unchanged. The largest change occurred in the equation explaining unexpected output changes. In this less restricted system, the asymmetry in the effect of demand shocks was considerably larger, with the coefficient on unexpected changes in demand when capacity is above normal falling to 0.25. [15]