RDP 9608: Modelling the Australian Exchange Rate, Long Bond Yield and Inflationary Expectations Appendix C: The Behavioural Model of Australian Long Bond Yields – Integration Tests and Diagnostics
November 1996
- Download the Paper 171KB
| H0: Non-stationarity | H0: Stationarity | ||||||
|---|---|---|---|---|---|---|---|
| Φ3 | ττ | τμ | DF-GLSτ | DF-GLSμ | KPSSτ | KPSSμ | |
| Real 10-yr bond | 10.51*** | −4.37*** | −4.31*** | −11.24*** | −11.94*** | 0.08 | 0.43* |
| Real US 10-yr bond | 4.38 | −2.94 | −2.63 | −1.21 | −1.46 | 0.12* | 0.12 |
| Return on capital | 6.29** | −3.53** | −3.49** | −3.56** | −3.60*** | 0.10 | 0.19 |
| Cash rate | 2.47 | −1.96 | −1.42 | −5.29*** | −5.90*** | 0.16** | 0.28 |
| Government deficit | 5.14 | −3.18* | −3.19** | −2.64 | −2.56** | 0.11 | 0.11 |
| Undiversifiable risk | 1.36 | −1.60 | −1.52 | −6.52*** | −7.46*** | 0.12* | 0.13 |
| Current account | 3.54 | −2.21 | −2.68 | −3.39** | −5.54*** | 0.21** | 0.51** |
| Inflation expectations | 12.03*** | −4.89*** | −2.80 | −3.68** | −2.15** | 0.07 | 0.39* |
| Δ Inflation | 58.8*** | −10.80*** | −10.84*** | −1.79 | −0.77 | 0.08 | 0.11 |
|
Notes: *, ** and *** denote significance at the 10%, 5% and 1% levels respectively. Φ3 refers to the likelihood ratio test of (α, β, ρ)=(α, 0, 1) in Yt = α + βt + ρYt−1 + et. The critical values are from Dickey and Fuller (1981). τ refers to the Augmented Dickey-Fuller (ADF) ‘t-tests’; ττ includes a constant and trend and τμ includes a constant only. The critical values are from Fuller (1976). DF – GLSτ and DF – GLSμ are a modified trend and constant version, respectively, of the ADF tests proposed by Elliot et al. (1992). KPSS is a test proposed by Kwiatkowski et al. (1992) which tests the null hypothesis of stationarity. A truncation lag of 8 is used for the calculation of the estimate of the error variance. |
|||||||
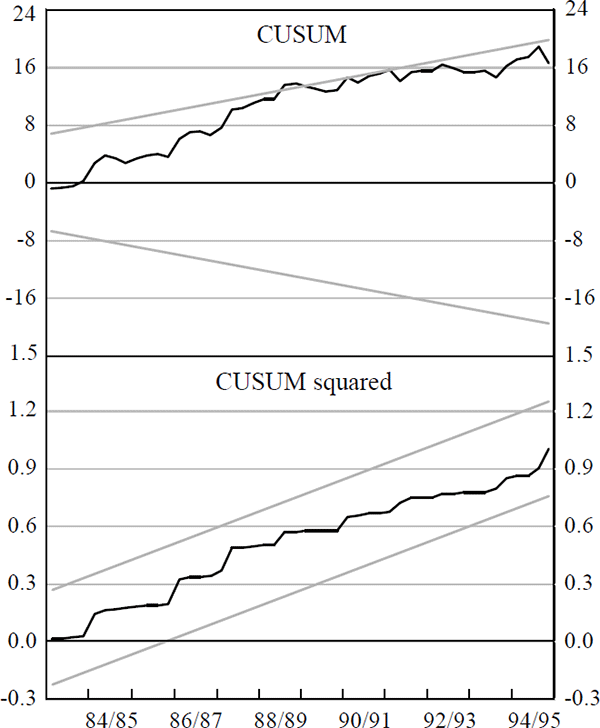
All three tests support the stationarity of the Australian real 10-year bond rate around a constant or a trend. On the other hand, evidence for the US real long bond rate is mixed; the ADF and DF-GLS tests fail to reject their null of a unit root, but the KPSS test fails to reject the null hypothesis that the US real long bond rate is stationary around either a mean or a trend. The return on domestic capital and inflationary expectations are both clearly stationary; the ratio of the Commonwealth government budget balance to GDP is mean stationary; the evidence for the undiversifiable risk term, ‘beta’, is mixed.
| Explanatory variable |
Coefficient (Standard error) |
|---|---|
| Speed of adjustment parameter | −0.513*** (0.10) |
| Return on capital | 0.164*** (0.04) |
Inflation term : 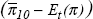 |
0.256*** (0.08) |
| Δ Real bondt−2 | 0.369*** (0.12) |
| Δ Return on capitalt−1 | 0.431* (0.23) |
| ΔEt (π) | −1.22*** (0.22) |
| Δ Et–2 (π) | 0.93 *** (0.29) |
| Δ Government deficitt | 0.89* (0.52) |
| Growtht | 0.40* (0.21) |
| Growtht−1 | −0.39* (0.20) |
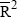 |
0.60 |
| DW | 1.76 |
ARCH test 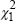 |
0.882 [0.347] |
AR (4) test 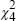 |
3.28 [0.512] |
Jarque-Bera Normality test 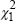 |
0.96 [0.618] |
|
Notes: *, ** and *** denote significance at the 10%, 5% and 1% respectively. Standard errors are in parentheses; probability values are in square brackets. |
|
| Nominal Bondt−1 | −0.241*** (0.055) |
|---|---|
| Return on Capitalt−1 | 0.079*** (0.029) |
| US Real Ratet−1 | 0.127* (0.67) |
| Perfect Foresight 1-year-aheadMarkov Expectationst−1 | 0.204*** (0.042) |
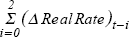 |
0.268* {0.084} |
| Δ Markov Expectationst−1 | −0.375*** (0.136) |
| Δ GDPt−3 | −0.304*** (0.111) |
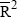 |
0.332 |
| DW | 2.07 |
ARCH test 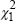 |
0.416 [0.519] |
AR (4) test 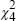 |
3.0846 [0.544] |
Jarque-Bera Normality test 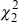 |
1.408 [0.495] |
|
Notes: *, ** and *** denote significance at the 10%, 5% and 1% respectively. Standard errors are in brackets (), probability values are in square brackets and the F-test for the joint significance of the US real rate dynamics are in parenthesis. |
|
The small negative coefficient on the third lag of growth in the dynamics of equation (7) corresponds with the (roughly) three-year cycle in bond yields in Australia.