RDP 9608: Modelling the Australian Exchange Rate, Long Bond Yield and Inflationary Expectations 2. The Macroeconomic Model Approach

This section focuses on two widely quoted macroeconomic models of the Australian economy: the Murphy model and the TRYM model.^[1] These macro models embody similar philosophies, sharing many common features of design and specification. They have similar theoretical underpinnings, with Keynesian properties in the short run (prices are sticky and output is demand-determined) and neoclassical properties in the long run. Equations describing the exchange rate and the long-term bond yield are elements of the financial sectors of these models and reflect orthodox theoretical considerations; they are not estimated behavioural equations. This section briefly discusses these two financial sector equations and their implied responses to shocks.

The process of expectations formation is central to the performance of the macro-model equations. Financial sector expectations are typically assumed to be model-consistent. In particular, inflation expectations are constructed from some combination of the current inflation rate and the equilibrium inflation rate which is derived from the steady-state version of the model. The equilibrium inflation rate is secured in the long run by assuming that the authorities have an exogenously-determined target for some nominal variable. In TRYM, the authorities target the money growth path; in recent versions of the Murphy model, a nominal income target is specified. The equilibrium inflation rate is then that rate which is consistent with the difference between money supply (nominal income) and real output growth in the long run.

In the Murphy model, quarterly inflationary expectations are then calculated from a weighted average of current inflation and the model's one-quarter-ahead predicted long-term equilibrium inflation rate. In TRYM, inflationary expectations are evaluated as the average rate of inflation over the next ten years as implied by the difference between the current level of prices and the equilibrium price level in period t+40 quarters.

2.1 Exchange Rate Determination

Each of the macro models employs a concept of the equilibrium real exchange rate. This is defined as that rate which achieves macroeconomic (that is, simultaneous internal and external) balance; it is calculated by a calibration of the steady-state version of the model prior to any dynamic simulation. In this way, the equilibrium exchange rate reflects the specification of interactions within the individual macroeconomic model. In TRYM, for example, adjustment back to the equilibrium rate, following any shock, is assumed to be complete within 40 quarters.

After tying down the long-run real equilibrium exchange rate, current and future changes in the real exchange rate are determined by an uncovered interest parity condition – if foreign long (10-year) interest rates are above domestic rates, the current value of the exchange rate must be below its equilibrium value. In the long run, the interest differential collapses (either to zero or, alternatively, to some constant risk premium).

The macro-models' equilibrium exchange rate is akin to the concept of the so-called fundamental equilibrium exchange rate (FEER), popularised by Williamson in the early 1980s. It realises internal balance, interpreted in the standard way, as achieving the underlying level of potential output which is consistent with the NAIRU. External balance is more difficult to define, and In't Veld (1991), in calculating equilibrium exchange rates for each of the G3 countries, found that his results were very sensitive to changes in this definition. The concept is intended to describe an equilibrium position in the current account; in the Australian macro models this is achieved with a stable ratio of foreign liabilities to GDP (typically stabilised at around 45 per cent, a little higher than the current level).^[2] As with any intertemporal analysis, the path to external balance depends on current assessments of the future values of variables. The part of the macroeconomic model that is critical in this exercise is the trade sector which consists of equations expressing the dependence of output and the balance of payments on demand and competitiveness (the real exchange rate). For example, the present discounted value of future terms of trade shocks impacts upon the current exchange rate to the extent that it moves the equilibrium exchange rate in the long run; the equilibrium exchange rate moves to offset income effects on the current account and restore external balance.

Bayoumi, Clark, Symansky and Taylor (1994) conducted sensitivity analysis on the macroeconomic models of several industrial economies. They found that the estimated range in the calculated equilibrium exchange rates varied between 10 and 30 per cent. This degree of imprecision implies that interpretation of such an equilibrium rate is perhaps better restricted to the identification of relatively large exchange rate misalignments. Furthermore, the calculation of equilibrium real exchange rates as a basis for policy depends on an analysis of whether there are predictable shifts in the real exchange rate and the extent to which different sources of these shifts can be disentangled (for example, structural changes from long-lag dynamics). This is an exercise more appropriately undertaken in the behavioural framework outlined in Section 3.

2.2 Interest Rate Determination

Consistent with traditional textbook models, the short-term interest rate in these macro models is endogenous. As discussed above, the authorities are assumed to target an exogenously-determined nominal variable. In TRYM, for example, where this target variable is the money-growth path, a simple error-correcting money demand equation describes the link between the model's financial and real sectors. TRYM goes some way towards recognising the role of the short-term interest rate as the policy instrument by inverting the long-run component of this estimated money demand equation. This produces what might be broadly interpreted as a rate-setting monetary policy rule: the current level of the short-run nominal interest rate is determined by medium-term changes in nominal demand relative to the money supply. By its nature, this policy rule is arbitrary and a highly simplified representation of the policy formation process; there is no reason to think that the parameters and dynamics of the inverted money-demand function, with exogenous money, necessarily describe those of a reasonable rate-setting policy rule.^[3]

In the Murphy Model, the authorities react to a nominal income target. In both macroeconomic models, the primary function of these mechanisms is to ensure that the economy moves towards a stable growth path in the very long run. The Fisher effect is assumed complete and this delivers the real interest rate.

At the other end of the yield curve, determination of the long bond rate is analogous to the macro-models' treatment of the exchange rate. Over the long run, international arbitrage ensures that (typically subject to a constant risk premium) domestic and foreign long-term real interest rates are equalised. In this way, aggregate demand and supply are equilibrated by adjustments in the real exchange rate. Movements in the Australian bond yield away from the foreign rate (equilibrium) are then determined by a term structure calculation.^[4]

2.3 Response to Shocks

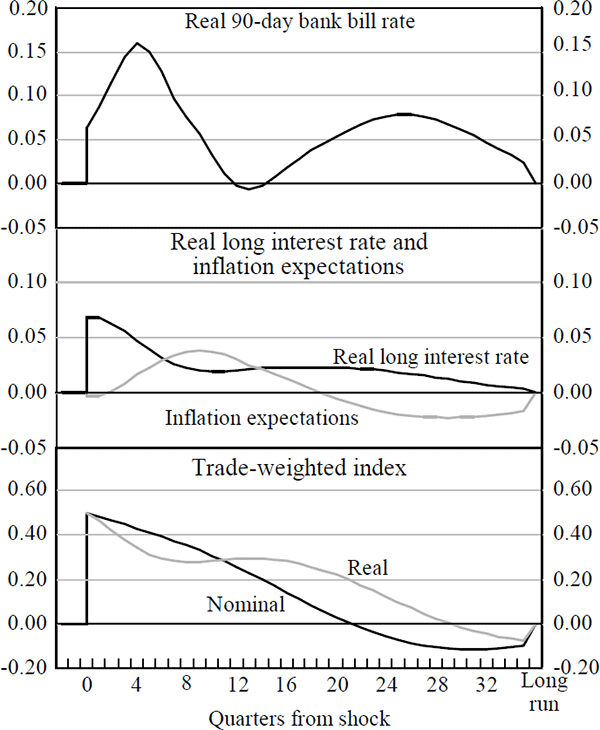
To better illustrate the relevant properties of the macroeconomic models, responses to a domestic monetary policy shock and a terms of trade shock in the TRYM model are illustrated (Figures 1 and 2).^[5]

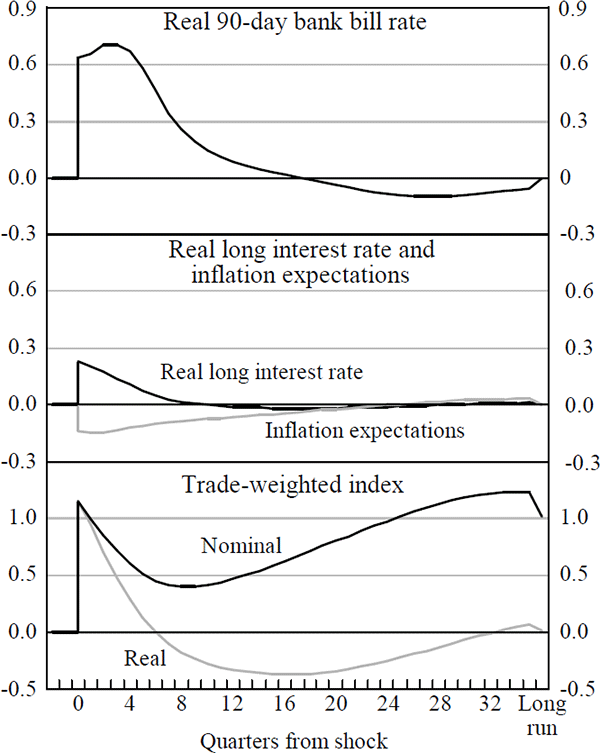
Firstly, a permanent 1 percentage point reduction in the exogenous money supply is effected; this can be thought of as a standard textbook monetary policy tightening. Unfortunately, as described earlier, the macro model is not typically set up to deal with an explicit interest rate shock. Such a simulation in TRYM would involve successive manipulation of the money supply, producing ‘bumpy’ response functions.

In the manner of forward-looking monetary models, the asset price variables ‘jump’ instantaneously in reaction to any shock, typically exhibiting a damped oscillation back to their long-run paths.^[6] A permanent 1 percentage point contraction of the money supply raises real short-term interest rates by 0.63 of a percentage point (Panel 1, Figure 1). This delivers a temporary fall-off in demand and a 1 percentage point reduction in the price level. The price fall is anticipated and agents immediately reduce their inflationary expectations by 0.14 of a percentage point.

The nominal 10-year bond yield jumps up by 0.08 per cent in the initial quarter of the shock; through the uncovered interest parity (UIP) condition, the nominal exchange rate must depreciate by 0.08 of a percentage point per annum for the next 10 years in order to equalise domestic and foreign returns. This requires an immediate appreciation of the exchange rate. Consistent with the imposed theoretical condition of long-run money neutrality, the 1 per cent decrease in the money supply has no effect on real variables in the long run, but leaves the nominal exchange rate appreciated by 1 percentage point.

Alternatively, consider a sustained terms of trade shock, here effected through an increase in the foreign price of exports that is maintained for ten quarters (Figure 2).^[7] This shock raises domestic income. A proportion of the higher domestic income is spent on non-tradeable goods; this places upward pressure on prices and interest rates, appreciating the exchange rate via the UIP condition. The real exchange rate appreciates by around half of a percentage point.

If the shock had been permanent, the macro-model's equilibrium exchange rate would also have appreciated. This is because not all of the higher income arising from a permanent increase in the terms of trade is spent on imports and the current account balance improves; the macro-model's equilibrium exchange rate must then appreciate to generate a smaller trade surplus in the long run and thereby restore external balance.

2.4 Assessment

The textbook-style impulse responses obtained from the macroeconomic models are driven partly by the theoretical assumptions concerning financial market behaviour outlined above. A number of critical points are worth highlighting.

• Within the macroeconomic model framework, the exchange rate and long bond yield display an instantaneous ‘jump’ response to shocks. This is usually followed by a damped oscillation to (partly) unwind the initial impulse. Experience suggests that such impulse responses do not accurately capture real world dynamics.
• Inflationary expectations are also characterised as a ‘jump’ variable; their instantaneous response to shocks occurs before any adjustment in actual inflation. This feature of the macro-model approach does not line up closely with actual experience. In many cases, a change in measured inflationary expectations has not occurred until after a change in actual inflation has occurred.
• Macro models are typically designed to produce policy simulations as responses to shocks under one particular rule – a money-growth rule, for example, in the case of TRYM. By contrast, policy simulations are more naturally examined under alternative policy rules and in terms of changes in the short-term interest rate.
• The size of the estimated exchange rate responses to terms of trade shocks cannot comfortably accommodate the long-standing observed correlation between movements in the terms of trade and the Australian dollar (first documented by Blundell-Wignall and Thomas (1987)).
• The assumption of UIP, embodying risk-neutrality (or a constant risk premium), perfect capital mobility, efficiency in the foreign exchange market, and negligible transactions costs has no empirical support (Smith and Gruen (1989) for Australia; Goodhart (1988) and Hodrick (1987) for international evidence). Quite apart from the validity of the UIP assumption, which turns on the issue of unbiasedness, predictions of future exchange rates based on UIP tend to be highly inaccurate.

With these points in mind, the remainder of this paper proceeds to develop simpler, single-equation behavioural models of the Australian exchange rate and long bond rate. This approach allows characterisation of the distinctive observed behaviour of these variables.

Footnotes

The current (1995) version of the Murphy model consists of 538 equations. TRYM was developed between 1990 and 1993 and consists of 23 estimated equations, 3 financial market identities, 2 default response functions for monetary and fiscal policy and about 100 identities linking these key variables (Downes 1995). [1]

This definition recognises that the current account on external transactions is the counterpart of the capital account. The equilibrium current account represents the desired intertemporal reallocation of resources between countries and identifying the preferred path for the current account means identifying the preferred path for international debt (Clark, Bartolini, Bayoumi and Symansky 1994, p. 14). [2]

As discussed in Edey and Romalis (1996), the exogenous money-growth path target can be compared to a target index for an appropriately weighted average of prices and output. In this way, this approach can be argued to retain some validity for policy analysis, despite the historically poor indicator value of monetary aggregates. However, inverting a money demand function to obtain the short-term interest rate is an invalid statistical process. Edey (1990) presents a general argument that policy under an interest-rate setting rule with freely chosen parameters dominates money targeting apropos the stabilisation of output and prices. [3]

The term structure calculation is macro-model dependent. In the Murphy model, for example, the yield on a 10-year security is set equal to the expected return from holding a continuous sequence of one-quarter securities over the next 10 years; the term premium is assumed to be zero. The expected returns from holding one-quarter securities are model consistent (Murphy 1988). [4]

These results from the Treasury Macroeconomic (TRYM) model should in no way be regarded as being Treasury analyses of the effect of a given policy change or as having the sanction of the Treasury, the Treasurer or the Commonwealth Government. [5]

This long-run adjustment behaviour is largely due to the lagged adjustment processes describing the demand side of the macro models. [6]

The shock is sustained over 10 quarters because this appears to be the average duration of terms of trade shocks historically observed in the data. [7]