RDP 2000-10: Monetary Policy-Making in the Presence of Knightian Uncertainty 5. Implications for Monetary Policy

The two alternative approaches to dealing with Knightian uncertainty presented above have different underlying assumptions about the preferences of policy-makers and the decision rules that they use. In this section we discuss the applicability of these two specifications to the monetary policy decision-making environment.

5.1 Gilboa-Schmeidler Preferences

A decision-maker with Gilboa-Schmeidler preferences is assumed only to care about the probability distribution that delivers the worst case scenario, and chooses the action that minimises the downside of that worst case.

The main application of Gilboa-Schmeidler preferences has been in finance where Knightian uncertainty has been used to explain the behaviour of prices in equilibrium. For example, Epstein and Wang (1994) adapt the static Gilboa-Schmeidler framework to an inter-temporal setting to show that when uncertainty exists in a pure exchange economy, asset prices are indeterminate within some range defined by the degree of uncertainty. Therefore, for a given set of fundamentals, a continuum of prices may exist in equilibrium. The results Epstein and Wang (1994) generate lead them to concur with the view of Keynes (1936) that ‘existing market valuation…cannot be uniquely correct, since our existing knowledge does not provide a sufficient basis for a calculated mathematical expectation’.

Recently, there has been a significant number of applications of robust control methods to the monetary policy decision-making process. This methodology assumes that the decision-maker adjusts policy to minimise the losses associated with the worst-case scenario possible within a prespecified range of outcomes. Therefore, these methods allow for Knightian uncertainty about the model being used and utilise the minimax decision rules implied by Gilboa-Schmeidler preferences. Sargent (1999) and Onatski and Stock (2000) find that when the true model is allowed to deviate from the estimated backward-looking model in very general ways, the result is a policy rule that reacts more strongly to deviations of inflation from target and output from potential than when this uncertainty is not considered. Tetlow and von zur Muehlen (2000) find a similar result using a forward-looking model.

Intuitively, this can arise because the worst-case scenario is the model in which policy has the least ability to affect output and inflation within the range of possible models. In this case, the policy-maker will have to react more to generate the same response, and will therefore deliver a more volatile path of interest rates. Consequently, it can be argued that the assumption that the policy-maker seeks to avoid the worst-case scenario underlies the result that policy is more reactive rather than less under general model uncertainty.

Several authors have also applied robust control methods to cases of model uncertainty that are more specific than the model uncertainty discussed above, but require less assumptions than parameter uncertainty, which assumes a single probability distribution, to obtain similar results. For example, Giannoni (2000) uses a forward-looking model to show that allowing for the effects of such general parameter uncertainty also increases the responsiveness of policy. Onatski and Stock (2000) and Tetlow and von zur Muehlen (2000) show that as the degree of structure placed on uncertainty increases, the responsiveness of the policy-maker decreases.

Robust control methods implement the Gilboa-Schmeidler formulation of the monetary policy decision-maker's problem by using the minimax rule. However, there are several reasons why other methods of incorporating Knightian uncertainty should be explored. First and foremost, the intuition for using a minimax rule in the context of monetary policy does not accord with the way in which monetary policy-makers talk about their decisions. Monetary policy-makers usually talk in terms of the balance of risks rather than in terms of avoiding worst-case scenarios. Second, it is difficult to generalise the results of these models, and to the extent that this is possible, they deliver the result that interest rates will be more volatile in the presence of uncertainty than without it. This runs counter to the original motivation for looking at the effects of uncertainty on monetary policy decision-making.

5.2 Bewley Preferences

Unlike Gilboa-Schmeidler preferences, Bewley preferences assume that the policy-maker cares about the outcomes under all the probability distributions they believe are possible, and do not focus solely on the worst-case scenario. The idea that policy-makers facing Knightian uncertainty cannot make sharp comparisons between some alternatives is intuitively appealing, and accords more closely with the balance-of-risks approach to making monetary policy decisions.

Given the expectations about the ranges of probability distributions that are possible over future periods, it is theoretically possible to establish a range of interest rates that are consistent with these expectations. The inertia assumption implies that the policy-maker should leave interest rates unchanged if the current interest rate lies within this range. One justification for the inertia assumption is that it prevents intransitive, apparently irrational, decisions being made. Given the importance of reputation and credibility for the effectiveness of monetary policy, this would strengthen the appeal of the inertia assumption in the context of monetary policy. Lowe and Ellis (1997) summarise several other arguments for why policy-makers may wish to avoid interest rate moves that have to be reversed, and consequently would prefer to leave interest rates unchanged unless there are sufficient reasons to change them. Some of these alternative arguments for avoiding policy reversals are that they increase financial market volatility and make long-term interest rates less predictable, and therefore weaken the transmission of monetary policy.

The consequence of the inertia assumption is that it is possible for the prevailing level of the nominal interest rate to persist for several periods if the policy-maker believes that the level of the output gap and the real interest rate will remain in similar ranges for several periods. Therefore, the Bewley formulation of Knightian uncertainty has the potential to explain one of the stylised facts of observed interest rates.

If the policy-maker with Bewley preferences has beliefs about the economy that suggest the current stance of monetary policy is no longer within the appropriate range, there will be a discrete shift in the level of the interest rate. Bewley (1986, 1987) does not discuss what the decision rule in this sort of situation should be. Ideally, the policy-maker's decision should be modelled recognising that the decision will affect future decisions, and consequently their expected losses. For example, the policy-maker may wish to choose an interest rate that decreases the amount of uncertainty they are likely to face in the subsequent period. The disadvantage of such a rule in a dynamic setting is that it increases the complexity of solving a problem that is already significantly more complex than the standard decision-making problem under uncertainty. Another alternative is to choose a simple atheoretical rule such as picking the midpoint or boundary of the range.

Figure 5 demonstrates the way in which interest rates would be expected to move if the policy-maker is faced with a given range of interest rates at each point of time. The shaded region is an example of the way in which the range of appropriate interest rates might evolve. In Section 6 we discuss some of the issues that arise for deriving such ranges, but take them as given in Figure 5. At each point in time the policy-maker must decide which interest rate to choose for the next period given their current interest rate and the range of appropriate interest rates for the next period. In Figure 5, the policy-maker does not change the interest rate if the prevailing rate is in the optimal range in the following period and, if the prevailing rate is not in the optimal range, changes the interest rate to the midpoint of the range.

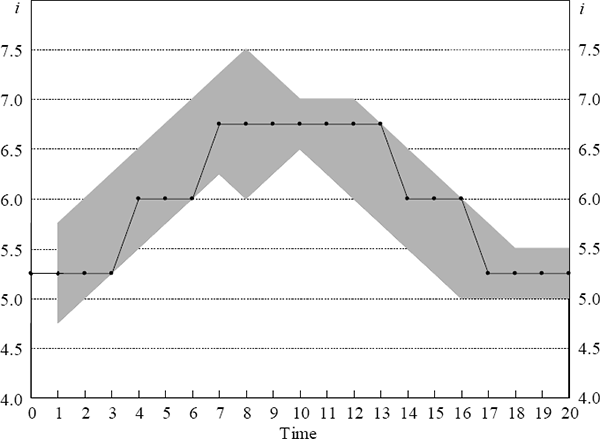
Figure 5 exhibits step movements in interest rates, and the way in which the bands of appropriate interest rates are assumed to evolve delivers sequences of interest rate movements in the same direction. Another feature of this framework is that interest rates are less likely to change as the range of possible optimal interest rates increases, which will occur if uncertainty increases.