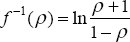RDP 2001-05: Understanding OECD Output Correlations Appendix A: The Transformation of the Dependent Variable

The dependent variable, the sample correlation of GDP growth, must lie between −1 and 1. However this implies that the error term in Equation (1) cannot be normally distributed. This issue has not been addressed in previous papers using these types of models (Frankel and Rose 1998; Imbs 2000), presumably under the assumption that the variance of the error term is sufficiently small; however, our results suggest that the variance of the error term is not very small and it is necessary to take account of this restriction.

To do so, we assume that there is a function f(·) that transforms the linear regression model so that it satisfies this constraint. That is, we rewrite the model as:

Here, ρ_ij,τ is the correlation measure for countries i and j for time period τ, W_ij,τ is a set of regressors of the general model, and ε_ij,τ is the error term. The function f (·) must map from the real line to the interval −1 to 1; we use the following function:

As w gets very large (small), f (w) gets closer to 1 (−1); and f (0) = 0. To estimate the model, we transform the LHS variable of Equation (4) by the inverse of f (w) :

To recover the predicted correlation values from the model, we apply the function f (w) to the predicted values of the estimated model.