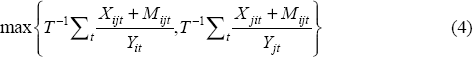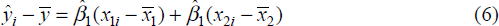RDP 2001-05: Understanding OECD Output Correlations 3. Empirical Results
September 2001
- Download the Paper 227KB
3.1 Transmission Channels
We begin by examining individually the three different classes of transmission mechanisms identified previously: trade in goods and services; trade in assets; and policy influences. We estimate a simple linear regression model for each channel, in each case considering a number of different possible measures. The results from using OLS are reported in Table 2 and, based upon the discussion above, those from using instrumental variables (IV) in Table 3.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Constant | 1.2028 (6.1601) |
1.2903 (5.9633) |
1.2597 (5.5139) |
1.1637 (9.0635) |
1.0020 (7.6992) |
1.6832 (3.1647) |
0.8559 (5.9340) |
−0.3048 (−1.1610) |
| Trade in goods | ||||||||
| Trade intensity: total | 0.1490 (3.4136) |
|||||||
| Trade intensity: exports | 0.1433 (3.4872) |
|||||||
| Trade intensity: imports | 0.1402 (3.1030) |
|||||||
| Trade in assets | ||||||||
| FDI intensity | 0.1126 (4.8911) |
|||||||
| Interest rate spreads: long | −0.5670 (−3.5630) |
|||||||
| Share return spreads | −0.3459 (−2.0765) |
|||||||
| Monetary policy | ||||||||
| Interest rate spreads: short | −0.3250 (−1.9615) |
|||||||
| Exchange rate deviations | −0.2686 (−3.3285) |
|||||||
| R-bar squared | 0.093 | 0.100 | 0.078 | 0.152 | 0.086 | 0.028 | 0.017 | 0.066 |
| Correlation | 0.284 | 0.297 | 0.261 | 0.389 | 0.296 | 0.166 | 0.150 | 0.250 |
| Sigma | 0.554 | 0.552 | 0.559 | 0.536 | 0.556 | 0.573 | 0.576 | 0.562 |
|
Notes: The countries used are the 17 OECD countries identified in the text, providing 136 country pairs (the number of observations for the regression models). The dependent variable is a transformation of the bilateral GDP growth correlations calculated over 1980–2000. See Appendix A for details of the transformation. Numbers in parentheses are White heteroskedasticity robust standard errors calculated using the HC (3) adjustment as described in Davidson and MacKinnon (DM) (1993, p 554). Correlation refers to the simple correlation between the actual and predicted correlations (not the transformed correlations) of the model. Sigma is the standard error of the residuals. |
||||||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| Constant | 1.6179 (6.9771) |
1.7540 (6.8900) |
1.7965 (6.3477) |
1.4532 (7.2469) |
1.2457 (6.3887) |
3.9005 (4.3836) |
1.4322 (7.2820) |
−0.5736 (−1.7511) |
| Trade in goods | ||||||||
| Trade intensity: total | 0.2503 (4.5218) |
|||||||
| Trade intensity: exports | 0.2386 (4.6567) |
|||||||
| Trade intensity: imports | 0.2530 (4.3097) |
|||||||
| Trade in assets | ||||||||
| FDI intensity | 0.1696 (4.4574) |
|||||||
| Interest rate spreads: long | −0.9048 (−3.5296) |
|||||||
| Share return spreads | −1.0492 (−3.7002) |
|||||||
| Monetary policy | ||||||||
| Interest rate spreads: short | −1.0369 (−4.3779) |
|||||||
| Exchange rate deviations | −0.3491 (−3.4973) |
|||||||
| OI restrictions | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Instrument quality | 0.610 | 0.606 | 0.569 | 0.487 | 0.288 | 0.328 | 0.335 | 0.621 |
| DWH | 0.001 | 0.001 | 0.001 | 0.019 | 0.132 | 0.001 | 0.002 | 0.126 |
| Correlation | 0.280 | 0.294 | 0.258 | 0.388 | 0.296 | 0.156 | 0.143 | 0.250 |
| Sigma | 0.564 | 0.562 | 0.571 | 0.544 | 0.562 | 0.612 | 0.606 | 0.560 |
|
Notes: As for Table 2. The numbers in parentheses are t-statistics computed using White heteroskedasticity-robust standard errors for IV calculated using HC (3); see DM (1993, p 609). OI refers to the marginal significance levels for the test of the over-identification restrictions; see DM (1993, p 235). DWH refers to the marginal significance level from a Durbin-Wu-Hausman test for consistency of the OLS estimate; see DM (1993, p 239). The instrument quality measure is the R-bar squared from the first stage regression. |
||||||||
3.1.1 Trade in goods and services
The principal traditional channel for spillover effects is trade, with the sharpest spillovers [from the United States] to those countries with the highest ratios of exports to the United States relative to their incomes. (Meyer 2001)
Trade in goods and services is the most commonly identified mechanism by which fluctuations in the level of activity in one economy spill over into other economies. An expansion in aggregate demand in one country may be transmitted through an increase in demand for traded goods and services to other countries. The extent to which this happens and contributes to the correlation of output growth between two economies depends upon two factors: the extent of bilateral trade and its importance in aggregate demand. One can also motivate a supply-side explanation through intermediate imported inputs. If growth in one economy is associated with an expansion in production of intermediate inputs used by a second economy then, through falling prices or simply greater access to supply, production in the second economy may also rise, causing output growth to be correlated.[10] Both of these explanations point toward a positive relationship between bilateral trade and output growth correlations.
The possibility exists, however, that increased trade between two countries may lead to greater specialisation to capture gains from comparative advantage. If industry specific shocks are important, then we might expect less correlation between two countries as each is affected by idiosyncratic shocks.[11] This suggests that in theory at least the role of bilateral trade in explaining cross-country growth correlations is ambiguous.
To examine the role empirically we require a measure of aggregate bilateral trade intensity between pairs of countries. There are a number of indices that one might use, all of which are somewhat arbitrary. We use the natural logarithm of the following index,
where Xijt is total nominal merchandise exports from country i to country j in period t, Mijt is total nominal merchandise imports of country i from country j in period t, and Yit is nominal GDP for country i in period t. In principle, the two numerators in the above index should be equal, however differences can arise since Xijt and Mjit are measured by different statistical agencies. See the data appendix for further discussion.
Our index captures two aspects of bilateral trade. First, the numerator measures the amount or intensity of trade between two countries by summing bilateral imports and exports. Second, by scaling with nominal GDP we can measure the relative importance of the bilateral trade to total production in each economy. We use the maximum of the average over the sample of the two possible measures because what is likely to matter for the interdependence of two economies is whether or not at least one is exposed to the other. As a specific example, consider Australia and Japan. Trade with Japan is large for Australia and will be, relative to other Australian trading partners, a large share of Australian GDP. From a trade perspective, this suggests that Australia is well integrated with Japan. From Japan's perspective, the share of bilateral trade with Australia relative to Japanese GDP is small, principally because Japan's GDP is large and Japan has other more important trading partners. So, arguably, the interdependence with Japan is largely one way and we would expect shocks to flow one way – from Japan toward Australia. But this may be sufficient for the two countries to have a correlated growth rate. Using the maximum of the two trade intensities captures this possibility of one-way interdependence without sacrificing information about possible two-way interdependence.[12]
In addition to using Equation (4) as an index of total bilateral trade, we also calculate analogous measures for imports and exports individually. This allows us to examine whether exports or imports appear to be a more important transmission channel.
The results for the three measures of trade intensity are reported in columns (1)–(3) in Table 2 (OLS) and Table 3 (Instrumental Variables). Setting aside any concerns about endogeneity for the moment, consider first the OLS estimates in Table 2. For all three measures of trade intensity we find a statistically significant positive effect on bilateral output correlations. The fit of these regressions is also similar; the R-bar squared ranging from 8 to 10 per cent. So that we can compare these results to the IV results, we also report the simple correlation between the predicted and actual correlations; consistent with the low R-bar squared values, these are just below 0.30.
A word of caution about interpreting the regression coefficients is necessary at this point. The dependent variable in the regression model is a non-linear transformation of the bilateral correlations we are modelling. It is necessary to use this transformation to ensure that the predicted values of the model lie between −1 and 1 consistent with correlation measures; we discuss the transformation we use in greater detail in Appendix A. As a result of the transformation, it is not straightforward to put a meaningful interpretation on the size of the coefficient estimates reported in the tables and for the time being we focus purely on their sign and significance. At a later stage, when we have a richer representation of the data, we provide a quantitative interpretation of the results.
There are a number of points that emerge from these results. First, although trade is a statistically significant explanation of the bilateral output growth correlations, it does not explain very much. Second, the positive relationship between trade and output growth correlations suggests that it is the transmission of shocks through trade that explains the correlation. That is, there is no evidence to support the conjecture that greater trade through specialisation leads to less synchronised economies. This positive relationship is consistent with other studies, Canova and Dellas (1993); Frankel and Rose (1998) and Clark and van Wincoop (1999). Finally, there is some (very) weak evidence that export linkages matter slightly more; the export measure provides a marginally better fit but the difference is small.[13]
The instrumental variables results are reported in Table 3 and provide the same conclusions.[14] Interestingly, the coefficients on trade are much larger than the OLS estimates reported in Table 2; exactly why this is so is not clear. As we develop the model further, however, this issue goes away and so need not concern us here.[15] The difference in the OLS and IV estimates is reflected in the Durbin-Wu-Hausman (DWH) tests (Davidson and MacKinnon 1993), the marginal significance levels for which are reported in the table. These indicate that we can reject the hypothesis that the IV and the OLS estimates are the same, providing support for using IV methods. Also reported in Table 3 for each regression are measures of instrument quality; for these single variable models, we report the R-bar squared from the first stage regression. A larger number indicates that the instruments we have are good in the sense that they explain the endogenous regressors well.
Finally, Table 3 reports tests for the over-identifying restrictions, as described in Davidson and MacKinnon (1993). For all three models, and indeed all of the models in Table 3, we reject these restrictions. The most likely explanation is that the channel we are modelling, in this case trade, is not the only means by which our instruments influence the bilateral correlations. It may be the case that our instruments explain other channels, for example trade in assets or common monetary policies, and our model is incorrectly restricting their role to operate only through trade. It may also be the case that our instruments explain output correlations directly themselves. We return to these issues below when we develop a more complete empirical model.
3.1.2 Financial linkages
…additional linkages most likely arise directly and indirectly, at least in part, from the increasingly tight connection among financial markets and the resulting synchronization of the global equity correction. (Meyer 2001)
Financial market linkages are a widely acknowledged mechanism for the international transmission of business cycle shocks. To examine this transmission channel, we consider three different classes of investment; foreign direct investment (FDI), trade in equities, and trade in long-term bonds. For FDI, we can obtain information on stocks and flows on a bilateral basis so that we can construct bilateral indices in much the same way as we do with trade flows. For equity and debt instruments, it is difficult to construct meaningful measures of bilateral flows so we measure integration in this context using bilateral spreads in asset returns.
The transmission of shocks through debt and equity markets is relatively straightforward to motivate. Suppose that capital is relatively mobile between two economies, then a change in saving and investment decisions in one is likely to affect the price and availability of financial assets in the other, which should, all else equal, lead to more closely synchronised business cycles. FDI is less straightforward to motivate as a transmission channel so we need to consider this in slightly more detail.
We can think of a number of ways in which the extent of foreign direct investment can be related to the degree of business cycle correlation. At a simple level we can think in terms of aggregate demand and supply effects in much the same way as we view trade intensities. That is, countries that are closely integrated through FDI may transmit shocks to each other through the changes in FDI positions brought about by idiosyncratic shocks. In this case, it is FDI flows that matter. Our view, however, is that this is not a particularly important channel, largely because the size of these flows (on average) relative to GDP are likely to be small nor do we anticipate that these flows will be very cyclical, certainly not to the same extent as trade flows.
It seems more useful instead to think in terms of FDI stocks and how strong bilateral FDI positions might contribute to the synchronisation of business cycles. There are a number of possibilities. First, multinational firms may distribute the effects of local macroeconomic shocks throughout the organisation thus distributing the shock, to some extent, from one economy to another. An example of this might be the retrenchment of staff worldwide in a multinational organisation suffering a downturn in some of its markets. Similarly, if FDI is generated by multinationals sourcing production of intermediate inputs abroad, then the effects of changes in demand for final products may be transmitted to countries providing the intermediate inputs. From a similar perspective, income flows generated by FDI positions may also serve to synchronise the business cycles of countries with strong FDI linkages (Meyer 2001). Finally, FDI may also serve as a means by which technology and ideas are transferred between countries, which may also contribute to the correlation of output growth.[16]
To measure bilateral direct foreign investment intensity, we use an index identical in structure to that used for bilateral trade, with inward and outward foreign direct investment positions in place of exports and imports. To measure financial integration of equity and debt markets on a bilateral basis, we construct spreads on real returns for both markets. We then calculate the standard deviation of these spreads over the sample period. The greater the extent of financial integration between two countries, the lower this measure should be; that is, there should be a negative relationship between this measure and the correlation of output growth.[17]
We consider each measure individually; these results are reported in columns (4)–(6) in Table 2 and 3. As before, the OLS and IV results provide the same information. Now, however, it is very difficult to justify the use of OLS, particularly with respect to the spreads on the real bond and equity returns, as the direction of causation is clearly ambiguous. Countries with highly correlated business cycles, say due to common shocks, are likely to have similar patterns of interest rates and equity returns even if there is no financial linkages between the two economies. Our IV estimates attempt to control for this. They use exogenous information to predict the extent of variation in real returns between two countries; we then consider the relationship between the predicted variation in real returns and the correlation in output growth. In principle, this provides a consistent estimate of the true effect of the relationship between financial integration and output growth correlations.[18]
For both the OLS and IV results, the coefficients on the three measures of financial integration, FDI intensity, Interest rate spreads: long, and Share return spreads, are statistically significant and of the predicted sign. In terms of overall fit, either the R-bar squared measure for the OLS results or the simple correlation between the predicted and actual output correlations, the best model is that for intensity of FDI. The weakest fit comes from the spread on real equity returns, in large part reflecting the high degree of variation across country pairs for this variable. Despite the weakness of the fit, the finding that equity market linkages are significant is consistent with a number of studies that have emphasised this channel; Meyer (2001) points to this as a possibly important aspect of the current global situation. For Australia, both de Roos and Russell (1996) and Dungey and Pagan (2000) find evidence in time series data that US asset price shocks have an important impact on Australian activity. Our results suggest that this finding for the US and Australia is consistent with the results for a much larger group of OECD countries.
3.1.3 Monetary policy
The similarity or otherwise of monetary policies of two countries is often put forward as a principal explanation for common business cycles. For example, differences in monetary policies are a likely explanation for the lower than expected correlation between the UK and other European countries in the European Exchange Rate Mechanism (ERM) (Kohler 2001). Similarly, the high correlation of output among members of the ERM is likely to be due in part to the consequent common monetary policy (see the discussion in Frankel and Rose (1998)).
Observed common behaviour of monetary policies between two (or more) countries is likely to reflect one of three factors: similar responses to common shocks; similar responses to shocks that are transmitted from another country or the coordination (explicitly or implicitly) of monetary policy. Under a flexible bilateral exchange rate regime, common monetary policies (for example, highly correlated short-term interest rates) can arise from common underlying shocks. The correlation of interest rates will strengthen the more similar the two economies are in structure, including the mandate and strategies of the central banks involved (Meyer 2001). In this case, common monetary policies and business cycle behaviour are an indication of common economic structure and underlying shocks.
This is not the only explanation, however, for commonality of both business cycles and monetary policy. If two countries are closely integrated through trade and financial markets, then an idiosyncratic shock to one can be transferred to the other through these linkages; if the two countries share similar monetary policy objectives, then we again observe common business cycle and monetary policy behaviour, although this time the underlying explanation is the presence of other transmission channels. An important implicit assumption in this argument is that the flexible exchange rate does not insulate the small country from all types of external shocks.[19]
With fixed bilateral exchange rates, the monetary policies of two countries are explicitly and automatically coordinated. In this case, monetary policy serves as a transmission channel for idiosyncratic shocks and also ensures a common response to common shocks; in both instances, the coordinated monetary policy is likely to contribute to stronger correlation of growth cycles.
Based upon all of these arguments, we expect a positive relationship between the closeness of monetary policy stance and similarity of business cycles for any two countries. Clearly, however, what underlies the relationship and the direction of causation is very difficult to discern. Empirically, we need to control for the endogeneity of the behaviour of monetary policy as well as for other aspects that might explain the common growth cycles (e.g. trade and financial integration).
For the moment, our principle concern is examining the simple relationship between monetary policy stance and business cycle correlations, so we abstract from other influences (as we have done in the previous sections). We consider two measures of the degree of coordination between two economies. The first is a measure of the volatility of the bilateral real short-term interest rate differentials; the lower this volatility, the more similar is monetary policy in two countries.[20] The second is the volatility of the bilateral nominal exchange rate, which is more directly related to whether or not two countries explicitly or implicitly maintain a fixed exchange rate.[21]
Columns (7)–(8) of Tables 2 and 3 contain the results for our measures of the degree of monetary policy coordination. As before, the OLS and IV results provide the same information: both measures are statistically significant and of the correct sign. Greater volatility of either the short-term interest rate differentials or the bilateral exchange rates are associated with lower output growth correlations. Based upon the R-bar squared for the OLS estimates and the correlation of actual and predicted values for both the IV and OLS estimates, the exchange rate volatility measure provides a better fit of the data.
The estimates in column (8) have a rather interesting prediction. Suppose that two countries can fix their nominal exchange rate, then over time they should expect to see an increase in the correlation of their growth rates. To be specific, consider the case of West Germany and Austria, the pair of countries with the minimum amount of bilateral exchange rate volatility in our sample.[22] Based on model (8) in Table 3, the exchange rate volatility for these two countries predicts a bilateral correlation of 0.69 (the observed bilateral growth correlation for this country pair is 0.61). We have to be somewhat careful, however, in attributing this to transmission of shocks through the common monetary policy arising from fixed exchange rates; it may reflect (at least in part) the indirect effect of lower exchange rate volatility on bilateral trade flows.[23] In order to control for this, we need to consider more general models.
The results overall in Tables 2 and 3 are interesting for a number of reasons. First, we are able to confirm the findings by Frankel and Rose (1998) of the role of trade in goods in explaining the bilateral output growth correlations. It is also clear, however, that trade is by no means the full explanation. The OLS results indicate that bilateral trade intensity can explain about 10 per cent of the cross-country variation in bilateral growth correlations. What is also apparent is that we can find a number of other variables in addition to trade in goods that seem to provide channels for the transmission of shocks between countries. In fact none of the variables that we consider clearly dominates in its ability to explain bilateral growth correlations.
How good are these models? Not surprisingly our results also indicate that none of the single variable models does a particularly good job at explaining bilateral correlations. For the OLS results, we obtain R-bar squared statistics ranging from 0.02 to 0.15. A more serious concern arises with the instrumental variables results, though. For all of the models, the over-identifying restrictions are strongly rejected, indicating some form of model misspecification. The most reasonable interpretation of these results is that important explanatory factors are omitted from these regressions, an issue we now consider.
3.2 Industry Structure and Transmission Channels
We now extend the models of the previous section to control for the effects of common shocks. To do this, we follow Imbs (2000) and use a measure of the difference or distance between the industry structures of two economies. Imbs argues that if sector-specific economic shocks are a major source of economic fluctuations then countries with similar economic structures should display relatively high bilateral output growth correlations. To measure the distance between the industry structures of two countries, we construct the following index based upon Krugman (1991):
where lik,t denotes employment in sector k as a share of total employment in country i and M is the total number of sectors. (See Appendix B for further details.) For our analysis, we use the employment shares for 1989, roughly the middle of the sample.
Table 4 presents estimates of models containing the industry structure index and our various transmission channels. Initially, we considered two measures of cross-country differences in industry structure: one (similar to Imbs) using three-digit employment data for manufacturing and a second broader measure using one-digit employment data for the entire economy. Given the manufacturing industry's declining relative importance in OECD economies and the broader nature of the one-digit index, the latter measure would seem in some ways to be a preferable indicator of cross-country differences in industry structure. It turns out that this is indeed the case; the manufacturing-based index performs substantially worse than the broader industry measure. Consequently, we only reports results for the broader index.[24]
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| Constant | 1.0551 (5.7027) |
1.7915 (7.1425) |
1.6260 (7.1621) |
1.6469 (6.2788) |
3.8761 (4.6442) |
1.7780 (6.5806) |
−0.0741 (−0.1897) |
| Industry structure | |||||||
| Total industry | −1.9889 (−2.6183) |
−1.1397 (−1.5324) |
−1.1088 (−1.5463) |
−1.8987 (−2.4935) |
−1.5034 (−2.0741) |
−1.7900 (−2.1567) |
−1.7134 (−2.2317) |
| Trade in goods | |||||||
| Trade intensity: total | 0.2280 (4.0765) |
||||||
| Trade in assets | |||||||
| FDI Intensity | 0.1529 (4.1322) |
||||||
| Interest rate spreads: long | −0.8490 (−3.4638) |
||||||
| Share return spreads | −0.9306 (−3.5081) |
||||||
| Monetary policy | |||||||
| Interest rate spreads: short | −0.9499 (−4.2693) |
||||||
| Exchange rate deviations | −0.3188 (−3.2285) |
||||||
| OI restrictions | – | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Instrument quality | – | 0.607 | 0.484 | 0.284 | 0.324 | 0.331 | 0.618 |
| DWH | – | 0.002 | 0.045 | 0.167 | 0.002 | 0.003 | 0.203 |
| R-bar squared | 0.052 | – | – | – | – | – | – |
| Correlation | 0.241 | 0.317 | 0.415 | 0.369 | 0.220 | 0.232 | 0.330 |
| Sigma | 0.566 | 0.552 | 0.532 | 0.542 | 0.588 | 0.585 | 0.545 |
|
Notes: As for Table 3. Estimates are by instrumental variables except for column (1) which is by ordinary least squares. |
|||||||
For all of the models in Table 4, which consider the different transmission channels discussed previously as well as the industry structure index, we find a statistically significant role for differences in industry structure as an explanation of bilateral growth correlations. The greater the difference in industry structures of a pair of countries, the lower is their correlation in their output growth.
When considered by itself, it explains about 5 per cent of the cross-country variation.[25] When included with the other transmission channels it remains statistically significant and the correct sign. Interestingly, it does not significantly alter the contributions of each channel; the coefficient estimates for these variables are slightly smaller (in absolute value) than in Table 3 but the same order of magnitude.
One attractive aspect of the models in Table 4 is that they contain variables that can capture both the transmission of country-specific shocks between countries and also the impact of common shocks within countries. This goes some way to addressing concerns that the transmission channels such as the short-term interest rate and exchange rate deviations are capturing the effects of common shocks, explaining both common monetary policy and common business cycles. It is clear, however, from the test of the over-identifying restrictions for the various models that all of the important factors in explaining bilateral growth correlations have not yet been included.
3.3 A Dominant Transmission Channel?
The results in Tables 3 and 4 suggest that there are a number of channels, other than trade in goods, by which shocks can be transmitted between countries. In Table 5 we examine the effect of augmenting a baseline model – containing the industry structure variable and bilateral (goods) trade intensity – with the other possible channels identified in Tables 2 and 3. To minimize problems of co-linearity, we begin by augmenting the baseline equation with each alternative transmission channel sequentially.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
|---|---|---|---|---|---|---|---|
| Constant | 1.7398 (6.8711) |
1.7522 (7.0644) |
3.1018 (4.2377) |
1.8493 (8.1527) |
1.6796 (2.4648) |
2.8733 (3.8689) |
2.4648 (3.0859) |
| Industry structure | |||||||
| Total industry | −1.0706 (−1.4820) |
−1.0582 (−1.3937) |
−1.0679 (−1.4474) |
−1.1832 (−1.5639) |
−1.1482 (−1.5333) |
−1.1414 (−1.5222) |
−1.1053 (−1.4872) |
| Trade in goods | |||||||
| Trade intensity: total | 0.1094 (1.0548) |
0.2551 (3.0417) |
0.1795 (2.9520) |
0.2071 (2.6751) |
0.2201 (2.9112) |
0.1645 (2.6632) |
0.1091 (1.6163) |
| Trade in assets | |||||||
| FDI intensity | 0.0887 (1.3387) |
||||||
| Interest rate spreads: long | 0.1817 (0.5173) |
||||||
| Share return spreads | −0.4839 (−1.9049) |
−0.3815 (−1.5311) |
−0.5829 (−2.4827) |
||||
| Monetary policy | |||||||
| Interest rate spreads: short | −0.1648 (−0.6502) |
−0.1716 (−0.7611) |
|||||
| Exchange rate deviations | −0.0243 (−0.1864) |
−0.2003 (−1.5921) |
|||||
| OI restrictions | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Instrument quality | 0.194 0.184 |
0.080 0.068 |
0.531 0.546 |
0.162 0.152 |
0.712 0.728 |
0.469 0.589 0.209 |
0.336 0.227 0.270 |
| DWH | 0.006 | 0.084 | 0.338 | 0.934 | 0.183 | 0.397 | 0.231 |
| Correlation | 0.392 | 0.271 | 0.317 | 0.327 | 0.322 | 0.329 | 0.345 |
| Sigma | 0.534 | 0.573 | 0.556 | 0.548 | 0.550 | 0.549 | 0.546 |
|
Notes: As for Table 4. An instrument quality measure due to Shea (1997) is reported for each endogenous variable. Model (6) uses a different set of instruments than those used in models (1)–(5); see text for details. |
|||||||
It is apparent from columns (1) to (5) that trade in goods tends to dominate the other potential transmission channels in terms of statistical significance. The main exception is the model including goods trade and FDI reported in column (1), in which FDI has a larger t-statistic than trade intensity, although neither variable is individually significant by conventional criteria. The low individual t-statistics are likely a reflection of the high correlation (0.75) between our measure of FDI and total trade intensity. Rather than try and include both variables in the subsequent models we focus on trade intensity rather than FDI. On balance we feel that trade intensity is better understood as a transmission mechanism than FDI and in addition the degree of measurement error is likely to be greater in the FDI data than in the trade data. However as a check on the validity of this choice, we ensure that our final results are not significantly affected by the use of trade intensity rather than FDI intensity.
Of the remaining transmission channels only the volatility of equity return spreads maintains its significance in the presence of trade intensity. Column (3), which includes industry structure, trade intensity and the spread on real equity returns provides two significant transmission channels, trade in goods and trade in financial assets, as well as controlling for common shocks. It seems natural to consider augmenting this model with the remaining transmission channel, monetary policy. This is done in column (6) using short-term interest rate spreads and column (7) using exchange rate volatilities. Comparing the two models, exchange rates appear to be more important than short-term interest rates in the transmission of shocks between countries. The lack of statistical significance of the volatility of short-term interest rate spreads provides some direct evidence against the hypothesis that coordination of monetary policy is an important transmission mechanism for shocks. The results in column (7) point to a model that has three transmission channels as well as the industry structure index controlling for common shocks. This suggests that share markets and exchange rate arrangements, along with trade intensities, are important transmission channels in their own right.
Although the model in column (7) appears to capture quite well the three transmission channels we initially posited as important as well as controlling for common shocks to some extent, as a statistical model it cannot be viewed as complete. The test for the over-identification restrictions of the model is still rejected, indicating that the model is still not correctly specified. As we discussed previously, we suspect that the variables we are using as instruments to model the transmission channels, or at least some of them, are important for explaining the variation in output growth correlations. In addition, we suspect that there are other characteristics that may help to explain cross-country growth correlations.
3.4 A General Model
We now examine in more detail whether there are certain characteristics that if shared by two countries make it more likely that their growth rates will be correlated. Such common characteristics might make it easier for shocks to be transmitted between countries or simply make a pair of countries more susceptible to a particular type of common shock. The set of country characteristics that we consider include: common legal origins, accounting standards, the extent of structural economic reform, and a measure of the speed to adoption of information and communications technology (ICT). We consider the potential role of each of these variables in turn and then consider the empirical results.
Origin of legal system
The basis for trade in goods and financial assets is the existence and enforcement of property rights enforced through a country's legal system. In a recent paper, La Porta et al (1998) argue that legal systems can differ quite markedly across countries in terms of the degree of legal protection given to agents engaged in commercial activity – particularly investment. The authors classify the legal systems of various countries into four categories – English, French, German and Scandinavian – based on the origin of the country's legal system and laws. For example, in our sample of OECD countries, the US, UK, Canada, Australia and New Zealand are classed as having legal systems that evolved from the English common-law tradition.
We make two conjectures with respect to the legal origin variable. First, we suspect that countries with similar legal systems may have more integrated financial markets and institutions, over and above what is captured by the transmission channels previously considered. Thus, even controlling for these channels, parings of countries with similar legal origins will tend to more correlated business cycles. Second, legal systems may underlie different economic structures; as a consequence, we may observe different effects of common shocks, both the initial response as well as the propagation of these shocks, in countries with different legal systems. La Porta et al emphasise that different legal structures give rise to differences in corporate governance, particularly with respect to investor protection. They point to further research that suggests the quality of investor protection is related to the size of debt and equity markets, which we suspect may be important for the advent or propagation of financial sector shocks. Similarly, different legal structures may give rise to or be closely correlated with different forms of labour market organisation, something that may also underlie the advent or propagation of macroeconomic shocks.
To pursue these ideas, we use data from La Porta et al to construct a set of dummy variables based upon country of legal origin. The most general is defined as 1 if a country pair shares a common legal origin and 0 otherwise. We also construct more specific pairings, for example 1 if both share Scandinavian legal origin and 0 otherwise. We do this for each of the four possible origins.
Accounting standards
La Porta et al put accounting standards forward as an important aspect of corporate governance relating to investor protection, so for similar reasons discussed with respect to the country of legal origin variables, we also construct a bilateral index of accounting standards. We can also motivate the use of this variable as capturing the ability of countries to engage in international trade, in goods or financial assets. We conjecture that the higher the quality of accounting standards – capturing both the sophistication and transparency of accounting practices – the less costly it is for firms to engage in trade and investment overseas.
La Porta et al present an index of the quality of accounting standards for a wide range of countries, including those we use in this study. We construct a bilateral index by taken the natural logarithm of the product of the two countries' indices. The construction of the index in this way is relates to the second of the two motivations; that is, country pairs with a high index are more likely to be engaged in international transactions.[26] We conjecture that the larger this bilateral index for any two countries, the more likely are their business cycles to be correlated.
Index of structural economic reform
A virus reached Australia in the early 1980s. It travelled from Britain to the USA and then to Australia. Anglo-Saxon societies appeared to be particularly prone to its impact, and in the South Pacific, New Zealand and Australia offered themselves as willing victims. The virus has a name: economic rationalism. (Daly 1993)
Over the past twenty years, a number of countries in our sample have made considerable efforts to deregulate their economy, including the English-speaking economies identified by Daly (1993). Other countries, for example Italy, have undertaken much less deregulation. As well as leading to a convergence in the degree of the flexibility of economies, so that the effects of common shocks are likely to be similar, this process of deregulation may itself be a type of common shock to these economies.
We construct a measure of the bilateral differences in the amount of structural economic reform between countries using a country index constructed by Lehmann Brothers and reported in The Economist (2001). On the basis of a large number of indicators, it rates countries on a scale of 0 to 10 on their structural economic policies (0, worst; 10, best). We use the distance between reforms in this instance because it serves best to capture the arguments above. Two countries that have pursued reforms are conjectured to be more likely to respond similarly to common shocks. For example, if we think that structural reforms have made countries more flexible, then they are likely to respond more quickly to external shocks. Alternatively, if we think of these reforms as a source of shocks, then the index we construct in some sense captures the similarity of the shocks that any two countries have faced. In both of these cases, we expect a negative relationship between the distance between reform policies and the correlation of the business cycles.
Openness to new technology
It was only in the 1990's that diffusion of the Internet and the WWW, accelerated falls in ICT prices and the emergence of user-friendly computer software allowed technologies to interact on an unprecedented scale, and allowed ordinary people and small businesses to use them productively.
If a new industrial revolution really has begun, it will survive any cyclical collapse in the US economy. And with Australia one of the world's top investors in IC technology, the revolution should soon spread down under. If it does, we're in for a fast but rocky ride. (Gittins 2001)
The development and use of new technology is one potential source of business cycle fluctuations. From a supply side perspective, new technologies can contribute to better means of production, generating an expansion in investment, employment, and output. New technologies may also be an important source of cyclical behaviour through their effects on financial markets. Fisher (1933) in his discussion of the stock market boom leading up to 1929 identifies inventions and new technologies as principal underlying forces. Similar arguments can be applied to the technology driven stock market bubble of the late 1990s.
To investigate this, we construct a measure of the speed with which the economies in our sample adopted recent innovations in ICT, namely mobile phones, personal computers and the Internet. Essentially, we look at the degree of penetration of these technologies for each country in our sample around 1995–1996.
This measure can in principle capture two possible contributions to the behaviour of economic growth. The first is the actual impact of ICT on productivity and output growth in those countries that were early adopters of these technologies. The influence of this on bilateral growth correlations, however, will be restricted to the 1990s at best. Alternatively, and this is what we hope to capture, this measure serves as a proxy for the general willingness (or ability) of countries to adopt new technologies per se. For reasons similar to those discussed for the structural economic reform index, we construct the bilateral index as a distance measure and we again anticipate that the measure will be inversely related to the correlation of output growth.[27]
Results
In Table 5 we found evidence that suggested integration of stock markets and coordination of monetary policy were channels – additional to trade in goods – by which shocks could be transmitted between countries. To conclude our empirical work we report results obtained from augmenting the model in column (7) in Table 5 with the various characteristics. In addition to the characteristics discussed above we also include a dummy variable for adjacency of countries and an index of common language (see Frankel and Rose (1998)). So far we have used these variables as instruments, however, we now include them directly in the structural model. A common language may promote economic integration by influencing the level of communication and flow of ideas between countries, while adjacency may pick-up common historical ties between particular countries.[28]
Results from estimating the most general model are reported in Table 6. In column (1) we include all the characteristics and use the aggregate dummy variable for country of legal origin. It is apparent that a number of the variables in the general model are not significant, including: trade intensity; equity returns; industry structure; legal origin; structural reform and adjacency. If we retain trade intensity in the model but delete the other insignificant variables we obtain the results in column (2). This model suggests that in addition to the trade and exchange rate channels, three characteristics are important in explaining output correlations: good accounting standards; common take-up of new technology and a common language. In fact the common language variable and the common legal origin variable seem to contain similar information. This can be seen from the results in column (3) where common language is replaced by common legal origin, with very little effect on the results.
| (1) | (2) | (3) | (4) | (5) | |
|---|---|---|---|---|---|
| Constant | −12.9077 (−2.6278) |
−7.4251 (−2.2398) |
−8.6339 (−2.5477) |
−17.6592 (−3.6279) |
−10.2529 (−3.0471) |
| Trade intensity: total | 0.0803 (0.8593) |
0.1006 (1.7311) |
0.0881 (1.4214) |
0.0461 (0.5066) |
0.0756 (1.3334) |
| Share return spreads | 0.5357 (1.1642) |
0.4882 (1.1574) |
|||
| Exchange rate deviations | −0.3230 (−1.3267) |
−0.2516 (−1.8416) |
−0.2741 (−1.9570) |
−0.4590 (−1.8297) |
−0.2607 (−1.6872) |
| Total industry structure | −0.1771 (−0.2610) |
−0.3663 (−0.5639) |
|||
| Country of legal origin: English | 0.4280 (1.2250) |
0.3945 (2.3354) |
|||
| Country of legal origin: French | 0.5505 (3.1641) |
0.4971 (3.9151) |
|||
| Country of legal origin: German | 0.1125 (0.4791) |
||||
| Country of legal origin: Scandinavian | −0.6751 (−1.9781) |
−0.5765 (−2.2501) |
|||
| Country of legal origin: all | 0.0731 (0.3807) |
0.2379 (2.0886) |
|||
| Accounting standards | 1.3197 (2.8772) |
0.9235 (2.6955) |
1.0469 (3.0074) |
1.8307 (3.9994) |
1.2382 (3.5733) |
| Structural reform | 0.1418 (1.1788) |
0.1974 (1.6414) |
|||
| Technology take-up | −0.8570 (−3.7580) |
−0.9134 (−4.3047) |
−0.8021 (−3.6317) |
−0.8808 (−3.7581) |
−0.8684 (−4.0648) |
| Adjacency | 0.1099 (0.4888) |
0.2860 (1.3104) |
0.3191 (1.7668) |
||
| Linguistic | 0.5259 (1.8906) |
0.3586 (2.9177) |
0.1988 (0.7397) |
||
| OI restrictions | – | 0.459 | 0.096 | – | 0.196 |
| Instrument quality | 0.351 | 0.727 | 0.727 | 0.344 | 0.742 |
| 0.250 | 0.740 | 0.740 | 0.236 | 0.755 | |
| 0.294 | 0.282 | ||||
| DWH | 0.432 | 0.896 | 0.986 | 0.657 | 0.942 |
| Correlation | 0.569 | 0.572 | 0.563 | 0.624 | 0.622 |
| Sigma | 0.482 | 0.471 | 0.476 | 0.450 | 0.442 |
|
Notes: As for Table 5. Equations (1) and (4) are exactly identified. |
|||||
In columns (4) and (5) we allow for legal origin to have different effects depending upon where it derived from – English, French, German and Scandinavian. Deleting the insignificant variables (other than trade) gives the model under column (5). Of the four legal origin dummies only that for German is not significant. For pairs of countries with legal systems of English and French origin there is a positive effect on the output correlation, while possessing a system of Scandinavian origin acts to reduce the correlation for country pairs. Finally for this specification common language is not significant but adjacency is.
As an additional check on the robustness of the results in Table 6 we examined whether foreign direct investment (FDI) might perform better than trade intensity in the general models. Recall that the results obtained from the more restricted models (see Tables 2 to 5) give some reason to think this might be the case. We tried two experiments. Initially we simply re-estimated all the models in Table 6 with FDI in place of trade intensity. This produced results (not reported) that are very similar to the ones in Table 6. There is no evidence from the more general models that use of FDI rather than trade intensity markedly improves their performance. In the second experiment we included both FDI and trade intensity in each of the models in Table 6. While the high correlation between the two variables produces relatively low t-statistics, we find no evidence that FDI statistically dominates trade intensity.
The results in Table 6 suggest that the following variables are jointly important for explaining bilateral output growth correlations: bilateral trade intensity; bilateral exchange rate volatility; accounting standards and speed of adoption of new information and communication technology. In addition various subsets of the following three variables: a common origin of the legal system; a common language and a common land border are found to be important. It is also evident from Table 6 that including the country characteristic variables into the model produces a considerably better fit of the data. For example, the best fitting model in Table 5 had a correlation between predicted and actual of 0.39, while those in Table 6 have numbers around 0.6. It is also the case that over-identifying restrictions are not rejected for models (2), (3) and (5) in Table 6.
One question that arises from these results is exactly how we should interpret the role played by the characteristic variables. One view, that is consistent with how we initially motivated the inclusion of these variables, is that they capture the extent to which pairs of countries might be susceptible to common shocks. Under this interpretation, the models in Table 6 explain bilateral output growth correlations as arising from both shock transmissions between countries via trade and monetary policy, and common shocks. There are other interpretations, however. It is possible that the characteristic variables capture interactions between economies that are not directly picked up by the existing transmission channel variables. In particular, an important way in which countries interact is via the interchange of ideas, information and beliefs. We have no direct measure of the importance of such information flows. Perhaps variables like common language, common land border and common legal systems act, in part at least, as proxies for unmeasured communication among countries. Finally it is also possible that our measures of particular transmission channels such as trade in goods are less than perfect and this is captured by the country characteristics.
3.4.1 Further analysis
It is apparent from the results in Table 6 that we have been able to identify a number of statistically significant variables that help to explain the cross-section variation in output growth correlations among OECD nations. However what is not apparent from the regression equations is exactly how well (or badly) these models do in fitting the observed correlation for a particular pair of countries. In particular, one thing of interest is the ability of the estimated models to explain the relatively high pair-wise correlations among the English-speaking countries. To address these issues, we report in Table 7 the actual and predicted correlations for all pairs of countries in our sample. The predicted values are obtained from the model in column (3) of Table 6 that includes; trade, exchange rate deviations, (aggregated) country of legal origin, accounting standards and technology take-up. We prefer this model since it does not include any variable that acts like a dummy variable for the English-speaking countries. In Table 7 shading indicates the ten pairings for the five English-speaking countries.
| Country pair | Actual | Predicted | Country pair | Actual | Predicted | Country pair | Actual | Predicted |
|---|---|---|---|---|---|---|---|---|
| Notes: Predicted values are from model (3) in Table 6 after transformation to correlations as described in Appendix A. Shaded cells are English-speaking country pairs. | ||||||||
| GB: US | 0.56 | 0.43 | CH: US | 0.35 | 0.28 | FI: JP | 0.19 | 0.18 |
| AT: US | −0.02 | 0.02 | CH: GB | 0.04 | 0.39 | ES: US | 0.30 | 0.07 |
| AT: GB | 0.12 | 0.22 | CH: AT | 0.35 | 0.34 | ES: GB | 0.48 | 0.29 |
| DK: US | 0.17 | 0.28 | CH: DK | −0.15 | 0.32 | ES: AT | 0.53 | 0.19 |
| DK: GB | 0.15 | 0.33 | CH: FR | 0.49 | 0.31 | ES: DK | −0.03 | 0.09 |
| DK: AT | −0.05 | 0.16 | CH: DE | 0.48 | 0.46 | ES: FR | 0.75 | 0.52 |
| FR: US | 0.19 | 0.11 | CH: IT | 0.68 | 0.25 | ES: DE | 0.61 | 0.32 |
| FR: GB | 0.39 | 0.33 | CH: NL | 0.55 | 0.34 | ES: IT | 0.53 | 0.41 |
| FR: AT | 0.51 | 0.35 | CH: NO | 0.16 | 0.29 | ES: NL | 0.57 | 0.37 |
| FR: DK | −0.10 | 0.30 | CH: SE | 0.36 | 0.37 | ES: NO | −0.08 | 0.12 |
| DE: US | 0.20 | 0.11 | CA: US | 0.85 | 0.59 | ES: SE | 0.54 | 0.21 |
| DE: GB | 0.08 | 0.33 | CA: GB | 0.54 | 0.51 | ES: CH | 0.34 | 0.15 |
| DE: AT | 0.61 | 0.71 | CA: AT | −0.03 | 0.09 | ES: CA | 0.32 | 0.11 |
| DE: DK | 0.01 | 0.35 | CA: DK | 0.09 | 0.16 | ES: JP | 0.28 | 0.18 |
| DE: FR | 0.50 | 0.45 | CA: FR | 0.25 | 0.20 | ES: FI | 0.29 | 0.17 |
| IT: US | 0.33 | 0.09 | CA: DE | 0.12 | 0.20 | AU: US | 0.66 | 0.53 |
| IT: GB | 0.34 | 0.31 | CA: IT | 0.52 | 0.18 | AU: GB | 0.37 | 0.40 |
| IT: AT | 0.39 | 0.29 | CA: NL | 0.52 | 0.23 | AU: AT | −0.08 | −0.10 |
| IT: DK | −0.02 | 0.16 | CA: NO | 0.30 | 0.28 | AU: DK | 0.05 | 0.17 |
| IT: FR | 0.61 | 0.47 | CA: SE | 0.45 | 0.32 | AU: FR | 0.23 | 0.05 |
| IT: DE | 0.52 | 0.37 | CA: CH | 0.49 | 0.24 | AU: DE | −0.02 | 0.07 |
| NL: US | 0.57 | 0.19 | JP: US | −0.07 | 0.14 | AU: IT | 0.34 | 0.05 |
| NL: GB | 0.30 | 0.40 | JP: GB | 0.07 | 0.27 | AU: NL | 0.39 | 0.07 |
| NL: AT | 0.51 | 0.46 | JP: AT | 0.18 | 0.29 | AU: NO | 0.17 | 0.31 |
| NL: DK | 0.20 | 0.34 | JP: DK | −0.37 | 0.08 | AU: SE | 0.34 | 0.35 |
| NL: FR | 0.43 | 0.53 | JP: FR | 0.28 | 0.24 | AU: CH | 0.43 | 0.17 |
| NL: DE | 0.66 | 0.58 | JP: DE | 0.38 | 0.37 | AU: CA | 0.72 | 0.43 |
| NL: IT | 0.49 | 0.42 | JP: IT | 0.32 | 0.20 | AU: JP | −0.07 | 0.16 |
| NO: US | 0.26 | 0.42 | JP: NL | 0.04 | 0.23 | AU: FI | 0.41 | 0.31 |
| NO: GB | 0.11 | 0.43 | JP: NO | −0.22 | 0.13 | AU: ES | 0.21 | −0.05 |
| NO: AT | 0.06 | 0.06 | JP: SE | 0.12 | 0.21 | NZ: US | 0.35 | 0.47 |
| NO: DK | 0.49 | 0.48 | JP: CH | 0.32 | 0.30 | NZ: GB | 0.22 | 0.45 |
| NO: FR | −0.26 | 0.24 | JP: CA | −0.03 | 0.26 | NZ: AT | −0.28 | −0.09 |
| NO: DE | 0.14 | 0.26 | FI: US | 0.30 | 0.38 | NZ: DK | 0.31 | 0.19 |
| NO: IT | 0.30 | 0.17 | FI: GB | 0.48 | 0.44 | NZ: FR | −0.17 | 0.09 |
| NO: NL | 0.31 | 0.28 | FL: AT | −0.10 | 0.12 | NZ: DE | −0.29 | 0.11 |
| SE: US | 0.37 | 0.42 | FI: DK | 0.02 | 0.49 | NZ: IT | 0.00 | 0.07 |
| SE: GB | 0.57 | 0.47 | FI: FR | 0.42 | 0.26 | NZ: NL | 0.12 | 0.12 |
| SE: AT | 0.25 | 0.15 | FI: DE | −0.11 | 0.29 | NZ: NO | 0.40 | 0.22 |
| SE: DK | 0.28 | 0.54 | FI: IT | 0.40 | 0.23 | NZ: SE | 0.18 | 0.35 |
| SE: FR | 0.54 | 0.28 | FI: NL | 0.12 | 0.30 | NZ: CH | 0.00 | 0.20 |
| SE: DE | 0.26 | 0.31 | FI: NO | 0.07 | 0.54 | NZ: CA | 0.38 | 0.38 |
| SE: IT | 0.62 | 0.28 | FI: SE | 0.66 | 0.65 | NZ: JP | −0.23 | 0.19 |
| SE: NL | 0.33 | 0.32 | FI: CH | 0.39 | 0.36 | NZ: FI | 0.24 | 0.28 |
| SE: NO | 0.27 | 0.60 | FI: CA | 0.48 | 0.28 | NZ: ES | −0.22 | −0.01 |
| NZ: AU | 0.50 | 0.52 | ||||||
It is apparent from Table 7 that the model has difficulty in fitting the negative correlations in the data. This is mainly a problem for pairings with Japan and New Zealand. The most likely explanation for the high frequency of low and negative bilateral correlations observed for these two countries is that they have been affected by idiosyncratic shocks that have not been transmitted, either directly or indirectly, to the other countries in our sample. At least for New Zealand, the lack of transmission of home grown shocks from this small economy is certainly consistent with our prior expectation.
Turning to the English-speaking economies, the model does best at fitting the correlations for New Zealand and Australia, New Zealand and Canada, UK and Canada, and UK and Australia. It does worst at fitting Canada and Australia. In general the model under-predicts the degree of correlation among the English-speaking countries. The only exception to this is for New Zealand, which the model implies should be more highly correlated with both the US and the UK. Again this may be a reflection of idiosyncratic shocks in New Zealand.
In the case of Australia and the US our model predicts a correlation of 0.53 compared with the actual value 0.66. To get an indication of how the explanatory variables in our model contribute to the predicted correlation we employ a simple decomposition. Consider the following estimated model where the variables are written in terms of deviations from their means.
If we sequentially set all the explanatory variables except one equal to their respective means, then we can identify the individual contribution of each variable to the predicted value of y (relative to its mean value). In our case we have to apply the transformation in Appendix A, but using the above idea we can identify how each of the variables contributes to the predicted US–Australian correlation of 0.53.
Table 8 reports the results of this decomposition. If all of the US–Australian observations for trade intensity, exchange rate deviations, (aggregated) country of legal origin, accounting standards and technology take-up were equal to the sample means for these variables we would expect a bilateral output growth correlation of 0.29. Thus the five variables in the model contribute a total of 0.24 to the predicted correlation. Reading across Table 8 indicates the individual contribution of each of the variables to explaining the predicted US–Australian growth correlation.
| Trade intensity | Exchange rate deviations |
Country of legal origin: all |
Accounting standards | Technology take–up |  |
|
|---|---|---|---|---|---|---|
| Contribution | 0.04 | −0.02 | 0.08 | 0.06 | 0.08 | 0.24 |
| Percentage | 17 | −8 | 33 | 25 | 33 | 100 |
|
Notes: Contributions are based upon the coefficient estimates from Table 6 model (3). They indicate how much each variable contributes to the predicted Australian–US correlation (less the estimated mean correlation). The second row reports the contribution in percentage terms. Contributions are calculated after transforming the correlations as described in Appendix A. Note that the estimated mean correlation (0.29) differs slightly from the sample mean for the data, 0.27; this arises because of the non-linear transformation used in estimation. |
||||||
The intensity of trade between Australia and the US make a relatively small positive contribution (0.04) to the correlation. This supports the widely accepted view that bilateral trade in goods between Australia and the US is not the full story in explaining the observed correlation between these countries. By way of comparison, the predicted correlation for Canada and the US is 0.59, which is 0.30 larger than the mean correlation across all country pairs of 0.29. Of this, about 0.12 is contributed by trade intensity (again based on column (3) of Table 6).
Now consider the effect of bilateral exchange rate volatility for Australia and the US. This has actually acted to reduce the correlation in growth rates by 0.02. Again it is interesting to consider the Canada–US results. In this case the relatively low bilateral exchange rate volatility between the two countries contributes 0.08 towards their observed correlation.
According to Table 8 the explanation for the high Australian–US growth correlation primarily lies with the characteristics and institutions that the two countries share. The existence of legal systems with a common English origin in Australia and the US adds a predicted 0.08 to the two countries output growth correlation. A similar contribution is obtained from the technology take-up variable. Our indicator of the speed of adoption of new ICT gives Australia and the US equal scores. The index of joint accounting standards for Australia and the US contributes 0.06. In aggregate these three variables contribute 0.22 (out of 0.24) to the predicted Australian–US output growth correlation.
Before concluding it is useful to consider what our empirical model suggests about the likely magnitude of the Australia–US output growth correlation in the future. In particular, are we likely to see a continuation of the high positive correlation of the past twenty years? According to the model two things that would make Australia more susceptible to shocks of US origin and tend to raise the degree of output correlation are increased bilateral trade and lower volatility of the USD/AUD exchange rate. At present however significant changes in these variables (in the required directions) seem unlikely.
More important for explaining the strong Australia–US growth correlation are the characteristic or institutional variables. While the nature of these variables is such that they are unlikely to undergo rapid changes, their expected future contribution to the Australian–US correlation depends on the reason for their current significance. If the characteristic variables actually measure the susceptibility of the Australian and US economies to similar types of economic shocks then most of the recent strong Australian–US output growth correlation is due to common shocks. Consequently whether this strong correlation will continue depends on the relative importance of common verses country-specific shocks in driving each country's output. It is certainly consistent with our results to argue that if either Australia or the US were to be hit by a sequence of large idiosyncratic shocks then the observed output correlation between the two countries could fall to near the OECD average.
Alternatively however, the significance of the characteristic variables in our model may reflect the omission of important transmission channels between pairs of countries. Under these circumstances the majority of the Australian–US output correlation is likely to be due to the transmission of non-trade and non-monetary policy shocks from the US to Australia. In these circumstances there is little reason to expect the existing degree of correlation between Australian and US output growth rates to fall in the future.
Footnotes
This argument is investigated more thoroughly in Canova and Dellas (1993). [10]
Frankel and Rose (1998) discuss this issue further; notice that the argument presumes that trade is primarily characterised by inter-industry rather than intra-industry trade. Two further points are also in order with respect to this prediction. First, if industry specific shocks are important, we might expect less specialization to avoid the effects of these shocks. Second, relative price effects can offset this to some extent, a point made by Cole and Obstfeld (1991). [11]
Alternative measures that have been used are total bilateral trade as a share of total trade and total bilateral trade as a share of aggregate GDP; see Frankel and Rose (1998). The first suffers from not measuring the relative importance of trade in the overall economy. The second suffers from obscuring one-way interdependence. [12]
A natural direction to consider would be to include both the export and import intensity together. Because the two series are highly correlated such a model is not well behaved; however, the results clearly suggest the dominance of the export intensity measure. [13]
The instruments used are the following: the natural logarithm of the distance between two countries; a dummy variable for whether the two countries are adjacent; a dummy variable for whether the two countries share a common language; a dummy variable for whether two countries share a particular common legal origin (English, French, German or Scandinavian); a bilateral index of accounting standards; and a bilateral index of the concentration of firm ownership. The geographic and language variables are from Frankel and Rose (1998) and are typical variables used in gravity models for bilateral trade, hence their use as instruments here. The common legal origin variables, the accounting standard variable, and the firm ownership variable are measures related to corporate governance and are taken from La Porta et al (1998). These instruments are included in part because they may explain bilateral trade but also because they may explain (or at least be correlated with) bilateral trade in assets or common policy behaviour. We initially use a fixed set of instruments for all IV regressions, which explains why they are included here. [14]
In their study of trade and growth, Frankel and Romer (1999) obtain a similar result for, we suspect, similar reasons to that here; see this study for a more complete discussion of this issue. [15]
A further possibility is countries have a high degree of FDI between them as a consequence of firms attempting to reduce the risk they face by expanding and diversifying into markets with different cyclical patterns. In this case, we might suspect that FDI is inversely related to business cycle correlations. This is analogous to the argument that trade intensities will be inversely related to business cycle correlations as different countries specialise in different industries to capture gains from comparative advantage. The results in Tables 2 and 3 do not support these arguments, however. [16]
We take the natural logarithm of all three measures. Full details on the construction of these series are presented in Appendix B. We have also considered mean absolute values of these spreads as a measure of financial integration. This provides very similar results; econometrically, the standard deviation measure is somewhat better behaved. [17]
This depends of course upon the quality and validity of the instruments; the instrument set are those described in the previous section. [18]
There is some evidence that flexible exchange rates do not provide this insulation role, see Artis and Ehrmann (2000). [19]
Clark and van Wincoop (1999) consider a similar measure in their examination of bilateral output correlations for 14 EU economies. They find that once trade intensity and country size are controlled for, interest rate differentials are not a significant explanation of output correlations. [20]
Buiter (2000) argues that movements in exchange rates are themselves an important source of shocks. If so, on a bilateral basis this would have asymmetric effects for two economies and consequently lower bilateral output correlations. Frankel and Rose (1998) also consider the role of a fixed versus flexible exchange rate regime as a potential explanation for bilateral output correlations. They use both a dummy variable approach and one based on actual bilateral exchange rate volatility but find no significant effects after controlling for the effect of trade. [21]
The standard deviation of the quarterly log difference of the exchange rate for these two countries is 0.1 per cent. We use a specific example rather than set the exchange rate volatility to zero since the model is estimated using the natural logarithm of the standard deviation of the bilateral exchange rate, which is undefined when there is no exchange rate volatility. [22]
Against this, however, is a substantial empirical literature that finds little evidence that exchange rate volatility reduces the level of international trade; see Gagnon (1993). [23]
In his study, which uses 21 OECD countries for the period 1959–1993, Imbs finds that his manufacturing-based index has a strong significant negative relationship with bilateral growth correlations. Moreover, this variable dominates the contribution of bilateral trade intensities – which is a very strong result. For our sample of data, however, we have not been able to replicate Imbs' findings. [24]
We use OLS for this model as we do not believe that industry structure is an endogenous variable in our cross-country model. [25]
In this instance, we do not measure the distance between the quality of accounting standards for two countries. If only one country has well-designed and transparent accounting standards then this may be sufficient to promote greater integration between two countries. High quality accounting standards in one country may be able to compensate for relatively lower standards in the other country. [26]
Shleifer (1986) provides a slightly more sophisticated explanation for the role of technology in driving economic cycles. Firms with some degree of market power may choose to implement new technologies when economic growth is strong, ensuring that the size of the market and monopoly profits are larger. This leads to an exacerbation of the business cycle. Notice that this complicates the interpretation; underlying the explanation is some non-specified source of business cycle fluctuations which then receive additional impetus from the firms' behaviour. [27]
The set of instruments is now: the natural logarithm of the distance between two countries; the bilateral index of the concentration of firm ownership; the geometric average of median incomes from 1980–2000. The first two are instruments used previously; median income, which is a standard instrument in gravity models of trade, is included as we wish to consider a number of previous instruments as explanatory variables. [28]