RDP 2004-09: Co-Movement of Australian State Business Cycles 5. Model Results
October 2004
- Download the Paper 739KB
It is important to emphasise that our model results must be interpreted with caution, given the limited amount of data available and the well-known sensitivity of Kalman filters to assumptions and initial conditions. Thus our focus here is on the patterns of behaviour of the common, idiosyncratic and spillover components, and the stylised facts arising from these, rather than on the precise coefficient estimates and quantitative implications of the model. While we believe the model provides a fair representation of the data, there is simply not enough historical information on Australian state activity to draw reliable quantitative conclusions. Bearing this caveat in mind, however, the model results support the findings we reported in Section 3, providing evidence that common shocks, rather than spillovers of lagged shocks between states, are primarily responsible for the observed co-movement of state cycles. We focus here on the results for SFD; the results for hours worked are quite similar and are provided in Appendix B.
The estimates for δ, in the first two columns of Table 3, suggest that trend growth in SFD picked up in all states during the 1990s, in some cases substantially.[20] This accords with our priors: the period since the recession has seen higher average productivity growth nationally, and stronger growth in every state.
| State | Trend parameter, 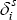
|
Common cycle response parameter, 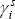 |
|
|---|---|---|---|
| 1985:Q4–1994:Q4 | 1995:Q1–2003:Q2 | ||
| NSW | 2.59 | 3.61 | 1 |
| Vic | 1.68 | 4.76 | 1.06 |
| Q1d | 3.81 | 4.47 | 1.19 |
| WA | 3.18 | 4.16 | 1.36 |
| SA | 1.59 | 3.63 | 1.15 |
| Tas | 1.43 | 2.33 | 1.19 |
| National average | 2.51 | 4.09 | 1.10 |
|
Notes: Trend parameter estimates can be interpreted as average annualised percentage trend growth rates. The national cycle response parameter for NSW is normalised to be 1. The ‘national average’ figures are calculated as the average of the state figures, weighted by their share of total SFD. |
|||
We begin our analysis of the estimated cycles with the common cycle, which influences activity
in all states. Recall that the extent to which SFD in state i responds to the common
cycle is governed by the parameter 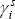 , so the magnitude of the common
cycle effect varies across states. Figure 5 shows the estimated common cycle multiplied by the
weighted average of the parameters
, so the magnitude of the common
cycle effect varies across states. Figure 5 shows the estimated common cycle multiplied by the
weighted average of the parameters 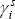 , where the weights are the
states' shares of total SFD. This can be thought of as the common cycle of all states
combined, or the common component of domestic final demand, excluding final demand in the two
territories.
, where the weights are the
states' shares of total SFD. This can be thought of as the common cycle of all states
combined, or the common component of domestic final demand, excluding final demand in the two
territories.
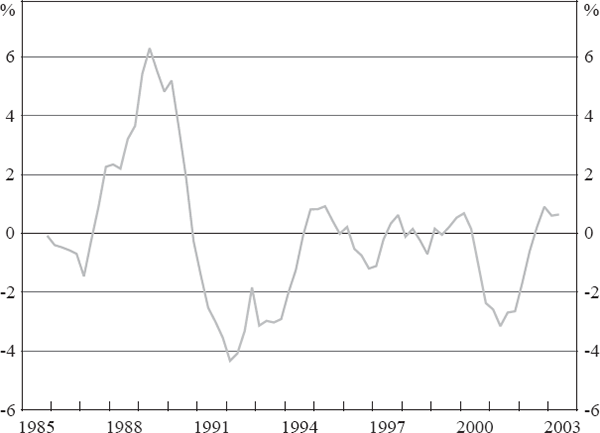
Note: Graph depicts the weighted average common cycle for SFD across states, where the average is calculated using states' shares of total SFD as the weights.
Although the estimated common cycle should be interpreted with our earlier caveat in mind, it matches many of the stylised facts about the Australian business cycle over the past 20 years.[21] The property and investment boom in Australia in the late 1980s and the subsequent recession are reflected in the estimated cycle peaking in June 1989 at 6 per cent above trend, before falling to levels indicating below-trend activity.[22] The cycle remains negative until mid 1994, before settling around zero over the remainder of the 1990s. (Note that this near-zero level does not imply weak growth, but rather less volatile growth at a stronger trend rate.) The final major feature is a dip below trend in late 2000, consistent with the swings in housing construction associated with the introduction of the GST in July 2000. Recent conditions indicated by the model can be characterised as around trend.
Estimates of the responsiveness of states to the common cycle for SFD, 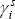 , are
presented in the last column of Table 3.[23]
The degree of responsiveness of different states to the common cycle generally accords with our
priors and with previous research. The estimated response coefficients are similar for all
states, suggesting that the common cycle has quite a uniform impact. Nevertheless, there appears
to be a tentative relationship between openness and degree of sensitivity to the common cycle.
Western Australia, which has the most open economy and is therefore most exposed to exchange
rate shocks (Weber 2003, p 2), also has the strongest response. The two least open states, NSW
and Vic, are the least responsive, consistent with the idea that fluctuations in the exchange
rate and the terms of trade are major types of common shock for a small open economy. Regions
with greater openness would be expected to be more sensitive to these shocks than less open
regions.
, are
presented in the last column of Table 3.[23]
The degree of responsiveness of different states to the common cycle generally accords with our
priors and with previous research. The estimated response coefficients are similar for all
states, suggesting that the common cycle has quite a uniform impact. Nevertheless, there appears
to be a tentative relationship between openness and degree of sensitivity to the common cycle.
Western Australia, which has the most open economy and is therefore most exposed to exchange
rate shocks (Weber 2003, p 2), also has the strongest response. The two least open states, NSW
and Vic, are the least responsive, consistent with the idea that fluctuations in the exchange
rate and the terms of trade are major types of common shock for a small open economy. Regions
with greater openness would be expected to be more sensitive to these shocks than less open
regions.
In addition to the effect of the common cycle, the overall cycle in each state is partly driven by fluctuations specific to that state, which are captured in its idiosyncratic cycle, as shown in Equation (4).[24] One way of determining the relative importance of common and idiosyncratic shocks to state cyclical activity is to compare the contributions of the two terms on the right-hand side of Equation (4) to each state's overall cycle, cit.
Figure 6 shows each state's overall cycle, graphed as a line, with the bars representing the common and idiosyncratic contributions to the overall cycle. In all states, the common cyclical component tends to be more important than the idiosyncratic component. Table 4 summarises the contributions of these components to the variance of the overall cycles. For the larger states (NSW, Vic and Q1d), the common cycle makes a greater contribution than the idiosyncratic cycle, which suggests that state-specific shocks are less important for these states. For the smaller states (SA, WA and Tas), the contributions of both components are quite similar. This similarity may, however, partly reflect the model's identification assumptions; some shocks we think of as common (such as exchange rate movements) may affect states with different lags and thus be partly attributed to each state's idiosyncratic cycle. The greater volatility of activity in the smaller states may also show up in a larger idiosyncratic component. Indeed, it is interesting to note that common shocks still have a larger influence on these states' cycles than on those of the larger states.
| State | Common cycle component – ppt | Idiosyncratic cycle – ppt | Overall cycle |
|---|---|---|---|
| NSW | 5.5 | 2.1 | 7.4 |
| Vic | 6.1 | 2.9 | 12.2 |
| Q1d | 7.7 | 1.5 | 8.8 |
| WA | 10.0 | 13.8 | 27.1 |
| SA | 7.2 | 5.3 | 9.1 |
| Tas | 7.7 | 7.8 | 11.6 |
|
Note: The sum of a state's common and idiosyncratic cycle variances need not equal the overall cycle variance because they may have a non-zero covariance. |
|||
These results suggest that common shocks are the primary contributors to cycles in state activity, although idiosyncratic shocks also play an important role. The fact that idiosyncratic shocks appear to make a larger contribution to activity in the smaller states could reflect behavioural differences, but we feel it is more likely to be explained by differences in the timing of states' responses to shocks such as exchange rate fluctuations.
Finally, we turn to spillovers as a third source of fluctuations in state activity. To assess the role and behaviour of spillovers in the model, we examine the impulse response functions implied by Equation (6), which trace the effects over time of a 1 per cent shock to one state's idiosyncratic cycle on the cycles of the other states. These impulse response functions are presented in Figure B1 of Appendix B. Unfortunately the functions are not well-behaved, primarily because the estimated response coefficients for WA and, to a lesser extent, Q1d cause them to respond with implausible strength to shocks in other states. For example, positive shocks to NSW have a negative and destabilising influence on WA's activity, with a 1 percentage point shock to NSW's cycle reducing activity in WA by 4.7 per cent in the first year alone. The other states' responses are also then contaminated, to some extent, through flow-on effects. (We could find no outliers in the data to explain these large coefficients; as discussed before, they may arise in part from differences in the timing of state responses to shocks like fluctuations in the exchange rate.) These problems appear to stem from the small sample available and the complexity of the model, which make it especially difficult to accurately estimate the large number of parameters describing the interaction effects between state idiosyncratic cycles. To mitigate the problem somewhat, we also calculate impulse responses from the estimated coefficients, but with the response coefficients for WA and Q1d set to zero. This is equivalent to ‘disconnecting’ these two states from the system, so they do not respond to shocks in other states. The resulting impulse response functions (Figure B2) are much more sensible. However, they are generally quite small and unlikely to be statistically significant.
To avoid some of these problems, we can instead focus on the longer-term cumulative effects of cyclical shocks on activity. Table 5 shows the cumulative gain in SFD for each state (analogous to a ‘change in wealth’ measure) in the eight quarters following a temporary 1 per cent shock to one state's idiosyncratic cycle.
| State | Cumulative effect after eight quarters of a shock to: | ||||||
|---|---|---|---|---|---|---|---|
| NSW | Vic | Q1d | WA | SA | Tas | National | |
| NSW | 4.5 | −1.0 | −1.1 | −0.6 | −1.1 | −1.2 | 5.9 |
| Vic | 1.1 | 1.8 | −1.0 | 0.1 | −2.8 | −0.6 | 6.3 |
| Q1d | 1.7 | 0.3 | 2.5 | 1.6 | 1.3 | 1.1 | 7.1 |
| WA | −8.6 | −2.7 | −1.8 | 2.2 | −2.7 | −0.8 | 8.0 |
| SA | 1.8 | 1.0 | 0.7 | −1.3 | 3.8 | 0.5 | 6.8 |
| Tas | 2.2 | 2.4 | 2.4 | −0.4 | 3.3 | 3.1 | 7.1 |
|
Notes: The cumulative response is effectively the integral between the shocked level of SFD and the no-shock counterfactual level from the shock quarter to the eighth quarter following the shock. The shocks to state idiosyncratic cycles are all 1.0 per cent. The shock to the common cycle is 0.91 per cent, which corresponds to an increase in aggregate final demand of 1 per cent in the shock quarter. (The shock applied is less than 1 per cent because the average state response to the common cycle is greater than one – see Table 3.) All shocks last one quarter, but the model dynamics imply a sustained decay path in each case. |
|||||||
In the last column of Table 5, we present the cumulative responses of state activity following a corresponding shock to the common cycle.
As with the impulse responses, the results for WA seem unrealistic. Aside from these, however, the most striking features are the cumulative effects of common shocks on activity, and the uniformity of these effects across states. The effect of a 1 per cent shock to the common cycle accumulates to an increase of between 5.9 and 8 percentage points in the level of SFD in each state over the shock quarter and the subsequent eight quarters. The size of this effect is due to the strong persistence of the common cycle, implying that common shocks provide repeated gains (or losses) in activity over a long period.
The bold diagonal elements in Table 5, measuring the long-term effect of idiosyncratic shocks on the state of origin, are also quite large (well above the initial shock of 1 per cent), although significantly smaller than the common shock effects. The off-diagonal elements, which characterise spillovers of shocks between states, are generally smaller than the corresponding own-state effects and in some cases have the opposite sign.[25] These results broadly support our earlier findings: common shocks appear the most important to activity, followed by idiosyncratic shocks, with spillovers playing a relatively minor role.
As a final robustness check, we tried replacing SFD with our own constructed estimates of quarterly gross state product (GSP). Full details are given in Appendix C. We found that making this change produced qualitatively very similar results to those from the SFD-hours worked model, even though the GSP estimates are a broader measure of activity.
Footnotes
In contrast, the estimated post-break trend growth rates for hours worked are all lower than the pre-break estimates. This suggests productivity growth in all states must have increased substantially during the 1990s, to reconcile the slowing of growth in hours worked with the increased trend growth rates of SFD. [20]
The estimated cycle has a correlation of 0.85 with Hodrick-Prescott filtered domestic final demand. [21]
This coincides with the peak in the dated Australian SFD cycle discussed earlier. [22]
The estimated coefficients for hours worked are around half the size, with an average coefficient of 0.52, compared with an average of 1.10 for SFD. [23]
Each state's SFD is assumed to respond one-to-one to its idiosyncratic cycle. As with the common cycle, we constrain hours worked to respond to the same idiosyncratic cycle as SFD, but allow the magnitude of response to vary by scaling parameters θi. These fluctuations are permitted to be contemporaneously correlated with shocks in other states. We separate the idiosyncratic cycle from the common cycle by defining the latter as affecting all states simultaneously. Hence a regional shock covering more than one state would be picked up in those states' idiosyncratic cycles rather than in the common cycle. [24]
The exceptions are: the figures for WA (which, as already discussed, we regard as unreliable); those for Tas (which may reflect its relatively small size); and the response of Vic to SA, which also appears to be an outlier. [25]