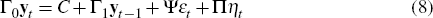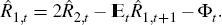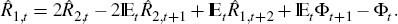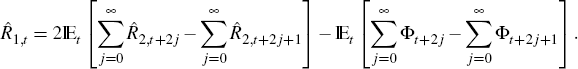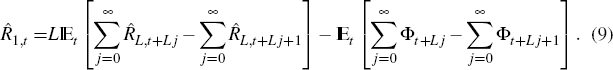RDP 2011-02: Long-term Interest Rates, Risk Premia and Unconventional Monetary Policy 3. Equilibrium Determinacy

A desirable property of a monetary policy rule is consistency with a unique equilibrium. Rules that fail to bring about a unique equilibrium are undesirable because they allow beliefs to turn into independent sources of business fluctuations. In other words, non-fundamental shocks may increase the volatility of equilibrium dynamics.^[6] In general, the variables for which there may be large fluctuations due to indeterminacy include those that enter loss functions, that is those that matter for measures of an economy's welfare. So, any rule that achieves a unique equilibrium should be thought better than any rule that does not.

The log-linear equations that characterise the model's equilibrium can be written, following Sims (2002), as

where ε_t is a l × 1 vector of fundamental serially uncorrelated random disturbances, the k × 1 vector η_t contains expectational errors, and the n × 1 vector y_t contains the remaining variables including conditional expectations.^[7] The matrices, C,Γ₀,Γ₁,Ψ and Π are of conformable dimensions. The number of generalized eigenvalues of Γ₀ and Γ₁ that are greater than one in absolute value is m. The values of the structural parameters that make it to the matrices Γ₀ and Γ₁ determine m. Cagliarini and Kulish (2008) show that

• if m = k, the solution to Equation (8) is unique;
• that if m < k there are infinitely many solutions that satisfy Equation (8);
• and that if m > k there is no stable solution that satisfies Equation (8).

We use these conditions to characterise regions of existence, uniqueness and multiplicity of the equilibrium in the space of the structural parameters, in particular, in the space of the parameters of the monetary policy rule.

Figure 2 shows regions of the policy parameter space where the equilibrium is unique, for the Taylor rule and for long-term interest rate rules of maturities 4, 12 and 40.^[8] The coefficients on inflation, ρ_π, and on output, ρ_y, vary; the remaining ones are fixed. The regions of uniqueness for long-term interest rate rules are large and as large as for the Taylor rule. The unshaded regions correspond to multiple equilibria or non-stationary equilibria. As in the conventional case, low responses to inflation lead to indeterminacy.

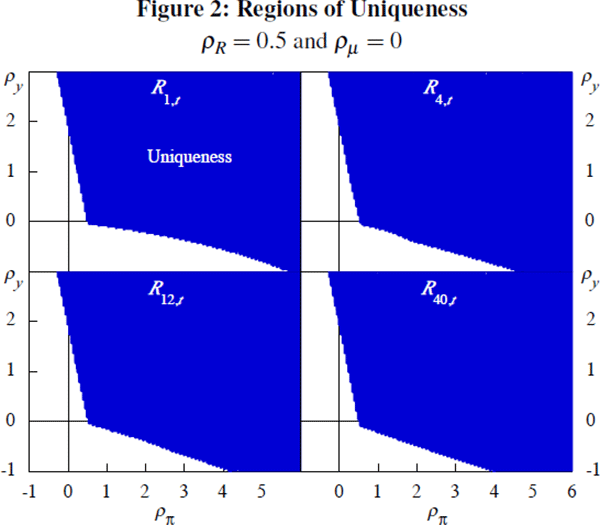
To explore equilibrium determinacy further, we compute regions of uniqueness in the space of ρ_R and ρ_π. Figure 3 shows that the Taylor principle holds for long-term interest rates. As the slope of the critical contour shows, uniqueness requires ρ_R + ρ_π > 1: that the long-run response of the interest rate to inflation exceeds unity.^[9] Figure 3 shows that these regions are also large. Our analysis suggests that unique allocations are as feasible for long-term interest rate rules as they are for Taylor rules. The regions of uniqueness remain large for a wide range of other parameter values.

It may seem surprising that a long-term interest rate rule can support a unique equilibrium as well as a short-term interest rate rule can with the expectations hypothesis and an endogenous risk premium at work.^[10] Imagine the central bank wishes to set 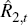. Because Equation (7) requires that 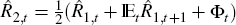, it may appear that, for a value of 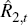, markets could find multiple ways in which to exhaust arbitrage opportunities, that is, multiple combinations of 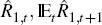and Φ_t that result in 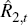. This argument suggests that the ability of a long-term interest rate rule to achieve a unique equilibrium should be impaired. But, it is not.

Typically, we think of the expectations hypothesis as short rates determining long rates. But it is important to recognise that the expectations hypothesis works the other way: long rates can determine short rates too. To see this take Equation (7) for 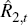and rewrite it as a first-order, stochastic, difference equation in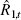

Advance the equation one period and substitute the resulting expression back to obtain,

Continue in this way to find the alternative expression for the short-term interest rate,

The expression above shows that if a rule for 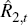supports a unique equilibrium, then it determines uniquely an expected path of the risk premium, Φ_t, and an expected path of the long rate, 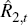. These paths simultaneously pin down the current level of the short rate, 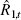. This argument, generalised to an interest rate of an arbitrary maturity, 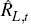, gives the expression below

So, if the policy rule is consistent with a unique equilibrium, then there exists expected paths of the monetary policy instrument and of the risk premium, as given by Equation (9), that pin down interest rates of shorter and longer maturities.

The unique equilibrium of long-term interest rate rules is quite an important result. Fluctuations in risk premia are always found in the data.^[11] So, imagine then, contrary to what has just been shown, that with an endogenous risk premium a long-term interest rate rule would always fail to achieve a unique equilibrium. This means that even if we were to obtain a unique outcome with the shortest of interest rates – a quarterly interest rate in a quarterly model and monthly interest rate in a monthly model – this unique outcome would not translate into a unique outcome at any higher frequency. Results from quarterly models or from monthly models would have no bearing on the real world, where monetary policy sets an overnight interest rate. But apart from the relief that the uniqueness of long-term interest rate rules may give to modellers, what's perhaps as significant is the support that the result gives to long-term interest rates as candidate instruments of monetary policy.

Long-term interest rate rules support unique equilibria as well as Taylor rules. But what dynamics do they imply? This question is taken up next.

Footnotes

See, for example, Lubik and Schorfheide (2004), Jääskelä and Kulish (2010) and the references therein. [6]

The expectational error for a variable x_t is 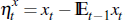[7]

Under the Taylor rule, the friction applies at maturity 12. For the long-term interest rate rules, the friction applies at the set interest rate. [8]

It is an approximate version of the Taylor principle, because as seen in Figure 2 the slope of contour is not exactly vertical. The condition ρ_R + ρ_π > 1 would hold exactly if the other parameters in the rule were zero. [9]

McGough et al (2005) find that long-term interest rate rules often result in indeterminacy; more than our numerical analysis suggests. The main reason for this difference is that the long-term interest rate rules that we analyse allow for interest rate smoothing and for a response to output. Both of these, but especially the response to the lagged value of the interest rate instrument, significantly expand the regions of uniqueness. [10]

See Cochrane and Piazzesi (2005) and the references therein. [11]