RDP 2012-07: Estimates of Uncertainty around the RBA's Forecasts 3. Estimates of Forecast Uncertainty

Forecast errors can be summarised in various ways. The root mean squared error (RMSE) is a standard measure of the ‘typical’ forecast error, with useful statistical properties. Figure 2 shows RMSEs for the four variables at different horizons.

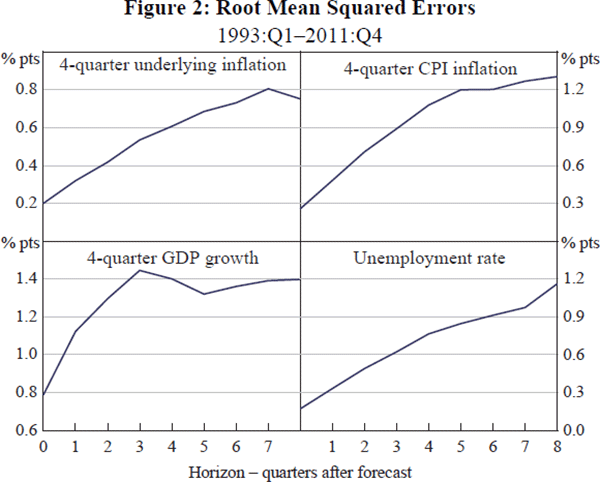
One popular way of presenting forecast uncertainty is through a confidence interval or fan chart, in which a margin of error is added to either side of the central forecast. RMSEs are often used for this purpose. If forecast errors are normally distributed, there is about a two-thirds probability that actual outcomes will fall within one RMSE of the forecast, and about a 95 per cent probability that they fall within two RMSEs of the forecast.

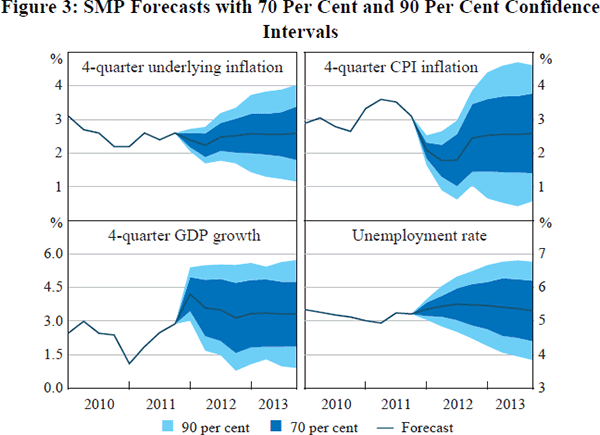
An alternative approach is to use quantiles (such as deciles or percentiles) of the distribution of historical forecast errors. Figure 3 shows 70 per cent and 90 per cent confidence intervals constructed by adding the 70^th and 90^th percentile of absolute forecast errors at each horizon on either side of the February 2012 SMP forecast. As a guide to interpretation, consider the 90 per cent interval for underlying inflation in the year-ended 2013:Q4, shown in the top left panel. This indicates that, if forecast errors are the same size as in the past then, at the time of the forecast, there was a 90 per cent probability that underlying inflation in the year ended 2013:Q4 would lie between 1.2 per cent and 4.0 per cent. In Appendix C, we present tables of the 70^th, 90^th and other percentiles, so that confidence intervals can be constructed about future forecasts.

In Section 5.4 we compare RMSEs with empirical quantiles. For our dataset the two approaches give very similar estimates. For most purposes, the choice between them is essentially presentational, and we alternate between the measures in the following sections.

In constructing the confidence intervals in Figure 3 we have made many assumptions. For example, in using absolute errors, we have assumed that the confidence intervals are unbiased and symmetric. However, we have not assumed that the errors are normally distributed. We discuss these and other possible assumptions in Section 5. There are many other ways that forecast uncertainty can be measured and presented. This is illustrated in Appendix A, which describes measures of uncertainty presented by other central banks.