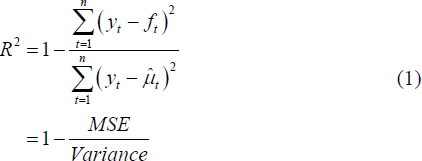RDP 2012-07: Estimates of Uncertainty around the RBA's Forecasts 4. How Do These Estimates Compare?
November 2012 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 690KB
The confidence intervals in Figure 3 strike many observers as wide, particularly for GDP growth. In other words, our estimates of uncertainty are surprisingly high.
Initial impressions presumably reflect comparisons with subjective estimates of uncertainty. Psychological studies find that subjective estimates of uncertainty are regularly too low, often by large margins. People have a systematic bias towards overconfidence.[2] Accordingly, in the absence of objective information, the general public may expect an unrealistically high standard of forecast accuracy.
However, the impression of high uncertainty is also consistent with comparisons to external benchmarks, to which we now turn. The intention in making these comparisons is not to run ‘horse races’ but to help interpret uncertainty about the forecasts.
4.1 Verbal Descriptions of the Forecast
The simplest benchmark is common, qualitative descriptions. The intervals in Figure 3 span outcomes that would be described very differently. For example, the 90 per cent confidence interval for GDP growth in the year ended 2013:Q4 extends from 0.9 per cent to 5.7 per cent. That is, although the central forecast is for growth to be moderate, it could easily turn out to be very strong, or quite weak. Similarly, while little change in the unemployment rate is expected, a large increase or decrease is possible. Although the most likely outcome for headline inflation is within the RBA's target range, it could easily be well outside. In comparison, we can be somewhat more confident about underlying inflation, which is likely to remain moderately close to the target range.
Verbal descriptions are simple and meaningful for many readers. But they are also subjective and imprecise. Accordingly, we turn to quantitative benchmarks.
4.2 Variation in the Data
A simple quantitative benchmark for assessing forecast uncertainty is the amount of variation in the data. This benchmark is useful for answering the question: How much does the forecast explain?
A simple measure of data variation is the standard deviation or variance of actual outcomes. This is explicit in some forecast comparisons (Campbell 2007; Vogel 2007; Edge and Gurkaynak 2011) and implicit in many more (as the denominator in the R2 of popular Mincer-Zarnowitz regressions). However, a conventional or ‘centred’ standard deviation measures differences from the sample mean. The sample mean is not available at the time of the forecast and does not represent an uninformative alternative. So comparisons with the standard deviation can set an unreasonably high standard; they do not really measure whether the forecast has explanatory power. A more interesting (though very similar) benchmark is the RMSE of an ‘uninformative’ or ‘null’ forecast such as an assumption of no change. A forecast that is more accurate than this uninformative alternative can be said to explain some of the variation in the data. We focus on uninformative alternatives that lend themselves to simple interpretations. A forecast that outperforms a random walk can be said to explain changes. A forecast that outperforms the historic mean can be said to explain the level.
Table 1 compares the RBA's forecast errors with those of uninformative alternatives. We show results at horizons 3 quarters and 7 quarters after the forecast, a cut of the data that avoids the duplication arising from overlapping 4-quarter changes but still summarises most of the sample. We describe these horizons as the first year and second year of forecasts, recognising that the current quarter is covered by the 3-quarter-ahead forecast. Appendix D shows comparisons at other horizons.
| Variable | Null alternative | Horizon | RMSE | Significance p-value | Uncentred R2 | ||
|---|---|---|---|---|---|---|---|
| RBA | Alternative | Ratio | |||||
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) |
| Underlying inflation; 4-quarter percentage change | Random walk | First year Second year | 0.54 0.80 |
0.73 1.08 |
0.74 0.74 |
.02 .15 |
0.46 0.46 |
| Underlying inflation; 4-quarter percentage change | Target | First year Second year | 0.54 0.80 |
0.74 0.78 |
0.72 1.03 |
.06 .87 |
0.48 −0.05 |
| CPI inflation; 4-quarter percentage change | Random walk | First year Second year | 0.89 1.27 |
1.90 2.19 |
0.47 0.58 |
.00 .03 |
0.78 0.67 |
| CPI inflation; 4-quarter percentage change | Target | First year Second year | 0.89 1.27 |
1.41 1.36 |
0.63 0.93 |
.04 .78 |
0.60 0.13 |
| GDP growth; 4-quarter percentage change | Historical mean | First year Second year | 1.44 1.39 |
1.28 1.39 |
1.13 1.00 |
.23 .94 |
−0.28 −0.01 |
| Unemployment rate; 4-quarter percentage change | Random walk | First year Second year | 0.62 0.97 |
0.67 0.89 |
0.92 1.10 |
.63 .69 |
0.15 −0.20 |
The top row of Table 1 shows that the RMSE for underlying inflation in the first year of the forecast horizon is 0.54 percentage points (column (4)). This can be compared with forecasts that inflation will remain at its rate over the preceding four quarters. This ‘no change’ or ‘random walk’ forecast has an RMSE of 0.73 percentage points (column (5)).[3] The RMSE of a random walk forecast equals the (uncentred) standard deviation of changes.[4] An RMSE ratio (column (6)) less than one – 0.74 in this case – indicates that the forecast is able to explain some of the variation in changes in underlying inflation. This may sound a trivial accomplishment, but it is one that foreign central banks have often not achieved. For example, Atkeson and Ohanian (2001) find that CPI forecasts of the US Federal Reserve are less accurate than a random walk. Variations on this result using other sample periods and measures of inflation are reported by Reifschneider and Tulip (2007), Tulip (2009) and Edge and Gurkaynak (2011). Similarly, Goodhart (2004, p13) reports that the Bank of England ‘does not appear to be able to provide any predictive guide at all to the fluctuations of output growth, or inflation, around its trend over a year in advance’.
The superior accuracy of the RBA forecast over the random walk is statistically significant, with a p-value of 2 per cent (column (7)). These p-values, constructed from Diebold-Mariano (1995) tests,[5] represent the chance that we might see the differences between the forecasts' mean squared errors if the forecasts were equally accurate.
A direct measure of the share of the variation in the data that is explained by the forecast is an uncentred R2 statistic (Hayashi 2000, p20), defined as
where: yt is the variable being forecast;
ft is its forecast; and
 is the uninformative forecast, which
can often be interpreted as the population
mean.[6]
Weather forecasters refer to this measure as a ‘skill score’ (Murphy
1988). An R2 of zero, meaning the forecast has no
explanatory power, occurs when the forecast is as accurate as the uninformative
alternative. When the alternative is a random walk, it is simple to think of
the variable being forecast as being in changes, with a mean of
zero.[7]
The MSE and (uncentred) Variance, represent the square of
the RMSEs shown in columns (4) and (5) respectively. The second line of Equation
(1) follows from the first by dividing both numerator and denominator on the
first line by n, the number of observations. The R2
estimate of 0.46 shown in row 1, column (8) of Table 1 indicates that the RBA's
forecasts account for about half the variance of changes in underlying inflation
over the first forecast year.
is the uninformative forecast, which
can often be interpreted as the population
mean.[6]
Weather forecasters refer to this measure as a ‘skill score’ (Murphy
1988). An R2 of zero, meaning the forecast has no
explanatory power, occurs when the forecast is as accurate as the uninformative
alternative. When the alternative is a random walk, it is simple to think of
the variable being forecast as being in changes, with a mean of
zero.[7]
The MSE and (uncentred) Variance, represent the square of
the RMSEs shown in columns (4) and (5) respectively. The second line of Equation
(1) follows from the first by dividing both numerator and denominator on the
first line by n, the number of observations. The R2
estimate of 0.46 shown in row 1, column (8) of Table 1 indicates that the RBA's
forecasts account for about half the variance of changes in underlying inflation
over the first forecast year.
Another benchmark is the midpoint of the RBA's target range for inflation, 2.5 per cent (henceforth, ‘the target’). Comparisons between the forecast and this benchmark are shown in the next part of Table 1. The R2 of 0.48 indicates that RBA first-year forecasts of underlying inflation account for about half the deviations of underlying inflation from the target. However, over the second forecast year, the ratio of RMSEs is about one and the R2 is about zero. So a forecast of 2.5 per cent was about as accurate a guide to underlying inflation as the second-year RBA forecast. This result is consistent with successful targeting of the inflation rate. At horizons over which monetary policy has a substantial influence, deviations of inflation from the target should generally be unpredictable. If there were predictable deviations, it would mean that the central bank was expecting that it would miss its target and was not acting to prevent this. See Edey and Stone (2004) for further discussion of forecast deviations of inflation from the target.
Results for CPI inflation are shown in the next two parts of the table. Again, forecasts have substantial explanatory power in both levels and changes. The first-year forecasts significantly outperform both a random walk and the target. One feature of the CPI estimates (which was less clear for underlying inflation) is that the target is more accurate than the random walk, reflecting rapid reversion of headline inflation to the mean. Reflecting this mean-reversion, the RBA's forecasts outperform a random walk more often than they beat the target. Put more simply, the forecasts can successfully predict changes in inflation, even when it is difficult to predict the level of inflation.
Two differences between the results for underlying inflation and the CPI are worth noting. First, as shown in column (4), forecast errors are considerably smaller for underlying inflation than for CPI inflation. That, of course, is one reason many economists like to focus on underlying inflation. We know more about it than we do about CPI inflation. The RBA has invested substantial resources in constructing measures of underlying inflation with higher signal/noise ratios (see Richards and Rosewall (2010) and references cited therein). The greater predictability of underlying inflation relative to the headline CPI is a reflection of that effort.
Second, the RBA's forecasts for headline inflation have had more explanatory power than those for underlying inflation, as measured by the R2 estimates in column (8). This largely reflects the spike in the CPI in 2000:Q3, due to the introduction of the Goods and Services Tax (GST), which was factored in to the CPI forecasts from 1999:Q1. See Figure 1, top right panel. The GST had minimal direct effect on the measure of underlying inflation used at the time, which was the weighted median excluding interest and taxes.
For GDP growth, our uninformative alternative forecast is the historic (since 1959) mean.[8] For the first-year GDP forecast, this alternative is more accurate than the RBA's forecast. That is, forecasts have less explanatory power than the mean. Reflecting this, the RMSE ratio is greater than one and the R2 is negative. For the second-year GDP forecast, the forecast is as accurate as the mean, so the R2 is zero.
Low and even negative forecast R2s are not unusual. They have been found by many researchers for many different kinds of macroeconomic forecasts. For example, Vogel (2007, Table 3) finds them for both Consensus Economics and OECD forecasts of GDP growth in the G7 economies. Atkeson and Ohanian (2001) implicitly find them for the US Federal Reserve's forecast of changes in the US CPI. Campbell (2007) finds them for the Survey of Professional Forecasters' forecasts of US GDP growth. Tulip (2009) finds them for Federal Reserve forecasts of US GDP growth and the GDP deflator. Goodhart (2004, Table 5) reports more dramatic results for the Bank of England's GDP forecasts (specifically outcomes are negatively correlated with forecasts).
That said, the low explanatory power of macroeconomic forecasts is a striking result, with important implications. For example, it affects how much weight should be placed upon forecasts of GDP in determining macroeconomic policy. More generally, it is relevant to debates as to whether policy should be ‘backward looking’ (as in some Taylor rules) or ‘forward looking’ (as in optimal control exercises).
Results for the unemployment rate are shown at the bottom of Table 1. We use the previous level as an alternative forecast, which is equivalent to examining whether unemployment forecasts outperform a random walk. The R2 can be interpreted as measuring how much of the variance of changes in the unemployment rate is explained by the forecast. Short-horizon unemployment forecasts seem to have some explanatory power, accounting for 15 per cent of changes in unemployment over the first year. But at longer horizons, the forecasts have been less accurate than a random walk.
To summarise the results in this section, the forecasts have substantial explanatory power for both the level and change in inflation over the next year, but – consistent with successful inflation targeting – at longer horizons deviations in underlying inflation from the RBA's target seem to be unpredictable. Uncertainty about the forecasts for GDP growth and (beyond the immediate horizon) changes in unemployment is about the same as the variation in these variables. In other words, forecasts for these variables lack explanatory power.
The ability to predict short-term variations in inflation but not in activity might be interpreted in different ways. One possibility is that the two variables are unrelated: the Phillips curve is flat. However, empirical evidence of many forms from many countries is inconsistent with that view. Another interpretation is that GDP growth is a poor measure of inflationary pressures, perhaps because it reflects changes in supply conditions or because it is the level of activity (relative to potential) that affects inflation, rather than the growth rate. Related to this, it may be that the RBA's implicit forecasts of the output gap usefully inform the inflation forecast; though this signal is difficult to discern after the event due to supply shocks. A third possibility is that influences on inflation other than demand are important. Whatever the explanation, the different explanatory power of forecasts for different variables has clearer implications for the presentation of the outlook. Specifically, we can talk more confidently about the near-term outlook for inflation than we can about the outlook for GDP growth. That emphasis is reflected in the SMP.
4.3 Uncertainty about Others' Forecasts
A benchmark that is especially relevant to improving forecast performance is the accuracy of other forecasters. To this end, we examine the output and inflation forecasts provided by Consensus Economics, a regular survey of about two dozen private sector forecasters. We use the average forecasts of 4-quarter changes in the CPI and real GDP, which we have on a quarterly basis since December 1994. We focus on these forecasts, rather than those of year-average changes which Consensus publishes more frequently, to facilitate comparisons with the forecasts published in the SMP. Consensus forecasts are proprietary, available via subscription at <www.consensuseconomics.com.> Summary statistics are reported here with permission.
As shown in Table 2, RBA forecasts for CPI inflation have been slightly more accurate than those of Consensus at all horizons. The differences are small and not statistically significant.
| Horizon | RMSE | Significance | ||
|---|---|---|---|---|
| (quarters ahead) | RBA | Consensus | Ratio | p-value |
| 0 | 0.27 | 0.31 | 0.86 | .15 |
| 1 | 0.49 | 0.50 | 0.97 | .74 |
| 2 | 0.71 | 0.71 | 0.99 | .93 |
| 3 | 0.87 | 0.93 | 0.94 | .48 |
| 4 | 1.07 | 1.14 | 0.94 | .37 |
| 5 | 1.20 | 1.31 | 0.92 | .21 |
| 6 | 1.21 | 1.35 | 0.90 | .15 |
| 7 | 1.22 | 1.24 | 0.99 | .90 |
As shown in Table 3, Consensus forecasts of GDP growth have been significantly more accurate than those of the RBA.
| Horizon | RMSE | Significance | ||
|---|---|---|---|---|
| (quarters ahead) | RBA | Consensus | Ratio | p-value |
| 0 | 0.80 | 0.78 | 1.03 | .65 |
| 1 | 1.12 | 1.00 | 1.12 | .03 |
| 2 | 1.28 | 1.16 | 1.11 | .04 |
| 3 | 1.37 | 1.24 | 1.11 | .02 |
| 4 | 1.33 | 1.22 | 1.10 | .02 |
| 5 | 1.33 | 1.19 | 1.11 | .07 |
| 6 | 1.35 | 1.18 | 1.14 | .03 |
| 7 | 1.34 | 1.21 | 1.11 | .08 |
There are several possible reasons for this result, though it is not clear that these fully account for the difference. For example, Consensus has a timing advantage for the last few years of the sample. Consensus conducts its survey in the last month of the quarter, after the publication of the national accounts. That is similar timing to RBA forecasts until 2008, after which its forecast for GDP was published in the middle month of the quarter. However, given that forecast accuracy does not vary much with the horizon (as can be seen in the table, and discussed further in Section 5.1), this advantage is not important other than for very short horizons. For horizons beyond one year, Consensus forecasts published the previous quarter outperform RBA forecasts by similar margins.
Another possible reason for the greater accuracy of Consensus is that their interest rate assumptions may be more realistic. As discussed in Appendix B, the RBA's GDP errors are significantly correlated with the slope of the yield curve at the time of the forecast, a measure of how much the market expects interest rates to change. However, estimates of this effect are small. When an estimate of the effect of the yield curve is removed from the RBA's GDP errors, the RMSE declines by 5 per cent at a 3-quarter-ahead horizon. This is still larger than the Consensus RMSE, though the difference is no longer statistically significant.[9]
The competitive (or ‘horse race’) aspect of these comparisons has curiosity value and is relevant to improvements in forecasting technique. For example, it implies the RBA might improve the accuracy of its GDP forecasts by placing greater weight on the Consensus average.[10] However, for our purposes, the similarity of the forecast errors may be more important than their differences. This is illustrated in Figure 4, which shows 3-quarter-ahead forecast errors for year-ended GDP growth for the RBA and Consensus. Differences between the errors are small relative to the variation in the data. At this 3-quarter-ahead horizon, the difference between the RMSE of the RBA (1.37 percentage points) and that of Consensus (1.24 percentage points) is statistically significant (p = .02). However this difference is not obviously significant in economic terms, being close to rounding error.
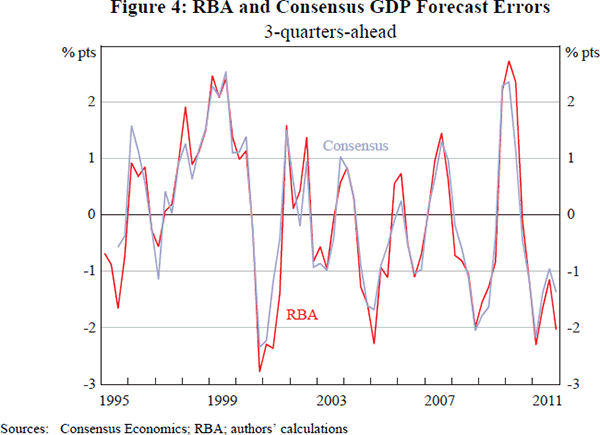
Overall, differences in forecast accuracy seem small, with relative performance varying across different variables. So, in qualitative terms, uncertainty about the Consensus forecast seems to be about the same as uncertainty about the RBA forecast. This similarity in accuracy is often found in comparisons of macroeconomic forecasters (for example, Reifschneider and Tulip (2007)). One implication of that similarity is that inferences about uncertainty around the RBA's forecast can (cautiously) be based on the track record of private sector forecasts and vice versa.
4.4 Disagreements and Revisions
It is common for forecasters to argue over a disagreement of say half a percentage point in their GDP forecasts. Revisions of similar size are often described as a substantial change in the outlook. As Stevens (2011) discusses, the magnitude of forecast errors provides useful context for assessing these differences. Some 22 per cent of the RBA's forecasts of GDP growth over the following four quarters were accurate to within half a percentage point. The results in Section 4.3 suggest that private sector errors would be similar. So, even if one forecast were the most likely outcome, the likelihood of an outcome closer to the alternative would be high. That is, one cannot have confidence that one forecast is correct and that a similar forecast is not. Put slightly differently, if the 90 per cent confidence interval for one forecast spans a range of 1 to 6 per cent while that of another (or previous) forecast spans a range of 2 to 7 per cent, those forecasts should be seen as being in substantial agreement.
That said, when the costs of policy mistakes are symmetric, then policy decisions should be made on the basis of the central tendency of forecasts. Then differences in the central tendency can have important implications and explanations of revisions and disagreements can be useful.
Footnotes
See Part VI, titled ‘Overconfidence’ in Kahneman, Slovic and Tversky (1982) or, for an accessible summary, the Wikipedia (2012) entry ‘Overconfidence Effect’. Contrary to what might be suspected, this bias is not easily overcome. Overconfidence is found among experts and among survey subjects who have been thoroughly warned about it. [2]
For consistency of comparisons, we only calculate errors for the alternative for those quarters for which there is a comparable forecast. [3]
An uncentred standard deviation, variance or R2 measures deviations about the population mean of zero instead of about the sample mean. In our context, centred and uncentred statistics have much the same interpretation and are empirically quite close. [4]
We regress the difference in the squared errors on a constant and report the p-value from a t-test of the hypothesis that the constant is zero. We use Newey and West's (1987, 1994) autocorrelation-robust standard errors, calculated with their suggested lag truncation, which typically is three quarters. The reliability of Newey-West variances is not clear, given the small size of our samples, the non-normality of squared errors, and the moving-average (MA) structure of our data. We explored alternatives that address some of these issues, specifically alternative bandwidth selection rules, West's (1997) MA-robust standard errors, and a block-bootstrap. But none of these approaches address all the features of our data. [5]
The R2 measure we present should not be confused with the R2 from a hypothetical ‘Mincer-Zarnowitz’ regression of actual outcomes on the forecast. Conceptually, this hypothetical R2 would equal ours if the coefficient on the forecast were constrained to equal one, the intercept was constrained to equal zero, and the dependent variable was measured as deviations from the uninformative alternative. Mincer-Zarnowitz regressions are popular. However, decision-makers need to form judgements about the explanatory power of the forecast, not the explanatory power of α + β Forecast, where α and β are parameters that are estimated after outcomes are known. [6]
The change in inflation, h quarters ahead, which is equal to the forecast error from the random walk forecast, is measured as πt + h − πt − 1, where πk is the percentage change in prices in the four quarters to k and t is the quarter in which the forecast is made. [7]
We measure the historic mean as average GDP growth from 1959 through to the quarter preceding the forecast, measured using real time data from Stone and Wardrop (2002), kindly updated for us by Tim Robinson. Similar data (more thoroughly documented) are now publicly available at the website of the Department of Economics at the University of Melbourne (<http://www.economics.unimelb.edu.au/RTAustralianMacroDatabase/Database% 20and%20Documentation.html>). [8]
Moreover, this comparison overstates the importance of differences in interest rate assumptions, given that we make no corresponding adjustment to Consensus and that the adjustment uses information after the event which was not available at the time of the forecasts. [9]
It is possible that individual members of the Consensus panel might also be able to improve their forecasts by moving toward the mean. Of course, were many members of Consensus to do this, the behaviour of the average would noticeably change, becoming subject to herd dynamics. [10]