RDP 2012-07: Estimates of Uncertainty around the RBA's Forecasts 5. Other Properties of the Confidence Intervals
November 2012 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 690KB
The confidence intervals presented in Figure 3 are a blend of data and assumptions. In particular, we estimate the width of our confidence intervals, at each horizon, based on the empirical record. However, we assume that some other properties of past historical errors are unlikely to apply in the future. Specifically, our intervals are unbiased and symmetric. Whether normality should also be assumed depends on the purpose. We discuss each of these assumptions in turn.
5.1 Effect of the Horizon
One might expect that the further events are in the future, the harder they are to forecast. That is, fan charts should fan out. This may seem to occur in Figures 2 and 3. However, much of the fanning in those charts is an artefact of data construction. Near-term forecasts for 4-quarter changes are made within the period being forecast and include ABS estimates for the first few quarters. It is not surprising that uncertainty widens as the event being forecast includes less of the known past. This effect is larger for forecasts of year-average changes. When this effect is removed, there is surprisingly little effect of the horizon on uncertainty about growth rates.
The effect of 4-quarter changes on increasing uncertainty can be removed by examining quarterly changes. Figure 5 shows RMSEs by horizon for forecasts of quarterly GDP growth. The dark line denotes RMSEs using the same sample of forecasts as used above, for example in the lower left panel of Figure 2. These estimates are essentially unaffected by the horizon. That is, we seem to know about as much (or as little) about GDP in the current quarter as we do about GDP growth two years ahead.
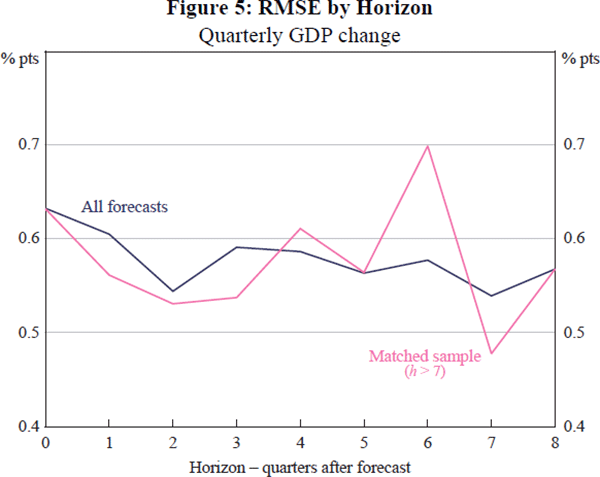
Another factor that distorts the effect of the horizon on uncertainty is changes in the sample. Because the forecast horizon has increased over time, our sample of long-horizon forecasts is smaller and more recent than our sample of short-horizon forecasts. So the GFC, for example, has a larger effect on our sample of long-horizon forecasts, than on our sample of short-horizon forecasts. To avoid differences like these affecting comparisons, we restrict the sample to the 24 forecasts in which the horizon extended at least 8 quarters ahead. The light line in Figure 5, labelled ‘h > 7’, shows RMSEs from this matched sample. The RMSEs shown by this line have the same initial conditions, with only the horizon changing. The matched sample estimates are more volatile. Still, uncertainty does not seem to increase with the horizon.
One implication of these results is that surprises to GDP growth are not persistent. That is, there is little inertia or momentum in the unpredictable component of GDP growth.[11] If there were substantial momentum, the surprises would accumulate and the fan chart would fan out.
Another implication is for comparisons between forecasts of GDP growth made at different times in a quarter. The absence of a substantial effect of the horizon on forecast errors means that one need not worry too much about the precise timing of forecasts or whether one forecast had an informational advantage over the other. Whether a forecast we record as being 3 quarters ahead is really 2 or 4 quarters ahead will make little difference to our results. Researchers in the United States (Romer and Romer 2000; Edge and Gurkaynak 2011) have precisely calculated the timing of economic forecasts relative to data releases and other forecasts. For analysis of Australian GDP forecasts, the precise timing of which does not seem to matter, that effort seems unlikely to be worthwhile.
Whether uncertainty about inflation increases with the horizon is harder to assess, given that much of our source data is in year-ended-change format. Internal RBA estimates suggest that current-quarter CPI forecasts benefit from high-frequency data on oil and food prices. Whether this advantage helps forecast inflation in following quarters is less clear. In Figures 2 and 3 the dispersion of inflation forecast errors widens with the horizon, even beyond a horizon of 3 quarters ahead. However, this ‘fanning’ could reflect changes in the sample: we have more forecasts with relatively short horizons and these forecasts could have been for periods when inflation did not behave unusually. That possibility is consistent with a matched sample of forecasts for year-ended underlying inflation for which the horizon extends at least 8 quarters, in which RMSEs are flat at horizons beyond 3 quarters. The limited data we have on quarterly underlying inflation also show a surprisingly small effect of the horizon on RMSEs, when initial conditions are held constant. However, given the small sample, these results are not strong.
For other variables, there is a stronger effect of the horizon. This is clearest for variables measured in levels, such as the unemployment rate or the level of GDP. Although surprises to growth rates are not persistent, those to levels are.
5.2 Bias
We have assumed that confidence intervals are centred on the forecast. An alternative assumption would be to centre the intervals on the forecast plus the mean or median error. Whether this matters depends on whether average errors have differed from zero. To assess this, we regress past forecast errors for each variable at each horizon on a constant. Results are reported in Table 4. The coefficient on the constant represents the average amount by which outcomes exceed forecasts. This is reported in the columns labelled ‘bias’. Whether this bias is large relative to the noise in the data can be gauged by t-tests for the hypothesis that the constant is zero. P-values for these tests, calculated using autocorrelation-robust standard errors, are also reported in the table.
| Horizon | Underlying inflation |
CPI inflation |
GDP growth |
Unemployment rate |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (quarters ahead) | Bias | p-value | Bias | p-value | Bias | p-value | Bias | p-value | |||
| 0 | −0.01 | .78 | −0.04 | .13 | 0.18 | .12 | −0.07 | .00 | |||
| 1 | −0.00 | .99 | −0.04 | .56 | 0.18 | .30 | −0.16 | .00 | |||
| 2 | −0.00 | .96 | −0.02 | .83 | 0.17 | .45 | −0.25 | .00 | |||
| 3 | −0.03 | .81 | −0.06 | .71 | 0.07 | .80 | −0.31 | .00 | |||
| 4 | −0.04 | .74 | −0.07 | .76 | −0.13 | .60 | −0.36 | .01 | |||
| 5 | −0.07 | .61 | −0.11 | .67 | −0.29 | .22 | −0.37 | .01 | |||
| 6 | −0.06 | .71 | −0.09 | .73 | −0.44 | .10 | −0.40 | .02 | |||
| 7 | −0.02 | .91 | −0.16 | .58 | −0.59 | .04 | −0.39 | .07 | |||
| 8 | 0.06 | .73 | 0.06 | .86 | −0.71 | .02 | −0.61 | .06 | |||
As can be seen in the left half of the table, bias in the inflation forecasts is approximately zero over this sample period. So centring confidence intervals for inflation on the forecast is in line with past experience. In contrast, GDP forecasts were too low at short horizons and too high at longer horizons, though the results are generally not significant. However, outcomes for the unemployment rate have, on average, been significantly below expectations. For example, the unemployment rate 3 quarters after the forecast averaged 0.3 percentage points below its prediction (p = 0.004). As can be seen in Figure 1 (third panel on right), the downtrend in unemployment was consistently underestimated during our sample period.[12]
A finding of ex post forecast bias is not unusual. It commonly occurs when there is a persistent shock to the economy that forecasters learn about gradually. For example, forecasters in many OECD countries persistently understated the rate of inflation in the 1960s and 1970s, then persistently overstated it in the 1980s and 1990s. Over the past decade, rising oil prices have repeatedly pushed headline inflation above expectations. Over the same period, Kearns and Lowe (2011, Figure 10) show that the RBA consistently underestimated the strength of the terms of trade.
However, it is doubtful whether the bias in these small samples is representative of the population. The errors may be random or systematic. If the latter, forecasters can be expected to learn and adjust their forecast. Neither case is likely to persist. So even when the errors do not have a zero mean (ex post, or after the event), we would still centre the confidence intervals about the forecast. That is, we assume past bias will not continue.
5.3 Symmetry
It is often suggested that the distribution about a particular forecast is skewed. For example, the November 2011 SMP described the risks to the central projection of global activity as skewed to the downside because of financial problems in the euro area. In practice, empirical estimates of skewness are difficult to interpret when the sample mean is not zero. Furthermore, they often reflect large outliers, which are observed infrequently. Neither small-sample bias nor outliers are a reliable guide to the future.
For simplicity, the confidence intervals in Figure 3 assume that errors are symmetric. We are not arguing that the distribution about future forecasts should be assumed to be symmetric. Rather, judgements about skewness are likely to be based on information other than the skewness in the historical data.
5.4 Normality
In Figure 3, we reported quantiles of the empirical distribution of forecast errors. A more common approach to estimating confidence intervals is to assume that errors follow a known distribution, the parameters of which can be estimated or imposed. In particular, many foreign central banks assume that the errors are normally distributed with a zero mean and a standard deviation equal to that of a sample of past errors (see Appendix A).
In practice, the two approaches provide similar estimates. This is shown in Figure 6, which compares RMSEs with the 68th percentile of the empirical distribution of absolute errors for our four variables. Were the errors distributed normally, these estimates would be equal. In practice, they differ slightly, with the differences typically being within rounding error.[13]
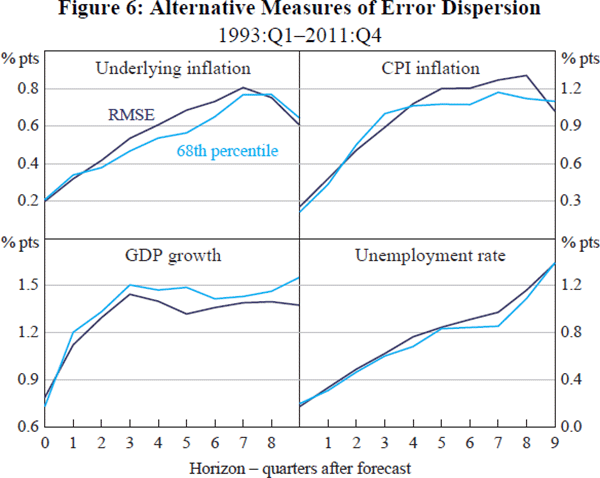
The similarity of the estimates in Figure 6 suggests that normality is a reasonable description of the data. To be more precise, a confidence interval equal to the forecast plus and minus one RMSE can realistically be described as approximately ‘a two-thirds confidence interval’. Whether normality is a reasonable description as one extends into the tails is harder to assess. In a sample of 19 years, we have very few ‘once-in-a-generation’ surprises. However, the experience of other countries, noted below, suggests that large surprises may be more frequent than implied by a normal distribution. Haldane (2012) argues that macroeconomic surprises often have fat tails.
As a measure of dispersion, quantiles and RMSEs have different advantages. If the purpose is to construct confidence intervals (especially other than two-thirds), then quantiles are simple, direct and do not require a questionable assumption about normality. However, for a summary measure of uncertainty or forecast comparisons, RMSEs are more comprehensive, with useful statistical properties. For example, they map into analysis of variance, they are easily scaleable, and they have less sampling variability: in small samples, RMSEs jump around less unpredictably than quantiles.[14]
Footnotes
Results in Section 4.2 suggest that virtually all variations in GDP growth are unpredictable. So there is little momentum in total GDP growth. [11]
Three observations might be interesting to note. First, the bias in the unemployment forecasts was accompanied by zero bias in underlying inflation. This suggests that the bias in the unemployment forecasts was offset by similar bias in the NAIRU and/or unanticipated appreciation of the exchange rate. Second, although unemployment fell over the sample, it is stationary over long time periods. It may be that unemployment would be systematically underpredicted when it trends upward. If so, the problem would be persistence in errors, rather than bias. Third, much (though not all) of the bias reflects predictions of rising unemployment at times of the Asian financial crisis, the global slowdown of the early 2000s and the global financial crisis that did not come to pass. [12]
Alternative approaches to this issue include a Jarque-Bera test or comparing histograms with a normal distribution. These alternatives test for normality at places in the distribution, such as near the centre, which are less interesting for the purpose of constructing confidence intervals. A Jarque-Bera test (which would need to be adjusted for serial correlation, presumably by Monte Carlo) gauges statistical significance, whereas Figure 6 indicates the magnitude (or ‘economic significance’) of departures from normality. [13]
For example, we construct 100,000 Monte Carlo simulations of artificial data with similar ARMA properties to our 3-quarter-ahead underlying inflation errors. The mean RMSE and 68th percentile (precisely, the 0.6827 quantile)are both 0.5 percentage points. The standard deviation of the RMSE is 0.070 percentage points, while that of the 68th percentile is 0.085 percentage points, about one-fifth larger. [14]