RDP 7901: Estimation and Statistical Evaluation of an Economic Model 5. Estimation Issues
July 1979
5.1 Averaging of data
Two stages of data averaging are used in estimation of the RBA76 model.[35] In the first stage, mid-period values' are obtained for the stock variables, to correspond with the measurement of the flow variables over the period. The second stage relates to the discrete approximation to the continuous time model, as defined by Wymer (1976). Whereas the usual discrete time model has a lagged dependent variable, the RBA76 model uses an average of the current and lagged value of the dependent variable. The exogenous variables (both stock and flow variables) are also averaged before estimation. This is an attempt to represent more accurately the information used by agents in their decision making.
The first averaging is less controversial than the second because it can be interpreted as lining up the data as well as part of the discrete approximation process, and in this section the effect of the second averaging is examined by re-estimating the base model without it. The parameter estimates are given in Table 3. The parameters representing adjustment speeds (ɑ1 to ɑ19) are in general smaller for the unaveraged model than the base model. The estimated parameters for monetary disequilibrium are smaller in value, and the parameters for this effect in the expenditure, labour demand and bonds equations are positive, although insignificant. Of the other four changes in sign of parameter estimates relative to the base model, only one is a significant by the “t-ratio” test: this is the parameter on the world interest rate in the demand for money which estimates with a large positive value.
The goodness of fit at the estimation stage is generally better for the unaveraged model: the main exceptions are the equations for exports, output, inventories and the exchange rate.
The amount of significant non-contemporaneous serial correlation in the unaveraged model, as indicated by the cross-correlation coefficient, has decreased slightly relative to the base model: this now occurs at lag 1 in fourteen equations rather than fifteen and at lag 2 in two equations rather than four.[36]
The conclusion that can be drawn from these results is that when the RBA76 model is estimated without the second stage averaging, the parameter estimates are in some cases different (and less plausible) from those of the model estimated with both data averaging stages. In interpreting this result, it should be noted that the specification of the base model has been influenced by estimation with both averaging stages, and thus this may be a biased test of the effect of data averaging. However, from the similarity of the serial correlation properties of the unaveraged model and the base model, it appears that the prewhitening filter applied to the data after the second data averaging stage (illustrated by the base model results) counteracts the serial correlation introduced by the discretisation of the continuous time model, although the residuals of the model before transformation exhibit significant serial correlation. This supports the results on the prewhitening filter reported in section 5.3.
| FIML | FIML | OLS | OLS | OLS | |
|---|---|---|---|---|---|
| Averaged | Unaverased | Linear Unaveraged | Non-linear Unaveraffed | Non-linear Averaged | |
| β1 | 1.0* | * | * | * | * |
| β2 | −.965 | −1.599 | −.411 | −.133 | .021 |
| β3 | −3.8* | * | * | * | * |
| β4 | −.716 | 3.620 | −.716* | −.716* | −.716* |
| β5 | −.01* | * | −.01* | −.01* | −.01* |
| β6 | .077 | .182 | .077* | .077* | .077* |
| β7 | .30* | * | * | * | * |
| β8 | −.146 | −.228 | −.061 | −.069 | −.077 |
| β9 | .016 | .018 | .014 | .026 | .036 |
| β10 | .010 | .012 | .016 | .001 | .016 |
| β11 | −.516 | −.050 | −.041 | −.041 | −.062 |
| β12 | .732 | .136 | .075 | .075 | .071 |
| β13 | −.470 | −.990 | −.480 | −.480 | −.436 |
| β14 | .5* | * | * | * | * |
| β15 | 2.273 | 1.096 | .504 | .139 | .079 |
| β16 | .031 | .014 | .037 | .014 | .004 |
| β17 | −.719 | −.722 | −.719* | −.719* | −.719* |
| β18 | .203 | .114 | .203* | .203* | .203* |
| β20 | .1* | * | * | * | * |
| β21 | .842 | .930 | .996 | .996 | 1.084 |
| β22 | .179 | .214 | .179 | .179 | .180 |
| β24 | 1.341 | .984 | .856 | .856 | .925 |
| β25 | .318 | .275 | .260 | .260 | .257 |
| β26 | .417 | −12.11 | .241 | .241 | .197 |
| β27 | −.047 | −.059 | −.125 | −.125 | −.141 |
| β28 | 12.791 | 15.53 | 12.67 | 12.67 | 13.13 |
| β29 | −.2* | * | −.105 | −.105 | −.228 |
| β30 | 1.828 | 2.058 | 1.505 | 1.505 | 1.694 |
| β31 | −.01* | * | * | * | * |
| β32 | .16* | * | * | * | * |
| β33 | 10.439 | 7.984 | 71.7 | 71.7 | 53.4 |
| β34 | −.622 | −.664 | −7.19 | −7.19 | −5.42 |
| β35 | 2.279 | 2.181 | 11.56 | 11.56 | 8.47 |
| β36 | .151 | .123 | .077 | .077 | .074 |
| β37 | −.030 | −.038 | −.020 | −.020 | −.021 |
| β38 | .028 | .028 | .025 | .025 | .022 |
| β39 | −9.605 | −29.575 | −13.85 | −13.85 | −7.87 |
| β40 | 4.915 | −6.255 | −8.71 | −8.71 | −1.49 |
| β41 | 1.084 | 1.123 | 1.085 | 1.085 | 1.219 |
| β42 | .008 | .004 | .005 | .005 | .009 |
| β43 | .054 | .078 | .025 | .025 | .032 |
| β44 | −.003 | −.003 | −.001 | −.001 | −.003 |
| β45 | −.010 | −.018 | −.008 | −.008 | −.009 |
| β46 | .100 | .041 | .083 | .083 | .106 |
| β47 | .058 | .009 | .040 | .040 | .085 |
| β48 | −.264 | −.528 | −.122 | −.122 | .069 |
| β49 | −.008 | −.023 | −.010 | −.010 | .001 |
| β50 | −.046 | .009 | .003 | .003 | −.008 |
5.2 OLS Estimation
The equations in the base model have been estimated with Ordinary Least Squares. As there is a lagged dependent variable in each equation, the “single equation” model is a discrete time model rather than a discrete approximation to the continuous model. In its treatment of lags, this is similar to the model used in section 5.1.[37]
The model was estimated first in an unconstrained form with no cross-equation restrictions imposed. However, where a parameter is in an equation on more than one variable, it was necessary to enter these variables as one composite variable to obtain a unique estimate of the parameter. The unconstrained OLS estimates for the equations specified in the model with cross equation restrictions are given in Attachment C. In some cases it was only possible to obtain the estimate of a combination of parameters.
With the exception of the parameter on the monetary disequilibrium term in the bonds equation, each of the monetary disequilibrium parameters estimates as a negative value although only the parameter in the price equation is significant.[38] The estimates of the parameters in desired money vary in magnitude and on occasions in sign between the equations. In particular, the estimates of the parameters on the world interest rate in the prices equation and the bond rate in the labour demand equation are positive, which is contrary to the expected sign and to the sign of the parameter estimates from the other equations. The two parameters in desired imports and output estimate close to the FIML discrete approximation values in the imports equation, but the parameter on the exogenous component of exchange rate expectations estimates as a small positive value in the output equation.
The parameter estimates for the model with parameters of the cross equation restrictions set at their FIML values are given in Table 3, with both linear and non-linear OLS estimates given for the six non-linear stochastic equations. The estimates for the linear and non-linear form of these equations are quite similar, with the exception of: the parameter on monetary disequilibrium in the expenditure equation which is positive and insignificant in the non-linear version, and negative and insignificant in the linear version; and the parameter on inventory disequilibrium in the imports equation which is larger in magnitude and significant in the linear version.
By way of comparison the parameter estimates for the model estimated with FIML are given in Table 3 along with the OLS estimates. They are represented diagrammatically in Figure 3, with the points on the chart indicating the percentage deviation of the OLS estimate from the FIML estimate. The two standard error range around the FIML estimate is also indicated. The estimates of adjustment speeds in the OLS model are generally lower than for the model estimated by FIML.[39]
Parameter Estimates of OLS Model relative to FIML estimates
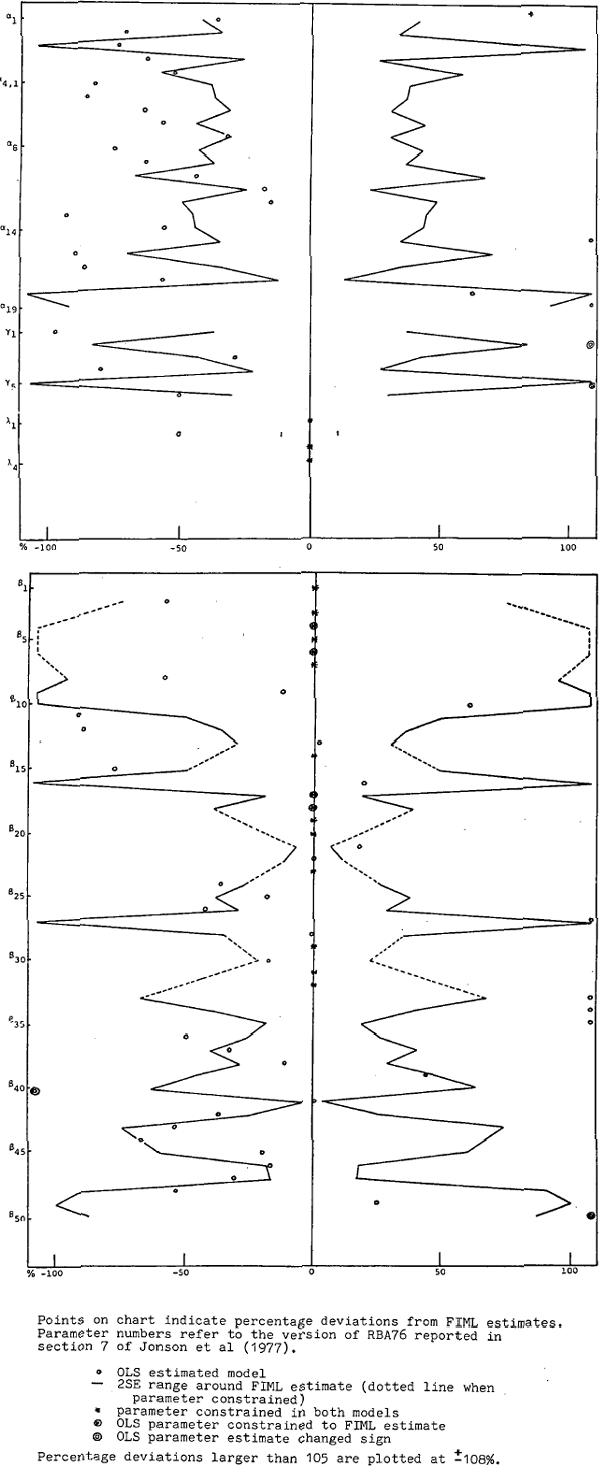
The estimated parameter on monetary disequilibrium is significant only in the price equation, and is positive in the equations for bonds and changes in labour demand. The estimated growth rate λ2 has a value of .009; the value estimated with FIML is .018. Other parameter estimates of note are the negative OLS estimate for the parameter on world interest rates in desired advances and the large parameters for desired capital inflow (these relate to the small estimated value for the adjustment speed in this equation). In general it can be said that the OLS model estimates replicate most results of the model estimated by FIML but cannot reproduce results such as monetary disequilibrium effects.
The full system control simulation paths of the linear and non-linear OLS models are broadly similar; the notable differences being a better tracking performance for the imports, output and capital flows equations in the linear version, and better performance for the advances, taxes, money, price and wage equations in the non-linear version. For the price and wage equations, however, the tracking performance is poor in both versions.
When a government expenditure shock is applied to the OLS model, the simulation stops in 1971(2) with negative reserves: in the control simulation, predicted reserves is below the actual value at that time but subsequently rises. Up until 1971(2) prices and wages with the government expenditure shock are higher than in the control solution, as are bonds, capital flows, taxes and the bond rate.
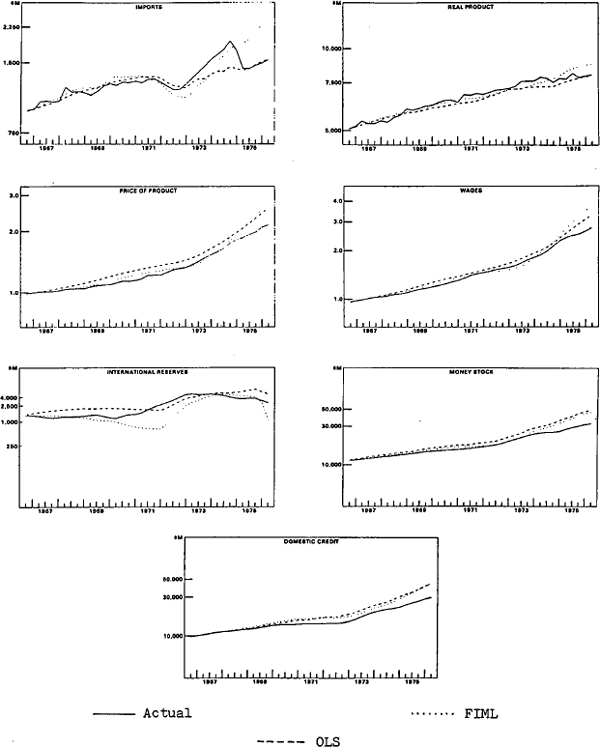
Root mean square percentage errors from control simulation of the OLS and FIML models are reported in Table 4 for the periods 1959(3)–1975(4) and 1966(3)–1976(1).[40] The OLS and FIML control simulation paths of key variables in the model for the period 1966(3)–1976(1) are shown in Figure 4, along with the actual data series for these variables. For the period 1966(3)–1976(1) the RMSPE for the OLS model are generally smaller than those for the FIML model. The simulation paths for imports and prices are above the actual values by a larger amount for the FIML model than the OLS model, while money overpredicts for the whole period with the OLS. model. The bond rate is underpredicted with the OLS model and overpredicted with the FIML model.
Over the period 1959(3)–1975(4), prices and wages are overpredicted with the OLS model, as are money and domestic credit, while prices and wages are underpredicted with the FIML model. The tracking performance for the bond rate is poor in both cases, with the OLS model overpredicting and the FIML model underpredicting the actual values.
Averaging of the data for OLS
Parameter estimates for the OLS model with second stage data averaging are given in Table 4: this represents a discrete approximation to a continuous time model. Of the 23 adjustment speed estimates, 15 are higher for the averaged OLS model than for the unaveraged OLS model, 7 are lower and one (the adjustment speed for indirect taxes) is negative. The parameters on monetary disequilibrium are similar in both models, with the exception of the parameter on the term in the bonds equation which is positive in the unaveraged model and negative in the averaged model. Other changes in sign of parameter estimates relative to the unaveraged model are the bond rate in desired expenditure and three terms in the exchange rate equation. The control simulation of the OLS averaged model is poor, with prices rising from early in the period. This sends most of the other variables off track. The simulation fails when reserves fall to zero in 1970(4).
| 1966(3)–1976(1) | 1959(3)–1975(4) | ||||
|---|---|---|---|---|---|
| FIML | OLS | FIML | OLS | ||
| 1 | 5.52 | 3.27 | 6.81 | 6.85 | |
| *2 | .21 | .21 | .27 | .26 | |
| 3 | 5.24 | 4.51 | 7.82 | 7.55 | |
| 4 | 15.39 | 9.20 | 16.05 | 10.49 | |
| 5 | 3.74 | 3.81 | 5.75 | 7.29 | |
| 6 | 7.15 | 8.72 | 10.47 | 18.88 | |
| 7 | 6.72 | 6.72 | 9.22 | 13.39 | |
| 8 | 11.11 | 7.90 | 6.80 | 10.82 | |
| 9 | 9.27 | 6.60 | 9.47 | 14.06 | |
| 10 | .60 | 2.51 | 1.02 | 2.28 | |
| *11 | .50 | .49 | .52 | .52 | |
| 12 | 7.74 | 7.06 | 10.86 | 11.68 | |
| 13 | 13.09 | 9.55 | 18.82 | 26.84 | |
| 14 | 12.99 | 11.16 | 15.06 | 14.18 | |
| 15 | 5.80 | 8.10 | 9.49 | 14.83 | |
| 16 | 7.18 | 5.14 | 9.51 | 11.60 | |
| 17 | 55.39 | 34.70 | 47.97 | 42.19 | |
| 18 | 12.23 | 17.21 | 7.48 | 21.96 | |
| 19 | 8.89 | 9.63 | 19.97 | 10.13 | |
| *20 | .68 | .52 | 2.44 | .93 | |
| 21 | 11.06 | 8.31 | 6.86 | 11.84 | |
| 22 | 5.64 | 3.23 | 18.76 | 9.76 | |
| 23 | 15.85 | 17.75 | 6.82 | 24.93 | |
| 24 | 1.47 | 3.70 | 3.00 | 5.77 | |
| 25 | 1.20 | 3.73 | 1.50 | 3.10 | |
|
* In these cases, the root mean square error is reported. |
|||||
Actutal and Control Solution Values FIML and OLS
The parameter estimates of the unaveraged OLS model and the unaveraged FIML model can also be compared from Table 3. With the exception of the monetary disequilibrium terms, the two sets of estimates are broadly similar.
The conclusions that can be drawn from this section are: parameter estimates of an unconstrained OLS model are not satisfactory; the parameter estimates and simulation properties of the linear and non-linear OLS model are similar; and, although the parameter estimates of the averaged OLS model are not very different from those of the unaveraged OLS model, the simulation performance of the averaged OLS model is considerably worse. In general, the OLS model estimates capture the core results of the model estimated by FIML but not some of the special results such as those represented by cross equation restrictions. The simulation performance of the two models is comparable, with the tracking performance of some equations better with FIML rather than OLS, and vice versa for other equations. Overall the simulation performance of the OLS model is slightly better than that for the FIML model, as indicated by the RMSPE. However, the problem with this type of comparison of a model estimated by OLS and FIML when the model has been specified with the FIML estimation technique is that unless the specification of the model is altered in light of the OLS results, the OLS model will have some unacceptable parameter estimates and thus the comparison with the FIML model could be regarded as biased. On the other hand, if the model estimated with OLS were to be re-specified, and this re-specification included adding extra equations, the model estimated with FIML would be at a disadvantage since the constraint imposed on the size of the FIML model by computing requirements is likely to cause some specification errors.
5.3 The Prewhitening Filter
Since the discretisation of a continuous time model with white noise residuals puts serial correlation into the residuals, the discrete time model is pre-whitened by filtering. all variables by the Continuous Systems Moving Average transformation (COSMA), following Wymer (1976). Bacon and Johnston (1977) compare the autocorrelation functions of the mid-77 version of RBA76 estimated with COSMA'd and non-COSMA'd data and find them to be similar, and thus conclude that the prewhitening filter is having little impact on serial correlation in the residuals. However, the relevant comparisons were made with residuals of the reduced form model: in this section, a comparison of structural residuals of a late-77 version of RBA76 estimated with both COSMA'd and non-COSMA'd data is reported.
The parameter estimates of the non-COSMA'd model are all the same sign as in the base model, although some of the parameter estimates have changed in magnitude. In particular, the adjustment speeds for changes in investment, changes in labour, exports and output have fallen in value, while the effect of the bond rate in desired consumption has become more negative, and the estimated parameter on the relative price term in desired money has increased in value and become significant. The goodness of fit in estimation, as measured by the coefficients of determination, are similar for both models, as are the eigenvalues, but the RMSPE in dynamic control simulation of the non-COSMA'd model (reported in Attachment B) are in general slightly higher than the base model. The number of cases of significant non-contemporaneous serial correlation in the structural residuals within and across equations at a given lag is reported in Table 5.
| Lag | Non-Cosma'd Model | Base Model | ||||
|---|---|---|---|---|---|---|
| Within Equation | Across Equation | Within Equation | Across Equation | |||
| Positive lag | Negative lag | Positive lag | Negative lag | |||
| 1 | 16 | 62 | 50 | 15 | 42 | 38 |
| 2 | 3 | 34 | 31 | 4 | 20 | 24 |
| 3 | 0 | 21 | 23 | 0 | 16 | 21 |
| 4 | 4 | 18 | 20 | 4 | 15 | 16 |
| 5 | 0 | 10 | 13 | 0 | 11 | 10 |
| 6 | 2 | 4 | 5 | 2 | 4 | 8 |
| 7 | 1 | 7 | 17 | 0 | 3 | 13 |
| 8 | 0 | 7 | 12 | 0 | 5 | 6 |
The non-COSMA'd model has a similar number of cases of significant within-equation serial correlation[41], but the values of the correlation coefficients are in general higher than those for the base model. The amount of cross-equation serial correlation is higher in the non-COSMA'd model than in the base model. These results indicate that serial correlation in the structural residuals is reduced by the COSMA transformation, but that a considerable amount of serial correlation is still present in the COSMA'd model.
5.4 The Shape of the Likelihood Surface
Two types of experiments were carried out to obtain more information on the shape of the likelihood surface for the particular version of RBA76 used in this study. The first was to permit the algorithm to operate with the default tolerance value (0.001) for the FIML estimation program: this implies that the algorithm will converge when the maximum proportional change in all of the parameters is less than 0.1%. The version of RBA76 reported in this paper as the base model was originally estimated with a tolerance of 0.5, which resulted in a set of estimates with a likelihood value of 7,370.51. After 15 iterations of this model, the maximum proportional change in all parameters was 0.023, and the likelihood value 7,376.69. With a further 17 iterations, the likelihood value remained the same, with the maximum proportional change falling to 0.0009. The set of estimates corresponding to the 32nd iteration had changed very little from the set after the 15th iteration, indicating that the maximum value of the likelihood function was closely approximated. From Table 6, the sign and significance of the parameter estimates obtained after 32 iterations with the default tolerance are mostly within 25% of those of the base model. A conclusion that can be drawn from this experiment is that for a model of the size of RBA76, which has 69 parameters, a tolerance value of about 0.03 or 3% may be the tightest convergence tolerance which is needed.
The second experiment used different sets of initial values for the parameters. One set gave an initial value of 0.05 to every parameter: in this case, two of the parameters (on the relative price term in desired money and desired bonds) converged to values that were unacceptably large and incorrectly negative. Three closely related parameters (γ1, γ2 and γ4) also did not estimate as acceptable values, which is not surprising given the unacceptable estimate of the relative price term in desired money. Only two other parameter estimates[42] took on values of the opposite sign to that in the base model. This result indicates that if only one or two important parameters, such as the relative price term in desired money, move to values in the wrong direction at the first iteration, some closely related parameters will also tend to unacceptable values, and the algorithm may not be able to reverse the direction of movement along the likelihood surface. The likelihood value of this set of estimates is 7,319.4, which is less than that for the base model, and the RMSPE from dynamic control simulation of this model are higher than those of the base model.
| Parameter change | Number of Parameters | ||
|---|---|---|---|
| 32-iteration model relative to base model | Initial ±0.1 relative to 32-iteration model | Initial 0.05 relative to 32-iteration model | |
| −10% to + 10% | 31 | 66 | 14 |
| ±10% to ±25% | 21 | 2 | 18 |
| ±25% to ±50% | 6 | 1 | 18 |
| more than 50% | 11 | 0 | 12 |
| sign change | 0 | 0 | 7 |
| total | 69 | 69 | 69 |
| became significant | 2 | 0 | 1 |
| became insignificant | 3 | 0 | 16 |
The other set of initial values gave a value of ±0.1 to the parameter, depending on the expected sign of the parameter. This produced a set of estimates in which as shown in Table 6, almost all parameters are within 10 per cent of those in the 32-iteration model.[43] The likelihood value for this set of estimates was 0.04 less than that for the 32-iteration model at 7376.65, with a maximum proportional change of .0272; and the dynamic control simulation of this model and the 32-iteration model are almost identical. Therefore, for this version of RBA76, the estimated model obtained when initial parameter values are set ±0.1 (depending on the expected sign of the parameter) is the same as the estimated model obtained when the initial parameter values are set according to expected sign and size.
Footnotes
For a discussion of discretisation and data averaging, see Bacon and Johnston (1977). [35]
The equations of the base model in which significant serial correlation occur were given in Table 2 in the previous section. For the unaveraged model at lag 1 significant serial correlation now occurs in equations 5, 20 and 21 but not in 1, 3, 19 and 23; at lag 2 in equation 23 but not in equations 2, 20 and 21. [36]
Mid-period stock values are used in the OLS estimation: this corresponds to the first data averaging stage. [37]
This is a similar result to that reported by Bacon and Johnston (1977) for the mid-1977 version of the model. [38]
It should be noted that since the OLS model is a discrete time model and the FIML model a discrete approximation to a continuous time model, a direct comparison of adjustment speeds may not be appropriate. [39]
Perazzelli (1977) compares full dynamic simulation of a linearised version of the mid-77 RBA76 model with simulations of the linearised model using constrained single equation estimates (in which cross equation parameters are set to their FIML estimates). The two sets of simulations are similar, with the constrained single equation set tending to track more of the short term [40]
Compared to the base model, the non-COSMA'd model has significant serial correlation at lag 1 in the equations for the bond rate and for changes in labour demand but not in the domestic credit equation; at lag 2 in the inventory equation but not in the equations for the bond rate and for changes in investment; at lag 7 in the direct taxes equation. [41]
The term Dlog R in the exchange rate and bond rate equations. Of the seven incorrectly signed parameter estimates, only one (Dlog R in the bond rate equation) was significant as indicated by the “t-ratio”. [42]
Of the 69 parameters, 63 parameter estimates were within 5%, and 48 within 1% of the estimates of the default tolerance model. [43]