RDP 7901: Estimation and Statistical Evaluation of an Economic Model 4. Linearisation Issues
July 1979
Since recent data has been more variable than much of that used for early model building, it is increasingly important that at least some relationships in a model be specified in non-linear terms. Some indication should be obtained of the degree of non-linearity in the model, and the order of magnitude of errors that are introduced if the model is linearised. If the model contains severe non-linearities, a suitable non-linear estimator may be required as it may not always be possible to approximate the relevant relationships closely by linear ones. Furthermore, the patterns of dynamic behaviour of a linearised model may be quite different from that of the non-linear model.
The non-linearities in the specification of a version of the RBA76 model are set out in Attachment A. These fall into two categories: identities, and individual terms in stochastic equations. As a result of initial work to code the non-linear model, several of the terms that had required linearisation were re-specified in a way which eliminated the need to linearise for estimation: the terms log (1+t3) and log (1−t1), rather than log t3 and log t1, were entered as variables; log (PxX−EPii) in the equation for capital flows was specified as two separate log terms; and log (G−T+DR) in the equation for government bonds was replaced by a monetary disequilibrium term (as in Jonson, Evans and Moore (1978)). These changes result in an estimated benchmark model with similar parameter estimates and properties to Model II.
4.1 Alternative linearisations
Since full-system non-linear estimation of the RBA76 model is not feasible at present, the model is linearised with a Taylor series expansion about a given point.[24] If the system has a steady state and if variables have changed substantially during the sample period, linearisation about the steady state may be most appropriate. For a shorter sample period where, although the variables have not deviated greatly from the sample means, the data observations may not be close to the steady state path, the model could be linearised about the sample means of the variables, as for example in Bergstrom and Wymer (1976) and Knight and Wymer (1978). It should be noted, however, that it is necessary to transform a model linearised about sample means in order to obtain information on the dynamic properties of the system and its capacity to produce plausible long run behaviour.
The RBA76 model has been linearised about a hypothetical steady state. Ideally, the steady state values should be obtained by solving the model, but since this has to date not been possible for RBA76, steady state levels are calculated on the assumption that 1958/59 represents a year when the economy was on the steady state growth path.
An alternative linearisation procedure is discussed in Walters (1978). From regression of each variable on a constant and time trend, two sets of linearisation constants are obtained: one set corresponds to the start of the observation period[25] (“star” values) and the other set to the midpoint of the period (“prime” values). After some experimentation with inclusion of an estimated time trend, Walters (1978) concludes that the time trend from the first order Taylor series approximation can be omitted. The argument for using the midpoint of the sample is that this value would seem to be a better approximation to the exponential growth path than the beginning of the period value, and could minimise the effect of divergent growth rates of variables within a linearisation. This procedure could therefore be regarded as an ad hoc alternative to linearisation about sample means.
The estimated models obtained using sets of linearisation constants calculated in this manner are compared with the benchmark model by examining sign and size of parameter estimates, control simulation RMSPE, residual serial correlation, measures of goodness of fit and eigensystem analysis. Model A refers to the model using “star” constants and Model B to the model using “prime” constants.
Two parameter estimates (the relative price term in demand for money, and inventory disequilibrium in the output equation) changed sign in Model B, but both estimates were insignificant according to the “t-ratio”. Table 1 gives an indication of the changes in size of the parameters of models A and B relative to the benchmark model. The estimated parameters of Model A are closer to the estimates of the base model than are the estimates of Model B, and several more parameters in Model B became insignificant as indicated by the “t-ratio”.
| Parameter change | Number of Parameters | |
|---|---|---|
| Model A | Model B | |
| −10% to +10% | 26 | 18 |
| ±10% to ±25% | 22 | 25 |
| +25% to +50% | 14 | 10 |
| more than 50% | 7 | 14 |
| sign change | 0 | 2 |
| total | 69 | 69 |
| became significant | 3 | 3 |
| became insignificant | 4 | 8 |
The goodness of fit measures compared are the coefficient of determination and the squared correlation coefficient of the estimated structural model.[26] For both Model A and Model B, these are similar to those of the base model, with the exception of a better fit for the output and inventory equations in Model B, and poorer fit for the capital inflow and foreign reserves equations in Model A.
The root mean square percentage errors of control simulation of the three models are reported in Attachment B. The errors are generally higher for Model A than for the base model (particularly for the equations for bonds, capital inflow, inventories and the exchange rate), while the simulation errors for Model B are larger than for the other two models, particularly for the equations for bonds, advances, money and domestic credit. This change in the dynamic properties of Model B is also evident from the eigenvalues of the models. While the base model and Model A both have one real positive eigenvalue, Model B has, in addition, a complex eigenvalue with a small positive real part, indicating the presence of an unstable cycle.
The procedure used to measure the degree of non-contem-poraneous serial correlation within the structural equations is the cross-correlation coefficient (Trevor (1978)). The equations with significant serial correlation at lag n as indicated by this measure are reported in Table 2. In general, the serial correlation present in Model B is similar to that in the base model, while the significant serial correlation present in Model A has increased. In particular, significant serial correlation at lag 3 is now present in the inventory and price of exports equations, and 4th-order serial correlation has been introduced into the equation for changes in investment. However, the bonds equation no longer exhibits significant 6th-order serial correlation.
| Base Model | Model A | Model B | |
|---|---|---|---|
| Lag 1 | 1 3 4 9 10 12 13 14 15 16 17 18 19 22 23 | 1 3 4 7 9 10 11 12 13 14 15 16 17 18 19 20 22 23 | 1 3 4 7 9 10 12 13 14 15 16 17 18 19 22 23 |
| Lag 2 | 2 7 20 21 | 2 7 21 17 | 2 7 12 21 |
| Lag 3 | 8 19 | ||
| Lag 4 | 6 7 22 23 | 2 6 7 22 23 | 6 7 22 23 |
| Lag 6 | 12 20 | 20 | 12 20 |
The conclusion that can be drawn from the comparison of these models is that the use of a different set of linearisation constants does alter some properties of the estimated model. The estimated parameters and dynamic properties of Model A, using constants calculated at the beginning of the period, are quite similar to the base model, although the degree of significant serial correlation present has increased. For Model B, which uses constants calculated at the mid-point of the period, the degree of serial correlation is similar to that in the base model: however, the parameter estimates and dynamic properties differ from those of the base model. These results illustrate the conflict which can arise when several different criteria are used to evaluate an econometric model. One conclusion, however, that the results do suggest is that the serial correlation evident in the base model is not removed by the use of these different sets of linearisation constants.
4.2 Non-linear simulation
The non-linearities in the specification of RBA76 have been coded for non-linear simulation.[27] The non-linear simulations are carried out with data that has not been prewhitened, since the prewhitening filter is appropriate at the estimation stage. Jonson et al (1977) report linear simulations on filtered data, but linear simulations on filtered and unfiltered data are found to be very similar.
The non-linearities were coded for simulation in stages, and in general at each stage the simulation tracking performance was slightly worse. This is not surprising in view of the fact that the estimated parameters had been optimised on simulation performance of a linearised version of the model. With regard to the four identities that had been linearised, the identity which altered the tracking performance to the greatest degree was that for domestic credit, suggesting that this could be an important source of non-linearity.
In coding individual non-linear terms in stochastic equations, it is necessary to obtain the non-linear equation constants. These can be calculated by subtracting the constants of the linearisation approximation from the estimated constants, although it was found that some of these derived equation constants had to be adjusted to ensure small simulation errors in the first period. Alternatively, non-linear equation constants can be obtained as the mean of residuals of the non-linear model over the estimation period: this is more appropriate than the first method since it does not involve the remainder term of the Taylor's series linearisation approximation, which may have a non-zero mean.
Linear control simulation and non-linear control simulation paths, along with the actual data series, are presented in Figure 1 for key variables of the model. It is evident that the non-linear simulation does not track the actual data as accurately as the linear simulation, particularly in the last few quarters of the sample period. One interpretation of this is that the relevant relationships suffered a major “structural change” at that time.[28]
Counterfactual simulations: an illustration
The responses of the model to an increase in government spending for both linear and non-linear simulation are reported in Figure 2, in terms of deviations from control simulation paths. The two starting periods 1966(3) and 1969(3) are assumed to correspond to a relative trough and peak respectively in economic activity. In general, the non-linear simulations exhibit either a wider cyclical pattern or a more explosive path than the linear simulation.[29] Furthermore, in the non-linear simulation money and prices increase by a considerably larger amount in response to the increase in government spending than is the case with the linear simulation. The linear counterfactual simulation does not in general provide an accurate prediction of the non-linear simulation results for prices and other monetary variables, although this may be related to the unsatisfactory behaviour of the model towards the end of the nonlinear control simulation.
Actual and Control Solution Values
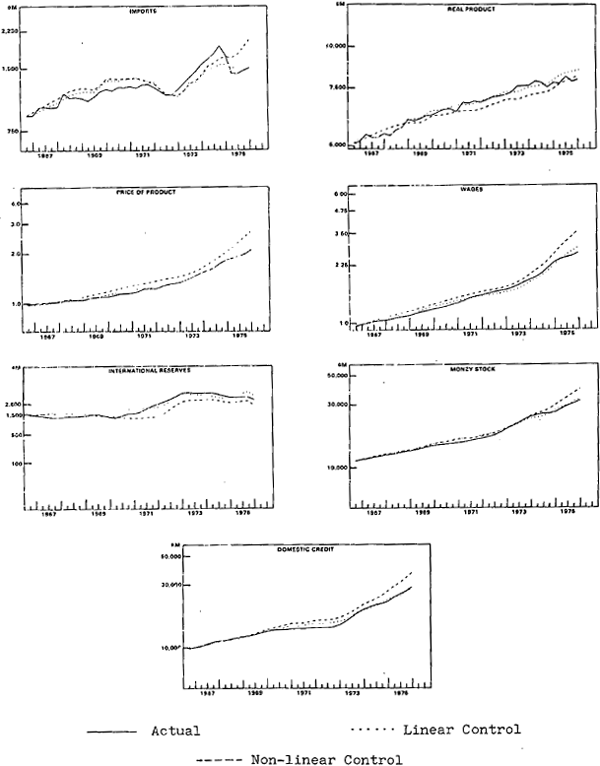
One feature of non-linear simulations is that different patterns of response are obtained when the simulation commences in different time periods. Thus, for example, money and prices show larger deviations from control after 25 periods when the simulation starts from a period of low capacity than from a period of peak capacity. When government spending is increased from a period of high capacity, the initial increase in imports is larger than the response when the impulse is applied in a period of low capacity. The output responses from the two starting periods are similar and close to that of the linear model, until 17 quarters have elapsed: this may indicate that some important non-linear capacity effects in the import/output choice have not adequately been specified in the model.[30]
Stochastic Simulation
The non-linear version of the model was simulated with the addition of a random error term to the stochastic equations: the results from 48 repetitions over the period 1966(3)–1975(4) are reported in Attachment D for key variables of the model.[31] For the stochastic simulations, the tables show the mean simulation path and the standard deviation: the actual data values and deterministic simulation path are also shown. The upper and lower limits of a 95% confidence interval for the simulation path can be obtained by adding and subtracting twice the standard deviation from the mean stochastic simulation values. Thus these simulations provide information on the relationship of the deterministic simulation path and of the actual data series to the confidence interval around the mean stochastic simulation path.
Comparison of the actual data series to the stochastic simulation confidence interval provides a measure of the accuracy of the model's tracking performance: preferably the confidence interval will be narrow and contain the actual data series. From the table it can be seen that the actual data series fall within the 95% confidence interval around the mean stochastic simulation path for the whole sample period for prices, wages and reserves; and for all but the last two periods for output and the last period for imports, when the actual data values are below the lower limit of the confidence interval. The actual values for domestic credit and money are below the confidence interval for the last 8 periods of the sample: however, it should be noted that from a measure of the standard deviation relative to the mean stochastic path, the confidence intervals for money, domestic credit, imports and output are narrow when compared with the confidence intervals for wages, reserves and prices.
The relationship between the deterministic and mean stochastic simulation paths provides a measure of the asymptotic bias of the deterministic solution. For this version of the model, the mean stochastic path is quite close to the deterministic path up to the beginning of 1974 for all variables; and for money, domestic credit and output the deterministic simulation is within the 95% confidence interval for the whole sample period. For prices, wages and imports the deterministic simulation values are higher than the upper limit of the confidence interval for the last few periods, while for reserves the deterministic simulation value is below the lower limit of the confidence interval for 1975(4). Thus bias in the deterministic simulation does not become evident until the last few quarters of the sample period.
Post-Sample Performance
When the non-linear model is simulated beyond the sample period, the simulation fails in period 1976(2) when the predicted value of international reserves falls to zero. This is associated with a rise in imports and wages from 1974(4), and suggests the need for re-estimation of the model over a longer time period, and perhaps some respecification.[32] An investigation into the use of “linearisation variables” as introduced by Bacon and Walters (1978) has indicated their usefulness in providing a better prediction of international reserves. These variables, which ensure that the linearised identities hold for the actual data, are added to the linearised identities at the estimation stage and although for this version of the model four of the parameter estimates changed sign,[33] the non-linear control simulation is obtainable to the end of the period whereas the model without the linearisation variables fails when reserves fall to zero. These variables are used in the estimation of recent versions of the model.
Suggestions for further work
One of the problems with this approach to non-linear simulation is that it is based on parameter estimates for a linearised version of the model. However, the most frequently used alternative approach to full system estimation and simulation is to estimate the model by, possibly non-linear, single equation techniques and to simulate the non-linear model as a full system. This approach, which does not use information from the covariance matrix of equation residuals at the estimation stage, may not be any better than the approach which involves linearisation for estimation. A comparison between the full non-linear simulation of the model estimated by FIML and by OLS is reported in the next section.
Another issue illustrated by the non-linear simulations is the importance of the steady-state values used in the linearisation process. These can be used in coding the model for non-linear simulation but, as mentioned above, the derived equation constants were in some cases adjusted to put the model on track in the first simulation period. This may indicate some inconsistency between the steady state values used for estimation, and implied by non-linear simulation. One way to obtain estimates of the steady state values of the model is to iterate between estimation of the linearised model, and non-linear simulation for one period.[34]
Even though it is not feasible at present to obtain pseudo full-information maximum-likelihood estimates of a non-linear system of the size of RBA76, there may be scope for obtaining non-linear full information estimates of blocks of the RBA76 model. However, the choice of appropriate blocks of the model is not an obvious one.
Footnotes
Bacon and Johnston (1977) include a discussion of the linearisation process. [24]
If the sample contains a period when the economy may be a long way from the steady state path, the “star” values calculated from the estimated constants of the regressions may be biased estimates of the steady state values. [25]
As used by Trevor (1978). [26]
Two simulation programs were used: the non-linear simulation program (Apredic) in the Wymer package, and Simulator from the Bank of Canada package. The solutions from each program differ slightly, due to the different degrees of accuracy involved in the iterative procedures to obtain values of the endogenous variables for each time period. The Simulator program was used for simulation of the OLS model reported in the next section. [27]
Estimation of RBA76 over different sample periods, reported in Taylor (1979), indicates that the 1974 data are a major cause of the “parameter instability” noted by Porter (1977). [28]
This reinforces the point made by Blatt (1978). [29]
Recent versions of the model have been respecified in the light of these results. [30]
The shocks are a randomly weighted average of the single equation residuals over 20 periods with the same variance-covariance and distributional properties as the estimated error terms of the non-linear model, and are redefined for each period to be simulated. The stochastic simulations are carried out on an adjusted version of the model (see fnl on p21) since reserves fall to zero before 1975(4) when shocks are applied to the unadjusted model. [31]
The prediction of reserves can be prevented from going negative by an adjustment in the form of adding a synthetic variable which operates from 1974(4) to the equations for imports, wages and labour demand. However, as alteration to the model at the simulation stage is a procedure of unknown statistical properties, the adjustment could only be considered an expedient measure until more analysis and respecification can be done. [32]
These were the parameters on the world interest rate and relative price term in desired money, and inventory disequilibrium and monetary disequilibrium in the labour demand equation. [33]
Wymer (1979). [34]