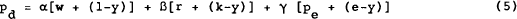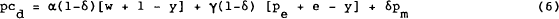RDP 8713: Estimating the Inflationary Effects of Depreciation Appendix 1: The Mark-up Model of Inflation

Let the aggregate price of consumer goods be PC_d. This is a weighted combination of the price of domestically-produced consumer goods, P_d, and the price (in domestic currency) of foreign-produced consumer goods P_f:

where δ is the weight, and can be thought of as the import penetration ratio.

P_d can be thought of as a mark-up on costs of production. Let the production function for domestic consumer goods be represented by

where K and L represent capital and labour, respectively, and E represents energy input, along the lines proposed by Helliwell et al.^[1] If F is homogeneous of degree one, then competitive equilibrium requires that

where W is the wage rate, R the rental cost per unit of capital and P_E the price per unit of energy. This then implies that

– the unit price is the sum of the unit costs for labour, capital and energy.

If lower case letters are used for proportionate rates of change, then for small changes, the rate of change of P_d is approximately given by

where α, β and γ are the proportions of labor, capital and inputs into the productive process (α + β + γ = 1). If unit capital costs do not change, the second term is zero, and price movements are left as being explained by changes in unit costs of labour and energy.

If an import price index, P_m, is used to represent P_f, and rates of change of (1) are taken and (5) substituted into the resulting equation, the following equation is obtained:

Allowance can be made for the fact that the economy could be off this competitive pricing relationship in the short run. A conventional approach is to allow some lagged adjustment, as in (7):

Because labour productivity as measured may contain a large component of noise, trend productivity growth may be used. This can be accomplished either by allowing a separate constant term in (6), or (which amounts to the same thing) by specifying the unit labour cost variable as w_t−i−z, where z is the trend growth rate of productivity. In addition to this, the “energy productivity” term in (7) can be subsumed into a constant.

It is difficult to think of any satisfactory direct measurement of unit capital costs.^[2] However, because rates of return to capital may vary with the economic cycle, a demand-pressure term can be included to proxy movements in profit margins and hence in returns to capital. A typical variable is the deviation of output from some trend growth path, denoted below as D.

The specification that is obtained is then

where b_i = α(1−δ)η_i, and c_i = γ(1−δ)θ_i and ϕ_i = δμ_i.

It can be seen that (8) embodies the restrictions that:

• the mix of inputs in the productive process (described by α, β and γ) does not change;
• the change in the efficiency of use of energy (the (e-y) term in (7)) is zero, or some non-zero constant;
• changes in unit capital costs (r + k − y) are only cyclical (and are captured by D), or trend (and are thus picked up by a);
• the import penetration ratio (δ) is constant, when in fact it may, and almost certainly will, vary over time.

Given that these restrictions are imposed, one might expect to find the performance of the model deteriorating under some plausible conditions:

• if over time the relative proportions of labor, capital and energy in the productive process altered, consumer prices might become more or less sensitive to changes in wages;
• if capital costs increased sharply, the model would underpredict the rise in prices;
• the model will under or over-predict the effect of import prices as the import penetration ratio rises above or falls below its sample mean.

An additional feature of the pure mark-up model discussed above is that it ignores the important notion of substitutability between domestic and foreign goods. In the context of (1), allowance for substitutability might be expressed as:

In the event of a substantial currency depreciation by a small country, the price of imports will rise (abstracting from “absorption”). Prices of domestic substitutes may be expected to rise as well – the greater the cross elasticities, the greater the rise in domestic prices. In the extreme case of perfect substitutes and atomistic world markets, P_d will move up to the new world price measured in domestic currency (i.e. ∂P_d/∂P_f = 1), and the rise in domestic prices will be exactly equal to the rise in import prices (i.e. ∂PC_d/∂P_f = 1).

In the more general case of significant but imperfect substitutability the sum of the estimates of the d_i in equation (8) is likely to be of a larger magnitude than the import penetration ratio (or in a computational sense, the weight of imported goods in the price index used), since it will pick up a substitution effect.

Footnotes

See Helliwell, Boothe and McRae (1982). The specific effect to be captured here is the importance of oil in the productive process, and thus of oil prices for prices generally. [1]

Excluding the effect of changes in the capital-output ratio (K/Y), unit capital costs are explained by movements in R, the aggregate rate of return to capital. Measurement of this rate of return is, however, close to impossible. Its short-term movements are probably not well-proxied for the present paper by any conventional market interest rate. In the longer term, excluding the possibility of secular shifts in real rates of return or in inflation rates, it may be safe to assume that the rate of return to capital does not substantially change, and that nor in turn do unit capital costs. [2]