RDP 8713: Estimating the Inflationary Effects of Depreciation 5. The Effects of the Depreciation

This section describes a “no-depreciation” counterfactual simulation, using the CPI model described in Section 3 and estimated in Section 4.

(a) Import Prices

The major effect of the depreciation upon domestic prices will be from its effect upon import prices. The equation estimated in Section 4(b) can be used to obtain an estimate for the effect of the depreciation upon import prices.

The equation estimates an increase in import prices over the two years to December 1986 of 44.4 per cent, compared with an actual increase of 42.7 per cent. Using the parameters of that equation, and the assumption that the exchange rate remains unchanged from its December quarter 1984 level of TWI=81.8, the “no-depreciation” path for import prices (in twelve-months-ended change form) is shown, along with the in-sample estimates and actuals, in Figure 3 below.

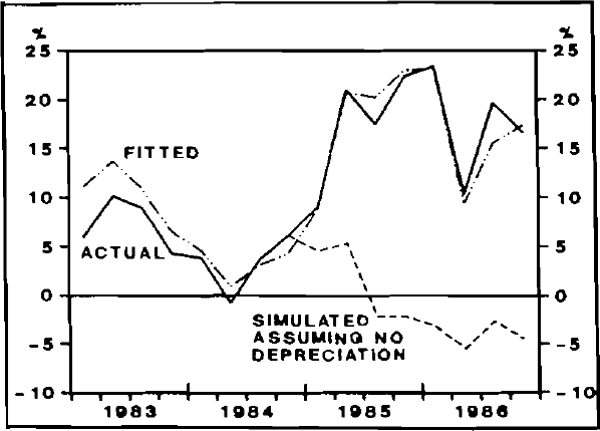
The counterfactual simulation suggests that the depreciation boosted import prices by nearly 50 per cent in the two years to to end-1986. This suggests that import prices might have fallen by around 5–1/2 per cent over the same two year period if the the exchange rate had not depreciated.

This finding can be compared with the experience of other industrialised countries. To this end data (shown in Appendix 2) for import prices for 16 other OECD countries were collected. All sixteen countries show falls in import prices (measured in their own currencies) over the twelve months to September 1986, except for Norway, where there was no change in import prices over the period. This was despite the fact that a number of the countries experienced substantial depreciations over the period. Some further figuring, also in Appendix 2, suggests that after removing the effects of changes in exchange rates and oil prices, import prices fell, on average, by around 7 per cent in the year to September 1986 in these countries. Thus the finding above that, had it not been for the depreciation, Australia might have been experienced falling import prices is consistent with the experience of other countries.

(b) Domestic Prices

To estimate the total effects of the depreciation upon the domestic price level, the mark-up model estimated in the previous section is used for a counterfactual simulation. For this purpose:

• the “no depreciation” path for import prices generated in Section 5(a) is used;
• the effect of the depreciation is removed from petrol prices, based on calculations by the Prices Surveillance Authority; and
• wages under the “no-depreciation” scenario are assumed to be unchanged from the actual historical outcome.

For petrol prices, the Prices Surveillance Authority has dissected changes in the maximum wholesale price of petrol into the effects of exchange rate changes, supply cost changes and changes in excise and other government charges.^[16] The removal of the exchange rate effect from petrol prices reduces petrol prices in the December quarter 1986 by around 12–1/2 per cent.

The path generated for the CPI excluding health under these assumptions is plotted against the estimated path generated by the sample data, as well as the actual outcome, in twelve-months-ended form in Figure 4 below.^[17]

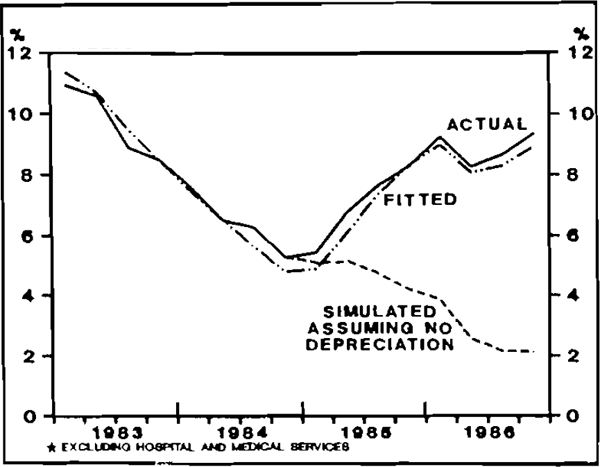
Using historical data for the eight quarters to December quarter 1986, the model estimates that the CPI (excluding health) grew by 18–1/2 per cent. Over the same period, the “no-depreciation” simulation shows growth of only 6–1/2 per cent, suggesting that the depreciation contributed around 12 percentage points to the CPI over the two years. The model implies a total long run effect of the depreciation of the order of 18 percentage points.^[18] Given the depreciation of around 51 per cent against the TWI (when measured in units of domestic currency per unit of foreign currency), this would imply that the CPI responds to changes in the TWI with an elasticity of around 0.35.

The estimates for the effect of the depreciation upon the CPI are shown in quarterly form in Figure 5 below, along with the Statistician's estimates of the direct contribution of increases in the prices of goods and services which are wholly or predominantly imported.

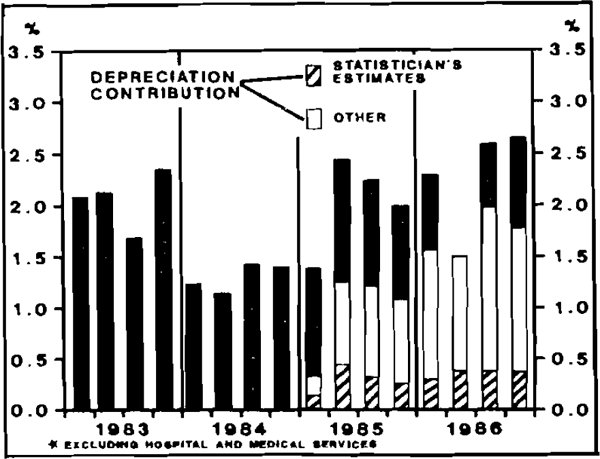
Not too much importance should be placed on the particular point estimate of the depreciation effect. There is likely to be some simultaneity bias. For example, had there been no depreciation, wages may have behaved differently.

While there was explicit discounting for at least part of the depreciation effect at National Wage hearings, earnings “drift” was quite strong over 1986. Wage growth could easily have been lower had the depreciation not occurred. This suggests that the estimates of the depreciation effects could be too small. On the other hand, economic policies generally, particularly monetary policy, were tightened as a result of the same circumstances which produced the depreciation, implying slower inflation than would otherwise have occurred. This imparts some bias in the other direction. It is not possible to be certain how these effects will net out in the final analysis.

But it remains to be said that the findings here are of interest since they suggest that the responsiveness of domestic prices to the exchange rate is greater than has been found in most earlier studies. Fallon and Thompson (1987), for example, cite three earlier studies^[19] which show, according to their calculations, total exchange rate “elasticities” of around 0.23, compared with this study's estimate of 0.35. Fallon and Thompson themselves use a completely different methodology, applying the IAC's ORANI model to capture the effects of depreciation upon the different sectors of the economy. Their analysis is more detailed, and includes an explicit consideration of capital rental costs. Their results show a total elasticity of around 0.36, supporting the notion of a larger effect. Furthermore, they are able to calculate effects on various types of goods, for example exportable, import-competing, and non-tradeable goods. The estimates of this paper might be regarded as complementing the Fallon and Thompson estimates, by providing an estimate of the timing of these depreciation effects.^[20]

Footnotes

Because the Import Parity Price is calculated against the U.S. dollar, these calculations show the effect upon petrol prices of our depreciation against the U.S. dollar, rather than against the TWI. [16]

Note that Figure 4 shows a counterfactual path for the CPI excluding hospital and medical services, which in the year to December 1986 grew substantially faster than the rest of the CPI. If it is assumed that the prices of hospital and medical services have been affected by depreciation to a similar extent to the rest of the CPI the counterfactual simulation for the total CPI would be higher by around 0.5 percentage points in the year to December 1986. [17]

Some rough calculations for the March, June, and September quarters of 1987 suggest a further depreciation effect of around another four percentage points, suggesting that only a relatively small proportion of the total effect was then yet to impact upon the CPI. [18]

By the Treasury (NIF-10), Nevile and the Economic Summit Model. [19]

It should be noted that the estimates of this paper use calculations of the effect of changes in the $A/US$ rate upon petrol prices, based on existing government revenue arrangements. Fallon and Thompson appear, however, to assume that petrol prices would be affected by the full magnitude of depreciation, which in the current example is around 51 per cent on a trade-weighted basis. If the calculations of this paper were made under similar assumptions, the total elasticity obtained would be somewhat higher. [20]