RDP 8713: Estimating the Inflationary Effects of Depreciation 4. Estimation Results

Tony Richards and Glenn Stevens

December 1987

(a) Domestic Prices

The dependent variable is the CPI excluding health. Dummy variables have been included to capture seasonality. Other factors, such as the effects of droughts or floods on food prices, and irregular increases in government charges, continue to affect the data.[9]

The energy price variable is an index of automotive fuel prices obtained from the ABS. As a result the estimates obtained for the energy prices variable are a measure of the sum of the direct and indirect effects of fuel prices on the CPI.

A demand pressure variable is included to capture any short-term variations in the return to capital. The variable used is the deviation of non-farm GDP from its trend over the period.

The first estimation issue to be addressed is the length of the lags on the effects of the explanatory variables upon the CPI. Previous Australian studies indicate lags of up to 6 quarters from both wages and import prices; the initial specification follows suit.

Results for the initial equation, estimated using ordinary least squares from 1972(4) to 1986(4), are shown in column 1 of Table 1. The point estimate of the sum of effects from all lags of the three explanatory variables is less than unity. The estimated coefficients on some lags are negative; many estimates have large standard errors.

Table 1: Estimation of the CPI Equation*
  1 2 3 4 5
Estimation Period 72(4)–86(4) 76(4)–86(4) 78(2)–86(4) 78(2)–86(4) 78(2)–86(4)
Lag Specification Freely Estimated Freely Estimated Almon Almon Freely Estimated
Intercept 1.01
(3.8)		 .83
(2.4)		 .52
(1.6)		 .07
(0.9)		 .18
(1.8)
W(0) .09
(2.1)		 − .01
(0.2)		 − .01
(0.3)		 .04
(1.1)		 .10
(2.1)
W(−1) .09
(1.9)		 .12
(2.2)		 .11
(2.1)		 .14
(4.0)		 .19
(4.2)
W(−2) −.06
(0.1)		 −.02
(0.2)		 .08
(2.5)		 .10
(2.9)		 −.01
(4.0)
W(−3) .03
(0.5)		 .04
(0.7)		 .04
(1.2)		 .05
(1.8)		 .07
(1.3)
W(−4) .12
(2.3)		 .16
(2.6)		 .05
(1.9)		 .07
(3.0)		 .16
(3.4)
W(−5) .15
(2.7)		 .05
(1.0)		 .10
(2.2)		 .11
(3.3)		 .06
(1.4)
W(−6) .05
(0.9)		 .07
(1.1)		 .11
(2.0)		 .08
(2.2)		 .05
(1.2)
PM(0) .05
(1.7)		 .56
(1.8)		 .04
(1.4)		 .05
(2.8)		 .06
(3.0)
PM(−1) .01
(0.5)		 .01
(0.3)		 .04
(2.5)		 .06
(6.8)		 .02
(0.8)
PM(−2) .04
(1.2)		 .0
(.0)		 .03
(2.3)		 .06
(5.8)		 .09
(3.5)
PM(−3) .02
(0.6)		 .03
(1.2)		 .03
(1.9)		 .05
(4.5)		 .05
(2.1)
PM(−4) .05
(1.6)		 .02
(0.6)		 .03
(1.9)		 .05
(4.5)		 .06
(2.4)
PM(−5) .0
(0.1)		 .02
(0.6)		 .02
(1.9)		 .04
(4.3)		 .01
(0.6)
PM(−6) −.01
(0.4)		 .01
(0.2)		 .02
(0.8)		 .02
(1.4)		 .04
(1.8)
Petrol(0) .06
(3.5)		 .06
(4.9)		 0.05
(5.1)		 .045
–		 .045
–
Petrol(−1) 0
(0)		 0
(0.3)		 0
(0)		 .01
(1.1)		 0
(0)
Petrol(−2) .01
(0.4)		 0
(0.2)		 0
(0.3)		 0
(0.9)		 .01
(1.3)
Petrol(−3) .02
(1.2)		 .02
(1.3)		 0
(0.4)		 0
(0.4)		 .01
(1.1)
Petrol(−4) −.03
(1.7)		 −.01
(0.6)		 0
(0.6)		 0
(0.5)		 .02
(1.6)
Petrol(−5) .01
(0.5)		 .02
(1.5)		 .01
(0.7)		 .01
(1.0)		 0
(0)
Petrol(−6) 0
(0.1)		 .01
(0.8)		 .01
(0.5)		 .01
(1.3)		 .01
(1.0)
Demand 15.6
(2.9)		 9.9
(1.9)		 6.0
(1.2)		 –
 		 –
 
Dec 78 Excise –
 		 –
 		 –
 		 1.20
–		 1.20
–
ΣW .48 .41 .48 .59 .61
ΣPm .02 .12 .21 .32 .33
Direct Petrol .06 .06 .05 .045 .045
Σlndirect Petrol .06 .04 .02 .04 .01
Σ all .61 .64 .77 1.00 1.00
DW 2.03 1.31 2.40 2.15 1.74
Inline Equation .70 .63 .67 .78 .82
Restrictions – – Pet (0) = .045 Pet (0) = .045
      Σ all = 1.00 Σ all = 1.00
      Excise = 1.2 Excise = 1.2
F statistics on Restrictions
(incl. Almon restrictions) 		  0.85
 		 1.23
 		 0.63
 
Critical 5% F     2.59 2.91 3.71
n 57 41 35 35 35
df 31 15 29 22 13

* t statistics in parentheses. Seasonal factors omitted for convenience.

There could be a number of reasons for these problems. The large number of lags in the specification necessitates a long run of data, over a period when structural change was almost certainly occurring. Those changes had several distinct manifestations. Importantly for the link from import prices to the domestic price level, the import penetration ratio rose steadily through the 1970s and early 1980s.[10] In addition, changes in capital intensity in the wake of the mid 1970's wages explosion could have altered the responsiveness of prices to wage and capital costs.

To explore the question of structural change, an equation excluding the first four years of data from the sample is shown in column 2 of Table 1. Applying a Chow test, the null hypothesis of no structural change can be rejected at the 5 per cent level of significance.

Instability in the behavioural parameters could account for this. But other factors may also be important. It could be that the variance of the disturbance terms is different in the two periods. This could be so if, for example, inflation in the mid 1970s was more variable than in subsequent years.

In view of the above, a shorter estimation period was used, from 1978(2) to 1986(4), during which the problem of structural change should be less pronounced. To overcome a shortage of degrees of freedom, the Almon technique was employed to restrict the lag structure to be polynomially-distributed. The results are shown in column 3 of Table 1.[11]

In a further refinement in the preferred equation, shown below in Table 2 and in column 4 of Table 1, the coefficients on the three input price variables are restricted to sum to unity, and the direct (i.e. lag zero) petrol price effect to be 0.045, which is approximately equal to its average weight in the CPI over the estimation period. The demand pressure variable is omitted, because of the insignificant parameter estimates obtained in earlier equations (though insignificant petrol price variables are retained). A synthetic variable is included to capture the effects of a significant increase in excise rates on alcohol and tobacco prices in the December quarter of 1978.

Table 2: Preferred CPI Equation (Almon Lags)
(t statistics shown in parentheses)
  wt−i Pmt−i Petrolt−i Intercept
LAG 0
 		 .041
(0.6)		 .051
(2.1)		 .045
–		 .07
(0.9)
  1
 		 .145
(1.8)		 .055
(3.9)		 .009
(1.1)		 Dec 78 Excise
  2
 		 .088
(2.9)		 .056
(3.9)		 .005
(0.9)		 1.20
 
  3
 		 .053
(4.9)		 .053
(3.3)		 .003
(0.4)		 Seasonals
 
  4
 		 .066
(5.1)		 .047
(3.2)		 .003
(0.9)		 March −.12
(0.9)
  5
 		 .122
(3.4)		 .036
(2.3)		 .007
(0.9)		 Dec. .20
(1.7)
  6
 		 .079
(2.5)		 .023
(0.6)		 .012
(0.8)		  
    Σ=.595
 		 Σ=.322
 		 ΣDirect = .045
Σlndirect = .039		  
Estimation period: 1978(2) – 1986(4), n=35, df=22
DW = 2.15 R2 = 0.85 Inline Equation= 0.78
 
Restrictions: Σ all = 1.00,  
  Petrol (0) = .045,  
  Dec ′78 Excise = 1.20.  
F statistic on restrictions = 1.23, Critical 5% F= 2.91

The three restrictions could not be rejected jointly at the 5 per cent level. The Durbin-Watson statistic, though close to 2, was in the inconclusive region at the five per cent level of significance, due to the relatively large number of regressors. A Box-Pierce test could not reject the hypothesis that the residuals were free from first to twelfth-order autocorrelation (though it should be noted that, in this instance, this is not a powerful test).[12]

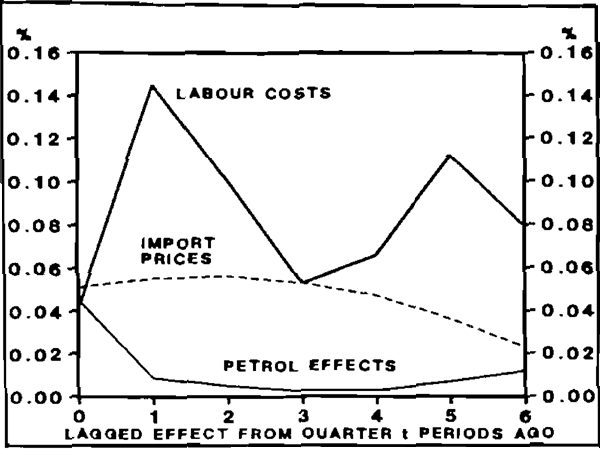
The estimated coefficients in the preferred equation shown in Table 2 indicate total weights for unit labour costs and import prices of .59 and .32 respectively, and 0.05 and 0.04 respectively for the direct and indirect petrol effects. The pattern of each effect is shown in Figure 2 below.[13]

Figure 2: LAG STRUCTURES AND INFLATION
ESTIMATES 1978(II) – 1986(IV)
Figure 2: LAG STRUCTURES AND INFLATION

(b) Import Prices

For import prices, Equation 2 was estimated using ordinary least squares. For this purpose, the world price index was converted into domestic currency terms, using the Trade Weighted Index of the Australian dollar. The weights in that index are based on import as well as export shares, but they are not much different to the weights in the world price index. The world price and exchange rate variables were collapsed into a single variable representing foreign export prices in Australian currency units. (An F-test showed that the hypothesis of similar lag coefficients on each could not be rejected.)

The equation is estimated from the early 1970s, when the TWI was first calculated. It shows fairly short lags, with the full effect from foreign prices and exchange rates being reflected in import prices within about four quarters.

In preliminary estimations the equation substantially underpredicted the 9.3 per cent increase in import prices that occurred in the September quarter of 1973. It seems plausible that the residual (nearly twice as large as any other residual in the estimation) is related to the 25 per cent across-the-board tariff cut of 18 July 1973. Since the dependent variable measures import prices before tariffs and quotas, the large rise in import prices in that quarter could reflect foreign suppliers lifting their home-currency prices to absorb some of the benefits of the tariff cut. Accordingly, in refining the equation, a synthetic variable for the tariff cut is included, taking a value of 3.0 per cent in 1973(3).[14]

A further refinement is to test and then impose the restriction that the sum of the lag coefficients on the foreign price variable is unity, in order to assess the hypothesis of full pass-through from changes in world prices and in the exchange rate.

The equation resulting from these modifications is shown in Table 3 below.

Table 3: Preferred Import Price Equation
(t statistics shown in parentheses)
pm = −.04 + .49 e pw + .34 e.pw (−1) − .03 e.pw (−2) + .19 e.pw (−3)
(0.2) (11.1) (7.7) (0.6) (3.9)
+ Tariff Variable  
Estimation period: 1972(3)–1986(4), n = 58, df = 54
DW = 2.30 R2 = .76 Inline Equation = .75  
Restrictions: Σe.pw =1,      
  Tariff = 3.0.      
F statistic on restrictions = 1.89, Critical 5% F = 3.18

The estimates obtained are in line with expectations, except for a negative estimate on the second lag of the foreign price variable. The coefficient was, however, statistically insignificant. The restrictions on the sum of elasticities and the tariff variable could not be rejected at the 5 per cent level of significance.[15] The Durbin-Watson statistic indicates the absence of first-order auto-correlation, while a Box-Pierce test did not reveal any higher-order auto-correlation.

Footnotes

There is still a considerable amount of “noise” in the data. Using annual or semi-annual data would eliminate much of this variation. But if non-overlapping data are used, this has the effect of substantially reducing the effective number of observations, while the alternative of using a larger sample of overlapping periods introduces the problem of auto-correlated errors. [9]

The ratio of exports to GDP also rose over this period. This would be a further reason for instability because of the influence of domestically-consumed exportables in the CPI. An export price variable was not included, however, because of the already large number of explanatory variables. [10]

There are, of course, a number of problems in the use of Almon lags. However, the results which were obtained do not appear to be peculiar to the choice of the Almon lag formulation. The polynomial lags for each variable were fitted using the method suggested in the literature on distributed lags. (See, for example, Trivedi and Pagan (1976).) Longer lag structures were tested but the hypothesis that the lag length was only six quarters could not be rejected. Tests for the appropriate degrees for the polynomials indicated that a second-order polynomial could describe the lags on import prices and petroleum prices, but that a fourth order polynomial was required to describe the lag structure on unit labour costs. The restrictions implied in the Almon lag formulation, were tested against a freely estimated equation and could not be rejected. Furthermore, the estimates obtained for the weights on each variable in the Almon lag equations are very similar to the freely-estimated weights. This suggests that the results derived below for the long run effect of import price (and exchange rate) changes would be valid without assuming Almon lags. [11]

An examination of the correlation matrix of the regressors indicated both the import price variable and the petroleum price variable tended to be reasonably highly correlated with their own lagged values. However, as Belsley (1986) points out, it is the collinearity or conditioning of the original data series and not the first-differenced series which is important for the reliability of the estimates. An examination of the collinearities of the original series (using the method suggested by Belsley, Kuh and Welsch (1980)) suggests that the important collinearities in the data are limited to the different lags of the same series. This will lead to inefficient estimates of the particular lag structures but should have less effect upon the estimates for the total effect from each series. This suggests that collinearity amongst the dependent variables is unlikely to have had a major effect upon the estimates which are of the most interest in the present study. [12]

The weights on the preferred equation which employs Almon lags can be compared with the weights from a freely estimated lag structure where the weights are also constrained to sum to unity. As can be seen in column 5 of Table 1, the estimated weights for each variable are quite similar suggesting that the coefficient estimates are not peculiar to the assumption of Almon lags. Furthermore, in neither case could the restriction that the weights summed to unity be rejected. [13]

When a dummy variable for the tariff cut is freely-estimated in the equation it shows a once-off effect of over 6 per cent. Some simple calculations suggest this is too high. If the average tariff rate for endogenous goods were 15 per cent, the tariff cut would have cut average tariff rates to 11.25 per cent. This would imply that foreigners could lift their home-currency prices by up to 3.4 per cent without increasing their Australian dollar after-tariff price. [14]

The finding of full pass-through (with quite short lags) from changes in world prices and exchange rates is consistent with the findings of the Bureau of Industry Economics (BIE, 1986). Those survey results imply that changes in the exchange rate in 1985 were reflected almost fully in prices paid by importers with relatively short lags.

A further finding of that survey was that importers were slow to pass through the full effects of their cost increases to retailers or final users. There is, however, no reason to expect that this will adversely affect the estimates of the following two sections of the effect of exchange rate changes upon the CPI. In particular, the conditions which might cause changes in importers' margins have existed at other times in the sample period, so it is likely that this type of “absorption” has also occurred at other times in the sample. As a result, the effect of any slow pass-through from import prices to final prices is likely already to be captured in the estimated CPI equation. [15]