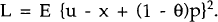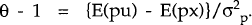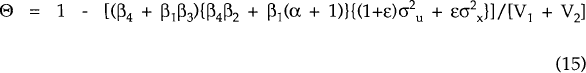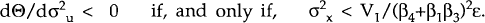RDP 8909: Optimal Wage Indexation, Monetary Policy and the Exchange Rate Regime 3. The Optimal Degree of Wage Indexation
December 1989
- Download the Paper 753KB
The optimal degree of wage indexation is defined as that which makes the ex-post real wage as close as possible to the market clearing real wage. Specifically, the social objective is to minimize the following loss function:[11]
where E is the expectations operator and (w – p)* is the real wage that clears the labour market.
Following the usual practice in the literature, I assume labour supply to be completely wage inelastic and non-stochastic. It is then trivial to show that the real wage innovation that clears the labour market is equal to u, the productivity shock. Substituting for p and w, the loss function becomes
Minimizing L with respect to θ yields
Using (13) and the assumed orthogonality of the shocks, the optimal degree of wage indexation is obtained:
| where | V1 | = | (β4β2)2(σ2ξ + σ2υ) + β24(σ2κ + σ2s) + β21(σ2δ + σ2τ), |
| V2 | = | (β4 + β1β3)2σ2u(1+ε). |
The optimal degree of wage indexation, Θ, is thus a function of the structural parameters and the variances of the shocks. Θ varies positively with the degree of flexibility in the nominal exchange rate. Given the variances of the shocks, the loss function (14) can be minimized with a high degree of wage indexation and a relatively flexible exchange rate, a low degree of wage indexation and a relatively fixed exchange rate, or some combination of the above.
Inspection of (15) also reveals that it is consistent with the Gray-Fischer result that the optimal degree of wage indexation increases as the variance of the demand side shocks increases, and that, in the absence of real shocks, Θ is equal to unity. However, it is not clear that another standard result of that literature holds – that Θ decreases as σ2u increases. In fact, differentiation of (15) with respect to σ2u reveals that
In the presence of wage shocks, the optimal degree of wage indexation is not necessarily decreased when the variance of productivity shocks increases. Whether this is the case is an empirical question. (In the Gray-Fischer formulation σ2x and so no ambiguity arises).
Footnote
A standard objection to this definition of optimality is that efficient wage contracts will not be restricted to the information contained in the price level; they will be contingent on a range of variables. Nevertheless, for reasons of analytical tractability, I only consider the type of indexing scheme above. [11]