RDP 8909: Optimal Wage Indexation, Monetary Policy and the Exchange Rate Regime 5. Results
December 1989
- Download the Paper 753KB
The estimation results are reported in Tables 2 and 3. The estimates of the wage indexation parameter, θ, are shown in the first column of Table 2. They range from a low of 0.041 for Canada to a high of 0.662 for Austria. One should emphasize that these results do not imply, for example, that nominal wages were almost rigid in Canada over the sample period. Rather, they imply that, over this period, unanticipated Canadian inflation had practically no effect on Canadian nominal wages. In Austria, on the other hand, about two-thirds of unanticipated inflation was passed through to wages growth. The divergences in the estimated values of θ reflect differences in (perhaps implicit) wage contracts in these nine countries. The estimates of θ are reasonably well-determined, being significantly different from zero (at the ten percent level) in the majority of cases.
| COUNTRY | ESTIMATED PARAMETERS | |||||
|---|---|---|---|---|---|---|
| θ | α | γ | π1 | π2 | π5 | |
| Australia | 0.125 (0.703) |
0.300 (0.885) |
1.000 * |
0.064 (0.051) |
0.004 (0.026) |
0.199 (0.056) |
| Austria | 0.662 (3.083) |
1.357 (3.363) |
1.000 * |
0.100 * |
0.085 (0.027) |
0.135 (0.070) |
| Canada | 0.041 (0.067) |
0.137 (0.847) |
1.000 * |
0.101 (0.032) |
0.022 (0.053) |
0.158 (0.060) |
| France | 0.144 (0.085) |
2.250 (1.931) |
1.000 * |
0.052 (0.019) |
0.013 (0.025) |
0.131 (0.077) |
| Germany | 0.117 (0.060) |
2.360 (3.197) |
1.000 * |
0.316 (0.105) |
0.017 (0.047) |
0.205 (0.085) |
| Italy | 0.391 (0.210) |
0.595 (0.640) |
1.000 * |
0.328 (0.060) |
0.070 (0.044) |
0.100 * |
| Japan | 0.253 (0.085) |
4.320 (3.697) |
1.000 * |
0.228 (0.077) |
0.001 (0.020) |
0.143 (0.058) |
| UK | 0.607 (0.287) |
1.021 (2.241) |
1.000 * |
0.100 * |
−0.016 (0.018) |
0.357 (0.113) |
| US | 0.108 (0.277) |
1.699 (1.920) |
0.494 (0.966) |
0.534 (0.107) |
0.010 (0.037) |
0.100 * |
Standard errors in parentheses |
||||||
| COUNTRY | VARIANCES OF THE SHOCKS* | ||||||
|---|---|---|---|---|---|---|---|
| Supply | Demand | ||||||
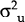 |
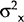 |
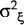 |
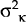 |
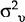 |
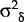 |
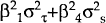 |
|
| Australia | 0.112 | 0.153 | 1.585 | 0.354 | 0.007 | 0.389 | 23.386 |
| Austria | 0.048 | 0.165 | 0.098 | 0.018 | 0.014 | 0.411 | 1.549 |
| Canada | 0.042 | 0.003 | 0.185 | 0.201 | 0.011 | 0.604 | 6.271 |
| France | 0.017 | 0.006 | 0.422 | 0.057 | 0.012 | 1.560 | 10.072 |
| Germany | 0.030 | 0.004 | 0.540 | 0.162 | 0.009 | 0.417 | 0.864 |
| Italy | 0.032 | 0.016 | 0.374 | 0.314 | 0.010 | 0.206 | 0.756 |
| Japan | 0.028 | 0.008 | 1.568 | 0.222 | 0.008 | 0.758 | 1.209 |
| UK | 0.014 | 0.010 | 1.154 | 0.031 | 0.010 | 0.332 | 3.798 |
| USA | 0.019 | 0.016 | 0.548 | 0.123 | 0.020 | 0.115 | 0.349 |
* ×1000 |
|||||||
The second column of Table 2 shows the estimated values of α, the money-reaction parameter. These reveal a wide variety of monetary reactions across countries. However, the standard errors of these estimates are uncomfortably large; the difficulty in obtaining robust estimates for α might be due to changes in the way monetary policy was conducted in these countries over the sample period.
In all cases except for the United States, the parameter γ in the price equation was estimated to have the wrong sign. This created a problem since the concept of optimal wage indexation makes little sense if the aggregate supply curve has a negative slope. At the very least, such an occurrence suggests the possibility of a dynamically unstable model. This difficulty was resolved by imposing a positive value for γ. A value of unity was chosen; this choice did not substantially affect the estimated value of Θ, and so did not affect the test of whether the degree of wage indexation was optimal.
The third, fourth and fifth columns of Table 2 report the estimated values of the parameters of the aggregate demand equation (16), π1, π2 and π5. Turning first to π2, the results show that, for almost all countries, innovations to the real exchange rate have only small effects on innovations to aggregate demand. The estimates of π1 and π5 show that for nearly every country innovations to the growth of money and real government expenditure have important effects on unexpected output growth. These are robust results; in many cases the parameter estimates are significant at the one percent level.
Together with the estimated variances of the shocks (reported in Table 3), the parameter estimates are used to derive the estimates of the optimal degree of wage indexation, Θ. These are shown in the first column of Table 4. They range from a low of about 30 per cent for the Austria and the United States to a high of about 90 per cent for Australia, Canada, France and the United Kingdom. In the Australian case, for instance, the reason that Θ takes on such a high value is due to two factors, the relative dominance of demand shocks and the relative flexibility of the exchange rate, as reflected in a low value of α (i.e. innovations to money growth in Australia have been relatively insensitive to innovations in the inflation rate).
| COUNTRY | ESTIMATED PARAMETERS | ||||
|---|---|---|---|---|---|
| Θ | σ2Θ | θ | σ2θ | Wald | |
| Australia | 0.902 | 0.023 | 0.125 | 0.494 | 1.165 |
| Austria | 0.285 | 0.579 | 0.662 | 9.507 | 0.014 |
| Canada | 0.926 | 0.005 | 0.041 | 0.005 | 85.947* |
| France | 0.890 | 0.008 | 0.144 | 0.007 | 35.713* |
| Germany | 0.649 | 0.138 | 0.117 | 0.004 | 2.000 |
| Italy | 0.728 | 0.016 | 0.391 | 0.044 | 1.889 |
| Japan | 0.518 | 0.167 | 0.253 | 0.007 | 0.405 |
| UK | 0.904 | 0.014 | 0.607 | 0.083 | 0.919 |
| USA | 0.316 | 0.591 | 0.108 | 0.077 | 0.065 |
* indicates rejection of the null hypothesis θ = Θ at the five per cent level of significance. |
|||||
The role of the exchange rate regime in determining the optimal degree of wage indexation can be illustrated by comparing, for example, Canada and France. As shown in Table 3, the variance of demand shocks (relative to supply) is relatively greater in France. This would tend to make Θ larger for France than for Canada. However, the Canadian nominal exchange rate is the more flexible of the two (α = 0.137 for Canada versus α = 2.250 for France). The difference in exchange rate regimes offsets the effects of the relative shocks and so the estimated value of Θ is about the same for both countries.
A comparison of the first and third columns of Table 4 shows that in only one country, Austria, did the actual degree of wage indexation exceed the optimum value. In all the other countries, Θ exceeded θ, in many cases by a considerable margin. This implies an excess demand for labour. How can this result be reconciled with the high and generally increasing unemployment that was observed in these countries over the sample period?
To answer this question one should remember that the estimated values of θ and Θ refer to the indexation of the innovations of wages to prices; nothing has been said about the indexation of anticipated wages to prices. It is possible that real wages in each country were set at the wrong level at the initiation of each wage contract, with wages thereafter being indexed at a rate equal to, or less than, the optimal rate. In this case, classical unemployment (due to real wages being above their market-clearing levels) would still exist, but to a lesser extent than if the degree of indexation exceeded its optimum.
This explanation is consistent with a high level of unemployment. However, it is inconsistent with unemployment levels that are both high and increasing, unless one is willing to entertain the notion that wage setters continually make, and compound, the same miscalculations in determining real wages. These errors would take the form of perpetually setting a real wage level at the beginning of each contract, that is not just excessively high, but increasingly so over time.
A more attractive explanation is that increases in unemployment in these countries were a result of hysteretic effects in the labour market. The idea is essentially that an increase in unemployment propagates itself long after the dissipation of the initial cause of that unemployment, due to such effects as depreciation of the human capital of the long-term unemployed. This train of events might be initiated by an adverse shock (e.g. an oil shock) which lowers the equilibrium real wage. If, following this shock, the actual real wage is not reduced sufficiently, an initial rise in unemployment will result. Even if wages are indexed at rates less than or equal to the optimum thereafter, hysteretic effects will cause continued high (and increasing) unemployment.[16]
The hypothesis of optimal wage indexation is formally tested by constructing the Wald statistic:
which is distributed as Chi-square1.[17]
The Wald statistics in Table 3 show that only for Canada and France can the hypothesis of optimal wage indexation be formally rejected. Nevertheless, for all countries, except Austria, Θ appears to be significantly less than θ in an economic sense. There is no evidence, therefore, to support the existence of an “excessive” degree of wage indexation in the major industrial countries over the period 1973 to 1988, given the stance of monetary policy. A corollary to this conclusion is that there is no evidence to suggest that the exchange rate regime (by way of innovations to the growth of the money supply) was insufficiently accommodating to permit real wages to realize their equilibrium levels.
Footnotes
Blanchard and Summers (1986) provide evidence that hysteresis is an important cause of European unemployment. [16]
To construct the statistic W, one needs to assume a value for cov(θ,Θ), (I assume it is equal to zero) and to calculate the variance of the non-linear term Θ. Linearizing Θ by a Taylor expansion, its variance is obtained as a linear function of the variances of the estimated parameters and shocks. The details of this calculation can be found in Appendix 3. [17]