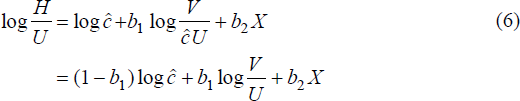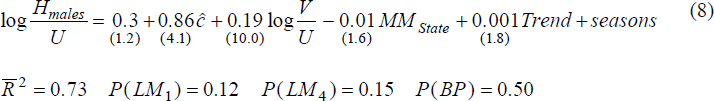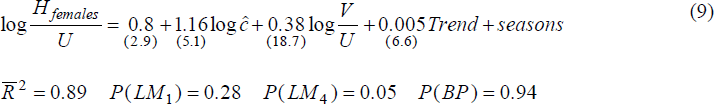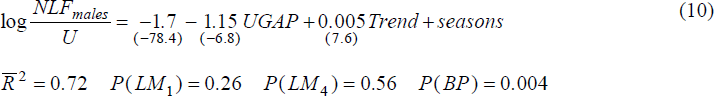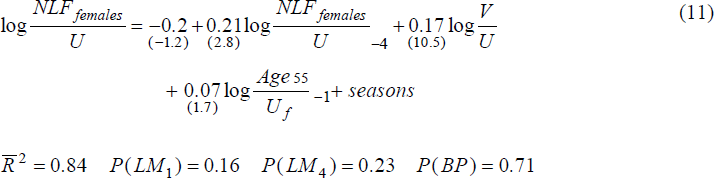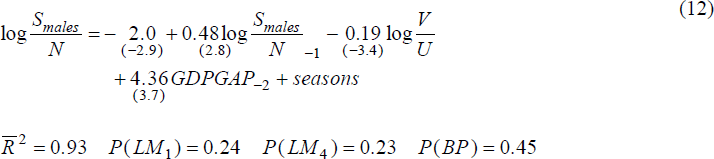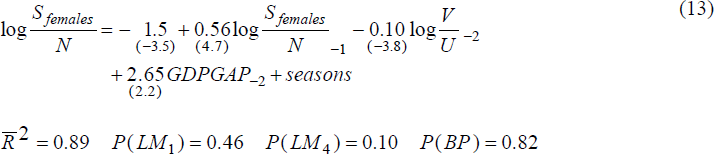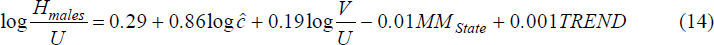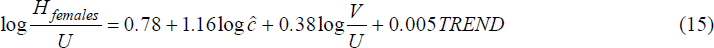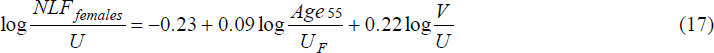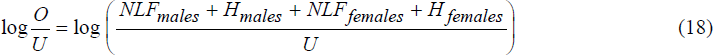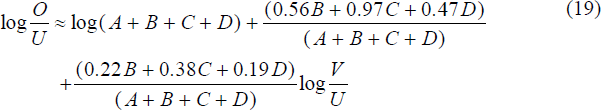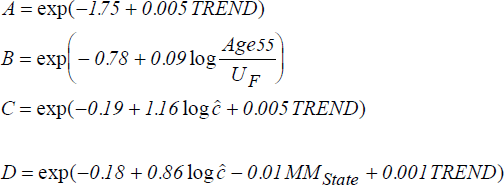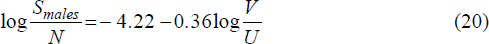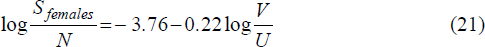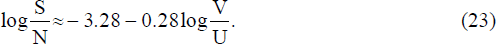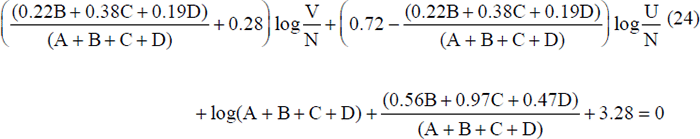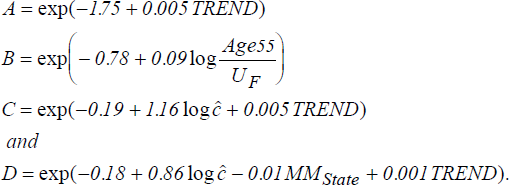RDP 9305: The Unemployment/Vacancy Relationship in Australia 4. An Equilibrium Model of the UV Relationship
June 1993
- Download the Paper 120KB
Our model of the equilibrium Beveridge Curve is an extension of the work of Layard et al. (1991), who estimate this relationship for the United Kingdom. As far as application to Australia is concerned, the Layard model is deficient in two respects: it excludes women, and it assumes that all exits from unemployment are to employment. These distinctions are important because men and women behave quite differently in the Australian labour market; the flow from unemployment to outside the labour force is especially important for women. Our extensions to this model are thus to separately estimate the entry to, and exit from unemployment of men and women, and to separately estimate the exit from unemployment to employment, and to outside the labour force. We then aggregate these estimates to derive an equilibrium Beveridge Curve for the economy as a whole[5].
4.1 Outflows from Unemployment
We begin by considering the outflow from unemployment. Outflows from unemployment to employment are based on the hiring function:
The number of hirings per period (H) depends on the number of vacancies (V), the number of unemployed people (U), and their average effectiveness at searching for work, c. Thus hirings are affected not only by the number of vacancies and unemployed, but also by the behaviour of the unemployed. The number of hirings will rise as the unemployed, on average, become more effective job seekers.
The search effectiveness of the unemployed is determined by factors such as the level and availability of unemployment benefits, the time and effort the unemployed devote to job search, and the recruitment practices of employers. In particular, the search effectiveness of the unemployed is determined by the duration of unemployment. This operates through two mechanisms. Long-term unemployment is used as a screening device by employers, with the probability of being hired falling as the length of an unemployment spell increases. Secondly, long duration unemployment demoralises the individual, and leads to an erosion of their job skills. This explanation is referred to as ‘duration dependence’ because the declining exit rates from unemployment are a function of the duration of the unemployment spell.
Of course it may be the case that exit rates fall with duration because the ‘best’ job seekers find employment first. New entrants to unemployment are heterogeneous in the sense that they, ex-ante, vary in quality in terms of job skills, motivation, attachment to the labour force etc. Thus, exit rates for a heterogeneous group will decline with duration simply because the ‘best’ individuals will exit most rapidly.
However, most of the available evidence favours duration dependence. Layard et al. (1991) cite evidence from British and USA studies which find adverse effects on motivation, morale and psychological health from extended periods of unemployment. They also present their own findings based on a comparison of the exit rate for new entrants compared with the overall exit rate. Under pure heterogeneity the ratio of the exit rate for new entrants to the aggregate exit rate should be constant over time. This is because the proportion of enthusiastic and unenthusiastic job seekers in the stock and in the inflow to unemployment will remain constant regardless of the state of the labour market. Layard et al. found that between 1969 and 1985 the overall exit rate fell by five-sixths, while the exit rate of new entrants fell by only just over one-half [6],[7].
As search effectiveness is primarily a function of the duration of unemployment, we measure it using the following index:
where hd0 is the exit rate at each uncompleted duration
(d) in any arbitrarily selected year 0, while fdt is the
proportion of unemployed at that duration in year t. A rise in
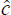 implies an increase in unemployment
effectiveness since a higher proportion of the unemployed are in short durations
which have a higher exit probability.
implies an increase in unemployment
effectiveness since a higher proportion of the unemployed are in short durations
which have a higher exit probability.
The number of effective job seekers is cU. H(·) is assumed to be linearly homogeneous in V and cU. Thus both sides of equation (3) can be divided by cU:
Expressing the hiring function in log-linear form and substituting in
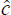 gives:
gives:
where H is hires, i.e. the number of unemployed, during each quarter, who find employment, and X is a vector of other variables which affect hires out of unemployment.
We estimated equation (6) separately for males and females, and in doing so experimented with many different explanatory variables in the regressor set X. These variables were:
- the replacement ratios for males and for all beneficiaries;
- the output gap;
- measures of state and industry mismatch;
- a time trend; and
- seasonal dummies.
We would expect the replacement ratios and mismatch indices to have a negative effect on hires, and the output gap to have a positive effect[8]. The Data Appendix contains a detailed explanation of how these variables are constructed.
We also estimated exits from unemployment to outside the labour force, with equations of the form:
where NLF males is the number of men exiting unemployment by leaving the workforce, and similarly for NLF females. The regressor set X included the same variables as enter the hires equations, and also other variables which might affect labour force participation. These were:
- the proportion of the unemployed aged over 55;
- the unemployment gap, calculated as the difference between actual and (Hodrick-Prescott) trend rates of unemployment;
- the proportion of the unemployed who have been so for more than one year (the long term unemployed); and
- the share of part-time employment in total employment.
Each of these variables, except the unemployment gap, might be expected to be positively correlated with the rate of exit from unemployment to outside the labour force. A rise in unemployment above trend, on the other hand, is generally accompanied by an influx of newly unemployed, highly committed job seekers who will have an above-average attachment to the labour force. Therefore when the unemployment gap rises, the proportion of the unemployed leaving the labour force should fall.
Our preferred equations are presented below. The sample period is 1979(4) to 1992(1), and the estimation method is by instrumental variables because, by construction, the UV ratio is correlated with each equation's disturbance term[9].
where P(BP) is the marginal significance level for the Breusch-Pagan test for heteroskedasticity. U is the total number of unemployed, i.e. male and female. We use total unemployment in the outflow equations as this makes possible the derivation of the aggregate equilibrium Beveridge Curve; see sub-section 4.3 below. The numbers in parentheses are t-statistics.
The BP test shows the likely presence of heteroskedasticity in equation (10), and so implied standard errors reported here are those consistently estimated by the Newey-West procedure.
The effectiveness index is robustly estimated for both hiring equations, as is the vacancies to unemployment ratio[10]. However, most of the additional explanatory variables do not fare as well. In no case was the coefficient on the replacement ratio significantly different from zero; likewise for industry mismatch. Regional (state) mismatch does appear in the hiring equation for males, albeit only at the 12 per cent signficance level.
The failure of the replacement ratio to exert a significant effect on outflows is somewhat surprising, given its prominence in the literature. However, this failure might be explained by specific institutional features of the Australian benefit system (e.g. loss of entitlement following refusal of a job offer) or by tightened eligibility criteria and stricter application of the work search test[11]. It also accords with the findings of Trivedi and Baker (1985) and McMahon and Robinson (1984). Moreover, as pointed out by Atkinson and Micklewright (1991) in their extensive review of unemployment compensation and labour market transition, unemployment benefits impart both an income effect and substitution effect on job search. While the latter leads to less search, the income effect of higher unemployment benefits leads to more search, not less, since job search is generally costly. Perhaps the insignificance of the replacement ratio in our outflow equations is due to these two effects offsetting each other.
This result might also be due to our relatively short sample period. Figure 4 plots the unemployment rate for all persons against the replacement ratio for adult males[12]. It is apparent that during the mid 1970s the large rise in the unemployment rate was accompanied by a significant increase in the replacement ratio. However, between December 1979 and March 1992 (the period over which the outflow equations are estimated), there was no such correlation. Possibly, were we to have gross flow data over the time period depicted in Figure 4, we would find outflows to be affected by the replacement ratio.
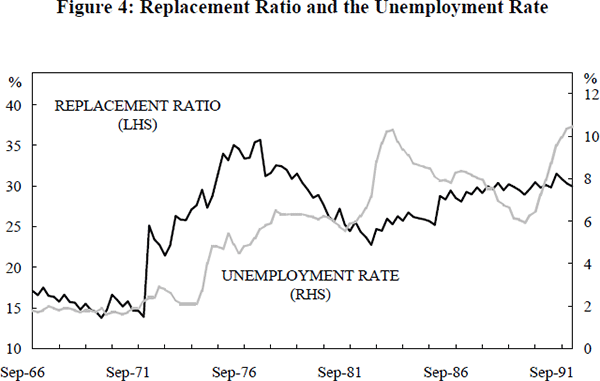
Another possibility is that job search depends not on the value of unemployment benefits, but on the maximum length of time that such benefits can be received. This hypothesis cannot be tested with Australian data since unemployment benefits have always been receivable for unlimited periods of time.
In summary, we can conclude from the outflow equations for the 1980s that:
- there is no evidence that the increase in the proportion of males leaving unemployment by exiting the labour force is related to mismatch, long duration unemployment or age. A rise in cyclical unemployment leads to fewer exits; however, by construction, this variable cannot explain exits (and consequently the UV relationship) in the long run.
- the slight trend rise in male hires has been more than offset by falls in the search effectiveness index and the rise in regional UV mismatch;
- female exits from unemployment to outside the labour force are positively related to vacancies, which may indicate an added worker effect, i.e. married women enter (leave) the labour force in order to stabilise family incomes in response to falling (rising) labour demand. There is also a positive association between vacancies and the proportion of unemployed females aged over 55; and
- there is no relationship between the outflow rates of males or females and the replacement ratio. Nor, it appears, does UV mismatch by industry affect outflow. There is some evidence that mismatch by state affects male hires.
4.2 Inflows to Unemployment
We specifiy inflows simply as a function of the UV ratio, the replacement ratio, the output gap and a time trend.
The estimated equations describing the inflows to unemployment are:
and
where S represents inflows to unemployment and N is the (aggregate) labour force.
Thus, for both men and women, inflows to unemployment increase when the ratio of vacancies to the numbers of unemployed falls, and when output is below trend. Neither of these results is surprising. We are also unable to detect a trend in either of the inflow equations.
4.3 Derivation of the Equilibrium UV Relationship
To derive the equilibrium Beveridge Curve, we equate aggregate long run outflows and inflows. The four long-run outflow relationships are:[13]
Aggregate outflows are:
which is clearly non-linear in the explanatory variables. Since we need to obtain a linear relationship in log (V/U) to derive the equilibrium Beveridge Curve, we linearise equation (18) by a Taylor series expansion around the mean value of log (V/U) over the sample period. The linearised expression is:
where:
Over the sample period the coefficient on log(V/U) is in the range 0.208 to 0.213, with a mean value of 0.210.
The accuracy of this linearisation can be gauged from Figure 5, which plots the nonlinear and linear aggregate outflow equations. Clearly, the linear expression is an accurate approximation of the non-linear equation; the Root Mean Squared Percentage Error is only 0.7 per cent.
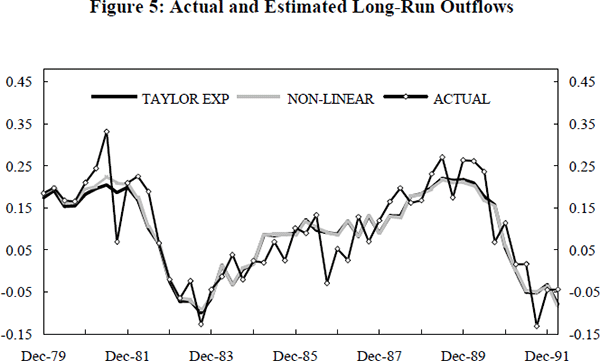
Figure 5 also provides some (weak) evidence of hysteresis operating through the outflows from unemployment. In large downturns, such as in 1982–83 and 1990–91, the equilibrium outflow rate followed the actual rate downwards. However, during the mild downturn of 1986–87 the equilibrium outflow rate stayed constant while the actual rate fell.
The long run inflow equations for males and females are:
Aggregate inflows are therefore:
which is also non-linear in the explanatory variables. The Taylor series expansion around log(V/U) is:
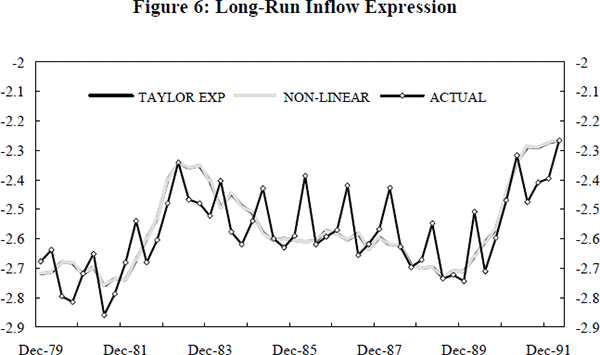
The accuracy of this linear approximation can be seen in Figure 6. There is no visible difference between the non-linear expression and its linearised form, with the RMSE only 0.09 per cent.
The steady state relationship between U and V is derived by equating logO and logS from equations (19) and (23):
where, once again:
Equation (24) is a complex expression from which it is not easy to discern the factors which shifted the Beveridge Curve. Using annual average data it is possible, however, to construct an equilibrium Beveridge Curve for each year from 1980 to 1991. In Figure 7 the equilibrium UV curves are plotted for 1980 and 1989. These two years are chosen for comparison, as with unemployment rates of 5.4 per cent and 5.8 per cent respectively (based on gross flow data), one might consider these to be years where the unemployment rate was close to its equilibrium. Figure 7 indicates that there has been a small outward movement of the UV curve.
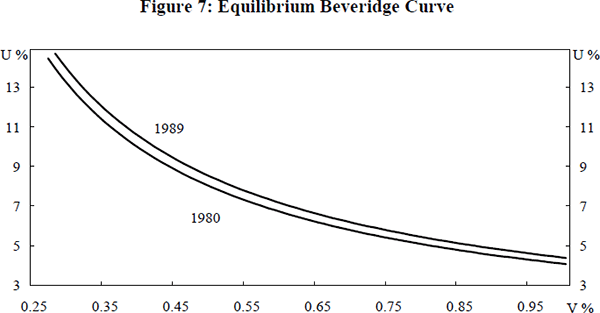
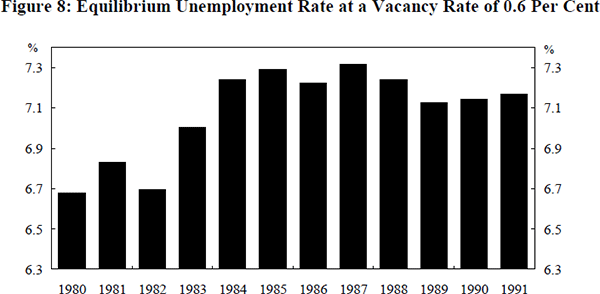
Figure 8 plots the equilibrium unemployment rate for each year coinciding with a vacancy rate of 0.6 per cent. This is the average vacancy rate over the sample period. By holding vacancies constant, Figure 8 illustrates the movement of the Beveridge Curve in each year. It is clear that most of the outward movement of the curve occurred in 1983 and 1984, and that the curve has only shifted back marginally since peaking in 1987[14].
To identify the forces driving the movement in the curve we need to look more closely at the inflow and the outflow equations.
From equation (23) we know that aggregate inflows are influenced only by vacancies and unemployment. As a result the factors which influence the outflow equations must also be the only ones influencing the position of the equilibrium Beveridge Curve.
Equations (14) and (15), describing the outflow from unemployment to employment for
males and females attribute a very large role to the index of search effectiveness
of the unemployed,
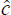 .
Figure A2 shows that
.
Figure A2 shows that
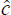 fell considerably over the 1980s as a result of the rise in long-term unemployment.
In fact, the fall in
fell considerably over the 1980s as a result of the rise in long-term unemployment.
In fact, the fall in
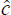 can be identified as the major cause of the outward shift of the Beveridge Curve.
Offsetting the effect of
can be identified as the major cause of the outward shift of the Beveridge Curve.
Offsetting the effect of
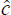 on the curve is the positive time trend in some of the outflow equations, which
has moved the Beveridge Curve towards the origin. The time trend explaining
male hires has only a small weight in the aggregate outflow equation, while
the time trends explaining female hires and male exits from unemployment to
out of the labour force are relatively important. The former possibly reflects
the secularly increasing likelihood of unemployed women finding part-time jobs,
due to the changing sectoral structure of the
workforce[15].
The latter probably represents declining male labour force participation in
the 1980s.
on the curve is the positive time trend in some of the outflow equations, which
has moved the Beveridge Curve towards the origin. The time trend explaining
male hires has only a small weight in the aggregate outflow equation, while
the time trends explaining female hires and male exits from unemployment to
out of the labour force are relatively important. The former possibly reflects
the secularly increasing likelihood of unemployed women finding part-time jobs,
due to the changing sectoral structure of the
workforce[15].
The latter probably represents declining male labour force participation in
the 1980s.
Regional mismatch and the proportion of unemployed females aged over 55 also affect the position of the UV curve. Figure A3 does not provide any clear evidence of a long-term upwards trend in regional UV mismatch, with mismatch increasing during economic downturns and then returning to its previous level. There is also no evidence of a trend increase in the proportion of unemployed females aged over fifty-five.
Finally, we note that the existence of an equilibrium Beveridge Curve implies that equilibrium in the labour market is two dimensional. There is a range of possible ‘equilibrium’ rates of unemployment, each associated with a vacancy rate. Each point on the UV loci describes a situation where inflows equal outflows. However, the particular UV combination which corresponds to the NAIRU will be determined primarily by the wage bargaining process. A complete analysis of labour market equilibrium therefore requires an examination of not just wage setting and unemployment (the traditional Phillips Curve approach) but also of vacancies and unemployment. Research along these lines has been conducted recently by Blanchard (1989) and Jackman, Pissarides, and Savouri (1990).
Footnotes
Separate Beveridge Curves for men and women cannot be estimated because the vacancy data are not gender specific; indeed anti-discrimination laws now prohibit the advertising of vacant positions by gender. [5]
Due to data limitations we were unable to perform a similar test. However, Trivedi and Hui (1988) using gross flow data find evidence of negative duration dependence for long-term unemployed in Australia. [6]
See also Jackman and Layard (1991). [7]
It may be the case that there is some correlation between some of these explanatory
variables and
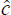 . In particular
. In particular
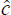 may be related to the replacement
ratio and the measures of UV mismatch. A sustained rise in UV mismatch could
lead to falling exit rates. However, cross correlations show no collinearity
between state mismatch and
may be related to the replacement
ratio and the measures of UV mismatch. A sustained rise in UV mismatch could
lead to falling exit rates. However, cross correlations show no collinearity
between state mismatch and
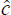 , and only slight correlation between
industry mismatch and
, and only slight correlation between
industry mismatch and
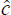 . Furthermore, the plots of
. Furthermore, the plots of
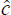 and industry mismatch in Figures
A2 and A3 indicate that there is no long term relationship between the two
series.
[8]
and industry mismatch in Figures
A2 and A3 indicate that there is no long term relationship between the two
series.
[8]
With the exception of
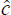 , lags of the contemporaneous regressors
are used as instruments.
, lags of the contemporaneous regressors
are used as instruments.
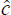 does not have an instrument. Random
shocks to the outflow rate will, in expectation, be uncorrelated with
does not have an instrument. Random
shocks to the outflow rate will, in expectation, be uncorrelated with
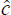 .
[9]
.
[9]
The hypothesis of linear homogeneity, i.e. that the sum of the coefficients on the effectiveness index and UV ratio sum to one, is easily accepted for male hires. [10]
In their 1991 annual report, the Department of Social Security claimed that the number of reviews of pension and benefit entitlements doubled between 1988–89 and 1990–91. [11]
The construction of the replacement ratio is discussed in the Data Appendix. [12]
Additive seasonal dummy variables were used in estimating the inflow and outflow equations. As a result the constants in the long-run equations are calculated as a simple annual average of the value the constant takes in each quarter. [13]
Figure 8 suggests that the position of the Beveridge Curve remained constant in 1990
and 1991. In fact, the results from estimation indicate that the curve shifted
back towards the origin over these two years. This apparent inward shift
of the curve is entirely due to a large measured rise in the effectiveness
index beginning in 1990, which can be attributed to the sudden influx of
newly unemployed (see the Data Appendix
for a more detailed explanation). The resulting inward shift of the curve is therefore
entirely misleading. The unemployment rates for 1990 and 1991 in Figure 8
have been generated by adjusting
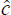 to remove the large apparent, but
spurious, rise in search effectiveness beginning in 1990.
[14]
to remove the large apparent, but
spurious, rise in search effectiveness beginning in 1990.
[14]
Fahrer and Heath (1992) examine this development in detail. [15]