RDP 9307: Explaining Forward Discount Bias: Is it Anchoring? 3. Anchoring as an Explanation

To motivate the formal modelling to follow, here we describe how the presence of anchored traders can explain the foreign exchange puzzles described above. We consider a world like the one described by Dornbusch (1976) and make the following assumptions.

Model Assumptions:

There are two open economies, domestic and foreign, with a market-determined exchange rate between them. The foreign goods-price level is constant through time as is the foreign interest rate. The domestic economy is small in the world capital market and so takes the foreign interest rate as given. In the domestic economy, output is fixed and there is no trend money growth and no trend inflation but goods prices adjust slowly to money supply shocks. The domestic interest rate on short-term nominal assets clears the domestic money market and satisfies an international arbitrage condition. Finally, there is a forward market for foreign exchange with no default risk and no transaction costs so covered interest parity holds at all times,

where s_t and f_t are the time t log spot price of foreign exchange and 1-period forward rate respectively, fd_t is the 1-period forward discount and i_t and i^* are the one period interest rates on domestic and foreign nominal assets.^[11]

We now compare the market reaction to a single unanticipated domestic monetary expansion when all foreign exchange traders are rational with the reaction when they are all anchored to the forward rate. To ease exposition, we assume all traders are risk-neutral, while in the formal model in the next section, we assume (for a reason that will become clear) that they are risk-averse. Before the monetary expansion, goods prices and the nominal exchange rate are in long-run equilibrium.

That is, s_t = ₀ where ₀ is the (initial) long-run equilibrium level of the spot rate (see Figure 2). In this equilibrium, the risk-neutral foreign exchange agents ensure that domestic and foreign interest rates are equal (i_t = i*).^[12]

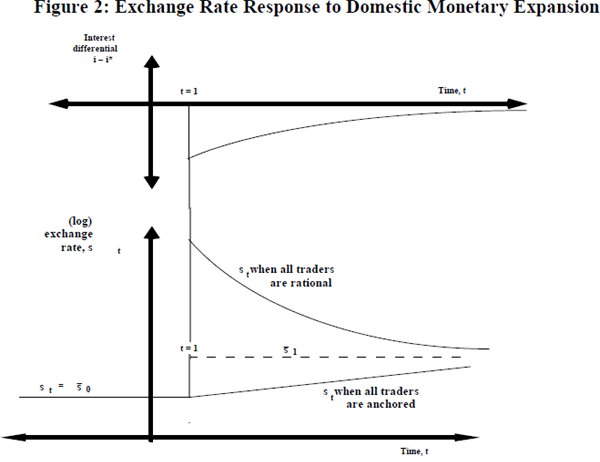
It helps to imagine the events surrounding the monetary expansion as occuring in two sequential stages. At the first stage, at , the monetary expansion occurs, the domestic interest rate falls to clear the domestic money market and the forward rate moves to satisfy covered interest parity, but the spot rate remains unchanged i.e., s₁ = ₀. At the second stage, at , the foreign exchange market equilibrates. In general, the second stage involves movement of the spot rate, the forward rate and the domestic interest rate.^[13] Note, however, that whatever movement of the spot rate is required to equilibrate the market, riskless arbitrage ensures that covered interest parity always holds.

While the first stage of this process is the same whether traders are rational or anchored, the second stage is not. As Dornbusch showed, with rational traders, the nominal exchange rate eventually fully reflects the monetary expansion but it initially overshoots (see Figure 2). To stress a key point: at t = 1⁺ a spot rate s₁₊ = ₀ is not consistent with market equilibrium because rational traders are aware of an excess return to be earned on the foreign asset at this spot rate. Rational traders' realisation of this excess return drives the spot rate onto its overshooting path.

Now assume that, rather than understanding their economic environment, all traders' expectation of the one-period-ahead spot rate is simply equal to the current 1-period forward rate. Now, at t = 1⁺, these anchored traders have no reason to drive the exchange rate onto the overshooting path because they are unaware of the excess return to be earned on the foreign asset.^[14]

That much is clear. But, by itself, this argument does not determine either the level of the spot rate at t = 1⁺ nor how it evolves to a new long-run. An auxiliary assumption is needed. The assumption we invoke is that, as well as being anchored to the forward rate, these traders have a target level for the real exchange rate. Then, in a market inhabited exclusively by such traders, there is no initial jump in the spot rate (s₁₊ = ₀) and it gradually adjusts to long-run neutrality . This ‘anchored’ adjustment path is shown in Figure 2.^[15]

One point deserves emphasis. Our explanation of the anchored traders' behaviour does not rely on fleeting irrationality in the instant following a monetary expansion. There is nothing special about that instant. All along the ‘anchored’ path, there is an excess return to holding the foreign asset but traders who use the forward rate as their expectation of the one-period-ahead spot rate are unaware of this excess return and hence never set off a Dornbusch-style overshooting adjustment.

What are the implications for the regressions (1) and (2)? With the foreign exchange market composed entirely of rational traders, both the expected exchange rate change and the actual exchange rate change are equal to the forward discount along the adjustment path. By contrast, with the foreign exchange market composed entirely of anchored traders, the expected exchange rate change is again equal to the forward discount, but the actual exchange rate change is in the opposite direction to the prediction of the forward discount (b in equation (1) is negative).

Thus, if the foreign exchange market is composed entirely of anchored traders, this simple story predicts that b < 0 and d = 1, as the empirical results in Section 2 suggest. This is a promising step, but it cannot be the whole story.

Firstly, if exchange rates adjusted smoothly and gradually to money shocks as in Figure 2, anchored traders would presumably learn that their expectations were systematically and repeatedly wrong. It strains credulity to argue that such expectations could survive in such circumstances. But, as discussed in the introduction and as highlighted in Figure 1, nominal exchange rates are subject to continual unpredictable shocks which are very much larger than (and uncorrelated with) the forward discount. In such an environment, it is not so implausible that some participants in the foreign exchange market are subject to a small psychologically-based bias in their exchange rate expectations.

Secondly, the foreign exchange market cannot be composed entirely of anchored traders. The bias of the forward discount has been well-established for at least a decade, and there are obviously participants in the market who can exploit it. Can the simple explanation presented above survive the presence of rational traders who are aware of the forward discount bias? The next section tackles this question.

Footnotes

Throughout, lowercase variables with the exception of interest rates are the logs of corresponding uppercase variables and foreign variables are denoted with a star. [11]

Although it is not clear at this stage, readers should take as given that the long-run equilibrium is the same whatever the nature of the foreign exchange traders. [12]

In a standard specification, movement of the spot rate affects the domestic price of imports, hence the domestic goods price level, hence the level of real balances and the domestic interest rate. [13]

These traders' expected nominal return on the foreign asset (measured in domestic currency) is i^* + (f₁+ − s₁+) while the nominal return on the domestic asset is i₁+. Whatever the value of s₁+, covered interest parity ensures that these expected returns are equal. Note that, rather than being anchored to the forward rate, one can interpret these traders as being ‘anchored’ to a simple form of the efficient markets hypothesis so that they are again unaware of the excess return to be earned on the foreign asset. This interpretation was suggested by Avinash Dixit. [14]

All along this path, the real exchange rate is equal to the anchored traders' target and their expectation of the one-period-ahead spot rate is equal to the forward rate. A formal derivation of this adjustment path is presented in Section 4.6. One final clarifying point. As discussed earlier, the interest differential depends on the behaviour of the exchange rate. To avoid unnecessary clutter, Figure 2 ignores this dependence and shows a single path for the interest differential. [15]