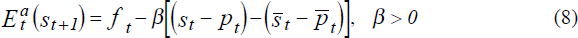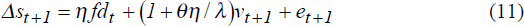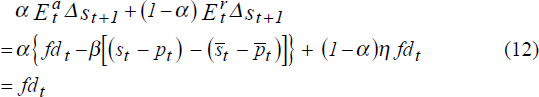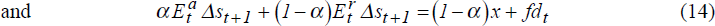RDP 9307: Explaining Forward Discount Bias: Is it Anchoring? 4. A Model with Anchored and Rational Traders
June 1993
- Download the Paper 119KB
There are two features of the floating exchange rate environment we want to capture in a model. These features are the strong autocorrelation in short-term nominal interest differentials between countries and the very large unpredictable shocks to the nominal and real exchange rate. We model the former feature by assuming sticky goods-prices, so in response to nominal money shocks, the domestic-foreign nominal interest differential adjusts slowly back to long-run equilibrium. Following Campbell and Clarida (1987), the latter feature is modelled by assuming that the long-run real exchange rate follows a random-walk.[16] Beyond capturing these features of the exchange rate environment, our model is as simple and stripped-down as possible.
The model is a two-country model in discrete time, with each period of four weeks duration. The government in each country issues local-currency-denominated interest-bearing nominal assets with a maturity of one period. The foreign exchange market contains two types of mean-variance optimising traders: rational and anchored. A fraction α of market wealth is managed by the anchored traders with 1 – α managed by the rational traders. For the moment α is specified exogenously, but in Section 5 it will be determined endogenously.
4.1 The Stochastic Environment in the Foreign Exchange Market
The stochastic properties of goods-price adjustment and the domestic-foreign interest differential are derived as follows. We make the Model Assumptions (defined in Section 3) and also assume for the domestic economy that the money market has a standard LM curve, that the money supply is subject to independent shocks each period and that aggregate demand is a simplified version of the Dornbusch (1976) form. These assumptions lead to three reduced-form equations:
where, in period t, pt and
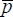 t are logs of the
domestic goods price level and its long-run equilibrium, (i−i*)t
is the interest differential between domestic and foreign one-period nominal
assets, and νt is an i.i.d. N (O,
t are logs of the
domestic goods price level and its long-run equilibrium, (i−i*)t
is the interest differential between domestic and foreign one-period nominal
assets, and νt is an i.i.d. N (O,
 ) shock to the log domestic money supply.
λ is the semi-elasticity of money demand with respect to the interest
rate and 1/θ is the rate at which goods prices, and hence the domestic-foreign
interest differential, adjust to money shocks.
) shock to the log domestic money supply.
λ is the semi-elasticity of money demand with respect to the interest
rate and 1/θ is the rate at which goods prices, and hence the domestic-foreign
interest differential, adjust to money shocks.
Long-run neutrality implies equation (4) while (5) and (6) are derived in Appendix A. Here, we explain our use of a simplified form of the Dornbusch (1976) domestic demand function. Dornbusch assumes that demand depends on real income, the interest rate and the real exchange rate. We drop the dependence on the real exchange rate and as a consequence, must impose a constraint between exogenous variables in the model (see Appendix A). This greatly eases analysis of the stochastic environment in the foreign exchange market and allows the rational-expectation solution for the exchange rate to be derived straightforwardly. Crucially, the key features of the Dornbusch model are preserved. That is, in a fully-rational risk-neutral market, the model exhibits both exchange-rate overshooting and the absence of forward discount bias. Finally, we note that equations (5) and (6) are consistent with an arbitrage condition in the foreign exchange market. This arbitrage condition is introduced shortly (equation (10)).
Defining  t as the equilibrium value
of
st (the value of st if there were no
goods-price stickiness) and setting the foreign goods price equal to one, the
equilibrium real exchange rate at time t is
t as the equilibrium value
of
st (the value of st if there were no
goods-price stickiness) and setting the foreign goods price equal to one, the
equilibrium real exchange rate at time t is
 t −
t −
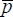 t. We
assume that
t. We
assume that
 t −
t −
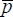 t follows
a random walk
t follows
a random walk
with the shocks et+1 specified
exogenously.[17]
We assume et+1 is distributed i.i.d. N(O,
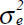 ) on the basis of the observed stochastic
properties of exchange rate changes (see Section 5).
Both the rational and anchored traders are assumed to know the stochastic properties
of these real exchange rate shocks.
) on the basis of the observed stochastic
properties of exchange rate changes (see Section 5).
Both the rational and anchored traders are assumed to know the stochastic properties
of these real exchange rate shocks.
Equations (4) – (7) summarise the stochastic environment in the foreign exchange market. In Section 5, values for the parameters introduced, λ, θ, σm and σe, are derived from data on interest differentials and floating exchange rates.
4.2 The Anchored Traders' Expectations
The anchored traders' expectation of the future exchange rate is given by
This equation embodies two behavioural assumptions:
- the forward rate is an anchor for expectations of the one-period-ahead spot rate, but
- these traders also have a target level of the real exchange rate and if the rate is not at that level, they adjust to expect that it will return back towards that level over time. The parameter β quantifies by how much these traders' expectations adjust (from the anchor) when the exchange rate deviates from their current target level.
Defining the anchored traders' target level in terms of the real exchange rate ensures an appropriate market reaction to both real and nominal shocks as will be shown in Section 4.6.
The second behavioural assumption is crucial. Without it, these traders have no impact on the exchange rate. Thus, if anchored traders' expectations always equal the forward exchange rate, regardless of the value of the current exchange rate, and the market contains even a single rational risk-averse trader, she will drive the exchange rate to a Dornbusch overshooting equilibrium because the rest of the market has no reaction when the spot rate moves.[18]
4.3 The Traders' Asset – Demand Functions
With the wealth entrusted to them by investors, the traders choose the relative proportions
to hold in the domestic and foreign interest-bearing
assets.[19]
Each period, each trader optimises with respect to the mean and variance of the end-of-period
real wealth she manages. By assumption, both rational and anchored traders
have the same coefficient of relative risk aversion, γ, and the same
consumption bundle – which consists of a constant expenditure share g
of foreign goods and (1 – g) of domestic goods. For
trader k, if
 is the proportion of period-t wealth
she holds in the foreign nominal asset, Appendix B
shows that
is the proportion of period-t wealth
she holds in the foreign nominal asset, Appendix B
shows that
Each trader's demand for the foreign asset consists of two terms. The first term, g, is the minimum-variance portfolio. If a trader were infinitely risk-averse (γ = ∞) she would hold this portfolio. The second term represents the ‘speculative’ portfolio. A higher (lower) expected excess return on the foreign asset induces the trader to hold more (less) of that asset than its share in the minimum-variance portfolio, to an extent limited by the trader's risk aversion and the variance of the return.
4.4 The Supply of Domestic and Foreign Interest-Bearing Assets
To simplify the exposition, we describe the solution of the model for the special case in which the supply of domestic and foreign interest-bearing assets made available to be managed by the traders exactly matches their minimum-variance portfolio: that is, of the total wealth managed by the traders, a constant proportion g is in the form of the foreign asset. A more general case, when there is no match, leads to only a small change to the basic story and is dealt with in Section 4.7.
4.5 Determining the Spot Exchange Rate
With the anchored traders managing a proportion α of the total market wealth, equating supply and demand for the foreign asset gives
Equilibrium in the market for the foreign asset ensures equilibrium in the market
for the domestic asset by Walras's Law. Equation (10) leads to a difference
equation in  . Imposing the transversality condition that
. Imposing the transversality condition that
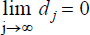 rules out rational bubbles and leads
to the exchange rate change from t to t + 1:
rules out rational bubbles and leads
to the exchange rate change from t to t + 1:
where η ≡ η(α) = 1 − αβ(λ + θ)/(1 + α(βθ −1)) and fdt = (i−i*)t. (Details of the derivation are available from the authors on request.) From equations (8) and (11) we can derive the mean of market participants' exchange rate expectations
It is a striking property of the model that, regardless of parameter values, the mean of market participants' expectations of the exchange rate change is equal to the forward discount. We discuss this result in Section 4.8.
4.6 Market Reaction to Real and Nominal Shocks
Now is a convenient time to show that the model implies an appropriate market reaction to both real and nominal shocks. As can be confirmed from (11), whatever the proportion of anchored traders in the market, the sole effect of a real exchange rate shock, et+1, is to move the spot exchange rate Δst+1 by the amount of the shock. This is the appropriate market reaction since, by assumption, both rational and anchored traders understand the (permanent) nature of real exchange rate shocks.
Now consider the effect of a nominal money shock when the market contains only anchored traders. In this case, there will never be a Dornbusch-style overshooting adjustment because the anchored traders are always unaware of the excess return to be earned on the foreign asset. With only anchored traders in the market and in the absence of further shocks, the time-evolution of the exchange rate in response to a nominal shock νt+1 is st+τ = st + νt+1 [1−(1−1/θ)τ−1], τ≥1 (from (6) and (11)). This time-evolution is simply the ‘anchored’ path in Figure 2. There is no initial jump (Δst+1=0) and the exchange rate adjusts gradually to fully reflect the nominal shock (very gradually, given the numerical estimates of θ from Section 5).
4.7 Relative Asset Supplies Not Equal to the Traders' Minimum-Variance Portfolio
Here we report the solution of the model for the more general case in which the proportion of the total wealth managed by the traders in the form of the foreign asset is g + κ, 0 ≤ g + κ ≤ 1, (rather than g) where g is again the proportion of foreign assets in the traders' minimum-variance portfolio and κ is an arbitrary constant. As shown in Appendix C, the effect of this generalisation is simply to add constants to the right hand sides of equations (11) and (12). The solutions for the exchange rate change and the mean of market participants' exchange rate expectations become
where 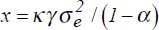 .
.
4.8 Discussion
It is now clear that our explanation of the puzzles described in Section 2 survives the presence of risk-averse rational traders in the market. Equations (13) and (14) are of the same form as (1) and (2), so the model's predictions can be easily compared with the empirical results. In the standard regression for testing the bias of the forward discount ((1), (13)), the model coefficient on the forward discount is η(α) = 1 − (αβ(λ + θ))/(1 + α(βθ − 1)). In a fully-rational market, this coefficient is one (η(0) = 1) and, up to a constant, the forward discount is an unbiased estimate of the future exchange rate change. However, as the proportion of anchored traders in the market rises, η(α) falls monotonically (since ∂η(α)/∂α < 0) taking the value η(1) = −λ/θ when the market is composed entirely of anchored traders.
With both types of trader in the market, the anchored traders make systematic mistakes about the future time path of the exchange rate and the rational traders exploit these mistakes. But because the rational traders are risk-averse, they reduce, but do not eliminate the deviations of the exchange rate from an efficient-market path. Provided there are some anchored traders in the market (α > 0) the forward discount is a systematically biased estimate of the future exchange rate change and the direction of bias is that consistently observed empirically.
Turning now to market expectations, there are two groups with distinctly different expectations. The rational traders have unbiased expectations while the anchored traders' expectations are adjusted from their anchor – the forward exchange rate. But, whatever the proportion of anchored traders, the weighted mean of the traders' expected exchange rate change moves one-for-one with the forward discount (from (14)). Thus, up to a constant, uncovered interest parity holds for average market expectations in the model, despite the fact that no-one in the market has those expectations! Of course, this result for average market expectations accords well with the survey results in Section 2.
Thus, the model can explain both the stylised facts highlighted in Section 2 provided there are some anchored traders in the market in equilibrium. But an important question remains: is it plausible that a sufficient proportion of anchored traders survive in the long-run to generate values of η similar to those consistently observed in foreign exchange markets? The next section addresses this question.
Footnotes
We examine the alternative of modelling these shocks as a stationary AR(1) process at the end of the paper in Appendix F. However, this alternative requires extra complication in the model. [16]
Again, we assume both that these shocks are exogenous and that domestic real output is fixed to keep things simple. As an alternative, we could assume random productivity shocks which have an impact on real output and are the source of the real exchange rate shocks modelled in equation (7). With our focus on the stochastic environment in the foreign exchange market, we did not complicate the model in this way. [17]
It is easy to confirm that the solution of the model (equation (11)) is the same when β = 0 as when there are no anchored traders in the market (α = 0). [18]
There are four assets in the model: money and the interest-bearing asset in each economy. Money is held by individuals in each economy because it provides transaction services.
However, with the wealth entrusted to them by investors, the traders do not hold money because it is a dominated asset.
[19]